深度学习-传统神经网络
神经网络-前向传播
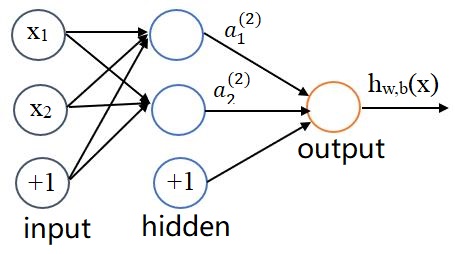
为方便起见只画了一个隐藏层的神经网络,图中的x1,x2也可以是向量,数据从输入层传入,在第一个隐藏层需要经过非线性的激活函数f(z)然后得到a1(2),a2(2),在经过激活函数f(z)得到hw,b(x),具体表示式如下:
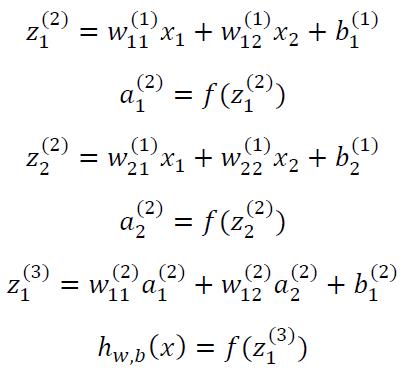
当然还可以用矩阵-向量表示,使表达式看起来更简洁
![]()
注意:f(z)激活函数不止一个,一般常用三个1.Sigmoid,2.tanh 3.ReLU \ Leaky ReLU
具体的公式可以在网上随便翻一下,也可以百度百科,维基百科等,若是懒得找,可以看一下此文https://blog.csdn.net/a493823882/article/details/83543622
反向传播
反响传播的目的是为了调整每一层的参数,使得最后预测或分类的值与实际值尽可能的接近,这时损失函数就出现了,通过损失函数,运用链式法则从后向前一次求出每一层的权值w(参数)具体的可以参照一下https://www.zhihu.com/question/24827633/answer/91489990,当然损失函数还有其它一些选择。至于如何选择,以及损失函数具体的公式可以参见该文章总结的相对详细,它包括用于分类损失函数,用于回归损失函数,和用于生成对抗网络损失函数。
影响深度学习性能最重要因素之一。是外部世界对神经网络模型训练的直接指导,合适的损失函数能够确保深度学习模型收敛。设计合适的损失函数是研究工作的主要内容之一。当然按照损失函数的能力使用所作出的结果一般都很可靠,特殊情况也可以作出相应的改变,用于分类的损失函数也可以试用在回归上等。
自定义损失函数
a. 看中某一个属性
单独将某一些预测值取出或赋予不同大小的参数
b. 合并多个loss
多目标训练任务,设置合理的loss结合方式
c. 神经网络融合
不同神经网络loss结合,共同loss对网络进行训练指导
说到反响传播,就不得不考虑学习率learning_rate这一概念了。神经网络在更新权值w时的公式如下:
w = w - learning_rate * dw,
当学习率很大时可以更快速收敛,而学习率很小时又可以提高精度。但是如何选择更好的学习率呢,如果仅仅是单纯的只对learning_rate调整大小,然后通过比较,看哪个学习率对预测能力影响更大,就可以作出较好的选择,具体的可以看看https://blog.csdn.net/u012193416/article/details/79521508。
当然我们也可以采用动量的方法进行实时调整步长:
v = α * v - learning_rate * dw
W = w + v
其中,v初始化为0,α是设定的一个超变量,最常见的设定值是 0.9。
从式中不难看出如果上次的动量momentum(v)与这次的负梯度方向是相同的,那这次下降的幅度会增加,从而增加收敛。由此可见采用动量的方法改变学习的速度要受到前一次的速度的影响,而直接调整learning_rate,可以说在梯度下降的方向上是没有改变的,也就是说直接调整学习率对于选择最小值来说不太理想,采用动量的方法可以根据上一次的速度有目的的进行调整方向如图:
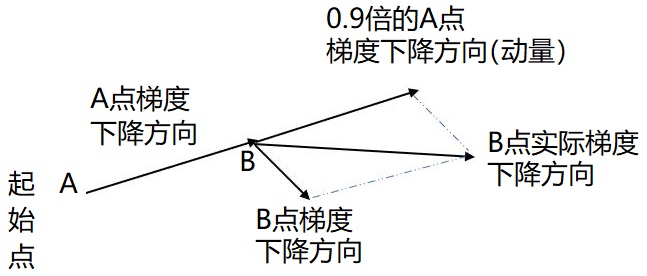
要是当前时刻的梯度与历史时刻梯度方向相似,这种趋势在当前时刻则会加强;要是不同,则当前时刻的梯度方向减弱。
假设每个时刻的梯度g总是类似,那么由我们可以直观的看到每次的步长为:
![]() ,即当设α为0.5,0.9,或者0.99,分别表示最大速度2倍,10倍,100倍于SGD的算法。
,即当设α为0.5,0.9,或者0.99,分别表示最大速度2倍,10倍,100倍于SGD的算法。
过拟合
什么是过拟合以及产生过拟合的根本原因:
https://www.cnblogs.com/eilearn/p/9203186.html
带图的解释https://blog.csdn.net/chen645096127/article/details/78990928
如何防止过拟合https://blog.csdn.net/jadelyw/article/details/80450612
正则项对参数w有什么影响?
答:L2正则项通过约束参数w使其不要太大,在一定程度上缓解过拟合现象。
什么叫做weight decay 与Regularization有何联系?
答:L2正则项也称为权重衰减即 weight decay
Dropout,Pooling区别?
答:Dropout本质是Regularization,Pooling是降维


 浙公网安备 33010602011771号
浙公网安备 33010602011771号