机器学习-概率论与贝叶斯先验-笔记

概率公式

条件概率：

全概率公式：

贝叶斯(Bayes)公式：

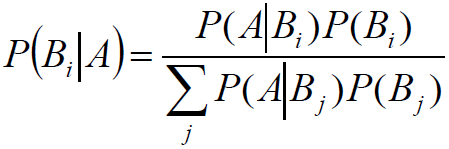
例题：

　　8支步枪中有5支已校准过，3支未校准。一名射手用校准过的枪射击，中靶概率为 0.8用未校准的枪射击，中靶概率为0.3；现从8支枪中随机取一支射击，结果中靶。求该枪是已校准过的概率。

　　解：G=1为校准过的步枪，G=0为未校准过的步枪，A=1表示中靶，A=0表示未中靶

　　

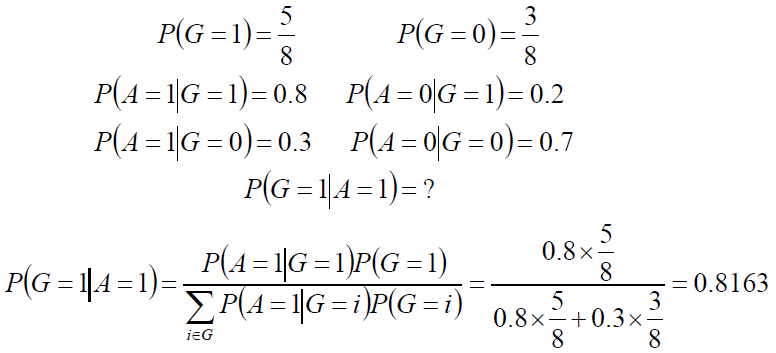
贝叶斯公式

给定某系统的若干样本x，计算该系统的参数，即

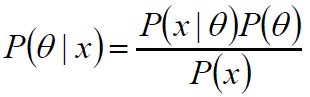
P(θ)：没有数据支持下，θ发生的概率：先验概率。
P(θ|x)：在数据x的支持下，θ发生的概率：后验概率。
P(x|θ)：给定某参数θ的概率分布：似然函数。

分布

两点分布

二项分布Bernoulli distribution

 

 

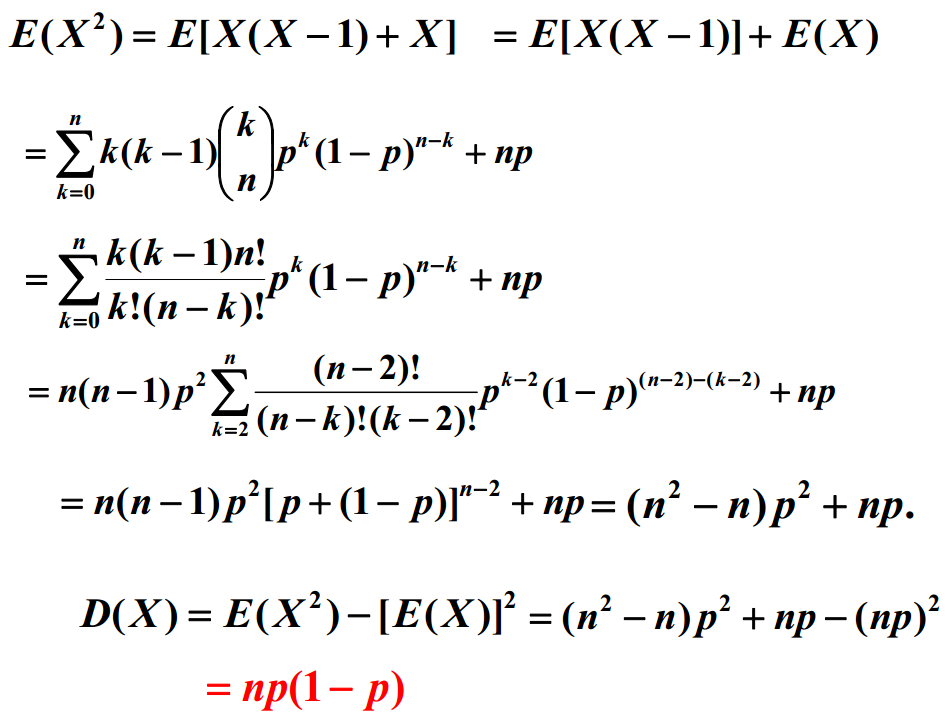
泊松分布

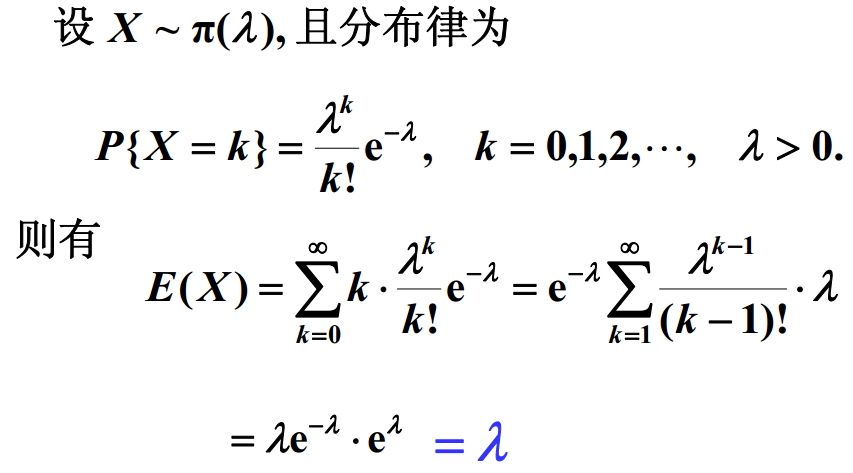
　　在实际事例中，当一个随机事件，以固定的平均瞬时速率 λ( 或称密度随机且独立地出现时，那么这个事件在单位时间面积或体积内出现的次数或个数就近似地服从泊松分布 P(λ) 。

　　某一服务设施在一定时间内到达的人数
　　电话交换机接到呼叫的次数
　　汽车站台的候客人数
　　机器出现的故障数
　　自然灾害发生的次数
　　一块产品上的缺陷数
　　显微镜下单位分区内的细菌分布数
　　某放射性物质单位时间发射出的粒子数

均匀分布

指数分布

 

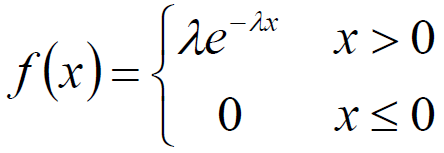
　　其中 λ > 0 是分布的一个参数，常被称为率参数 (rate parameter）。即 每单位时间内发生某事件的次数 。指数分布的区间是 [0,∞)。如果一个随机变量 X 呈指数分布，则可以写作： X~Exponential(λ)。

　　指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、软件更新的时间间隔等等。

　　许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。

指数分布的无记忆性：

　　指数函数的一个重要特征是无记忆性 遗失记忆性， Memoryless Property) 。

　　如果一个随机变量呈指数分布，当 s,t≥0 时有：

　　　　

　　即，如果 x 是某电器元件的寿命，已知元件使用了 s 小时，则共使用至少 s+t 小时的条件概率，与从未使用开始至少使用 t 小时的概率相等。

正态分布

 

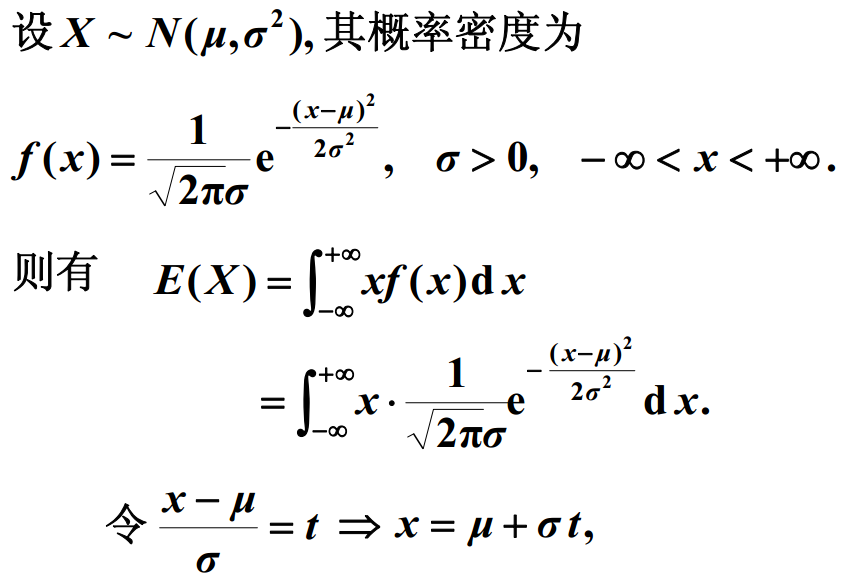
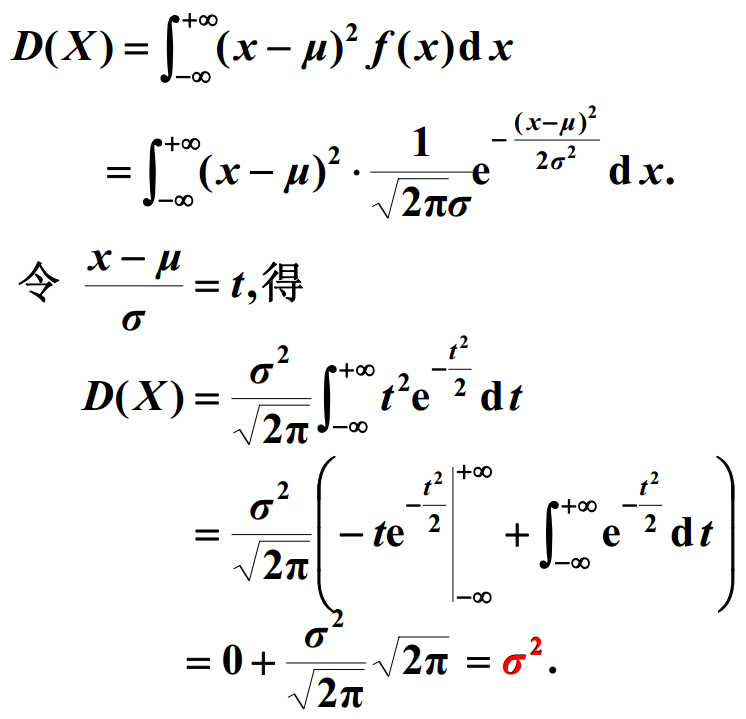
 总结：

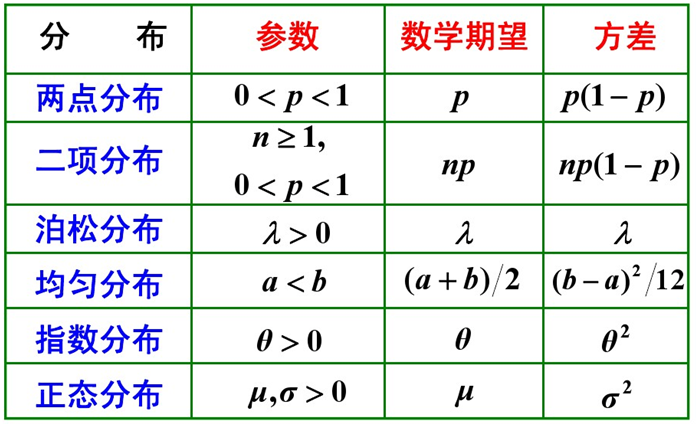
Beta分布

　　Beta分布的期望

　　　　

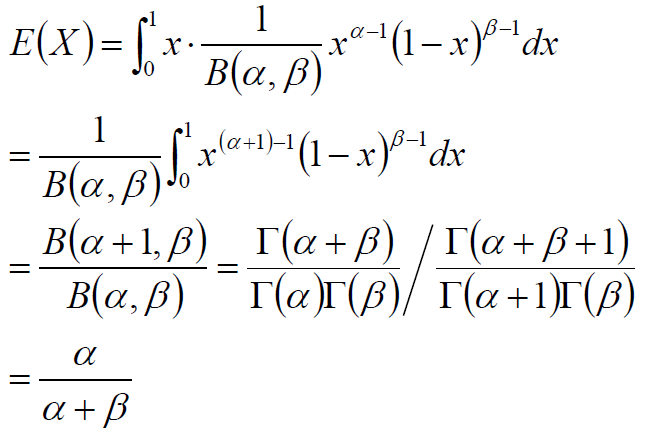
指数族：Bernoulli 分布和高斯分布等

　　Sigmoid函数

　　

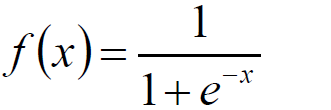
　　Sigmoid函数的导数

　　

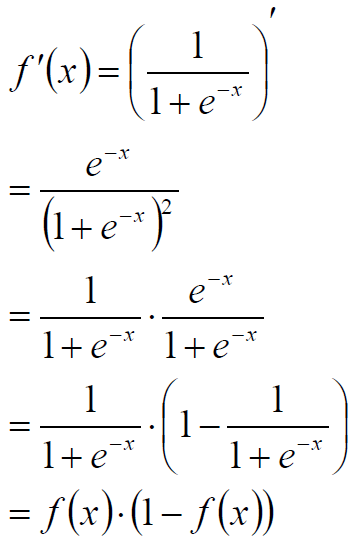
　　Gaussian分布

　　

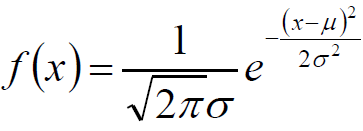
事件的独立性

　　给定A和B是两个事件，若有P(AB)=P(A)P(B)则称事件A和B相互独立。

　　说明：

　　　　A和B独立，则P(A|B)=P(A)

　　实践中往往根据两个事件是否相互影响而判断独立性：如给定M个样本、若干次采样等情形，往往假定它们相互独立。

期望,即：概率加权下的“平均值”

　　离散型

　　

　　连续型

　　

期望的性质

　　无条件成立

　　　　E(kX)=kE(X)

　　　　E(X+Y)=E(X)+E(Y)

　　若X和Y相互独立,则E(XY)=E(X)E(Y)

　　　　反之不成立。事实上，若E(XY)=E(X)E(Y)，只能说明X和Y不相关。

 方差

　　定义: Var(X)=E{[X-E(X)]²}=E(X²)-E²(X)

　　E{X-E(X)2}≥0→E(X²)≥E²(X)当X为定值时，取等号

　　无条件成立:  Var(c)=0

　　　　　　　　Var(X+c)=Var(X)

　　　　　　　　Var(kX)=k²Var(X)

　　X和Y独立：Var(X+Y)=Var(X)+Var(Y)
　　　　此外，方差的平方根，称为标准差

协方差

　　定义: Cov(X,Y)=E{[X-E(X)][Y-E(Y)]}

　　性质： Cov(X,Y)= Cov(Y,X)

　　　　　Cov(aX+b,cY+d)=acCov(X,Y)

　　　　   Cov(X₁+X₂,Y)=Cov(X₁,Y)+Cov(X₂,Y)

　　　　　Cov(X,Y)=E(XY)-E(X)E(Y)

　　协方差和独立、不相关:

　　　　X和Y独立时E(XY)=E(X)E(Y)

　　　　而Cov(X,Y)=E(XY)-E(X)E(Y)，从而，当X和Y独立时，Cov(X,Y)=0

　　　　但X和Y独立这个前提太强，我们定义：若Cov(X,Y)=0, 称X和Y不相关。

　　协方差的意义：

　　　　协方差是两个随机变量具有相同方向变化趋势的度量；

　　　　若 Cov(X,Y)>0，它们的变化趋势相同；

　　　　若 Cov(X,Y)<0，它们的变化趋势相反；

　　　　若 Cov(X,Y)=0，称 X 和 Y 不相关。

　　协方差的上界：

　　　　若   

　　　　则  |Cov(X,Y)|≤σ₁σ₂

　　　　当且仅当X和Y之间有线性关系时，等号成立。

　　　　Cov²(X,Y)=E²{[X-E(X)][Y-E(Y)]} ..............协方差定义

　　　　≤E( ( X-E(X) )² ( Y-E(Y) )² ) .....................方差性质

　　　　≤E( (X-E(X))² )E( (Y-E(Y))² ) ...................期望性质

　　　　=Var(X)Var(Y) .........................................方差定义

　　　　注：第三行“期望性质”的不等号不一定成立，即:E(XY)-E(X)E(Y)符号不定。

　　　　协方差上界定理的证明:

　　　　　　取任意实数t，构造随机变量Z，Z=(X-E(X)).t+(Y-E(Y))

　　　　　　从而:

　　　　　　　　

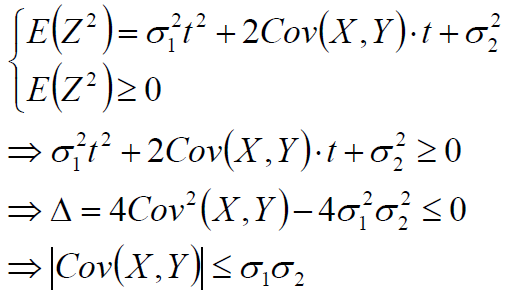
　　再谈独立与不相关:

　　　　因为上述定理的保证，使得“不相关”事实上即“ 二阶独立 ”。

　　　　即：若 X 与 Y 不相关，说明 X 与 Y 之间没有线性关系 但有可能存在其他函数关系 ))，不能保证 X 和 Y 相互独立。

　　　　但对于 二维正态随机变量 X 与 Y 不相关等价于 X 与 Y 相互独立。

Pearson相关系数

　　定义

　　　　　

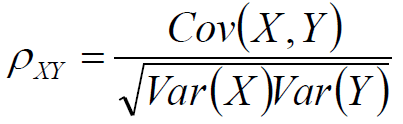
　　由协方差上界定理可知，|ρ|≤1

　　当且仅当X与Y有线性关系时，等号成立

　　容易看到，相关系数是标准尺度下的协方差。上面关于协方差与XY相互关系的结论，完全适用于相关系数和XY的相互关系。

协方差矩阵

　　对于n个随机向量(X₁,X₂…X_n)，任意两个元素X_i和X_j都可以得到一个协方差，从而形成n*n的矩阵；协方差矩阵是对称阵。

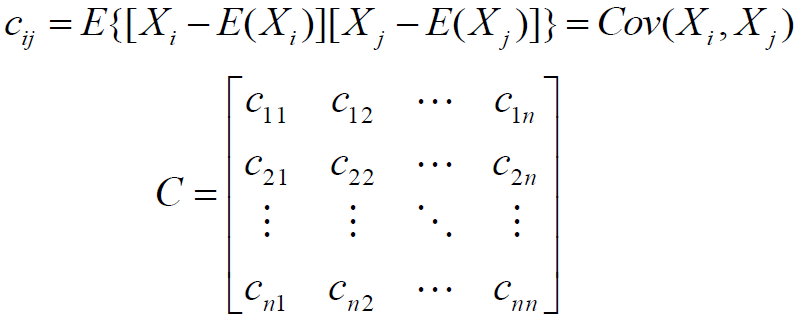
切比雪夫不等式

　　设随机变量 X 的期望为 μ，方差为 σ² ，对于任意正数 ε，有:

　　　　

　　证明：

　　　　

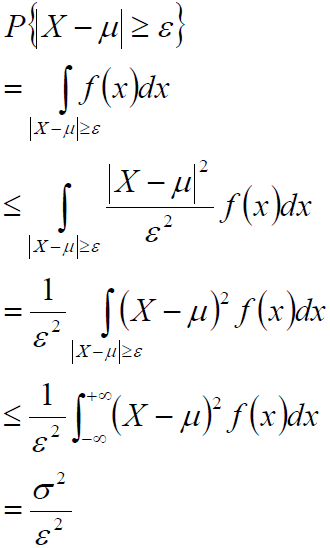
　　切比雪夫不等式说明， X 的方差越小， 事件{|X-μ| <ε} 发生的概率越大。即： X 取的值基本上集中在期望 μ 附近。

　　该不等式进一步说明了方差的含义。

　　该不等式可证明大数定理。

大数定律

　　设随机变量X₁,X₂…X_n…互相独立，并且具有相同的期望μ和方差σ²。作前n个随机变量的平均

　　　　

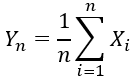
　　则对于任意正数ε，有

　　

　　大数定律的意义：

　　　　当 n 很大时，随机变量 X₁ ,X₂ …X_n 的平均值 Y_n在概率意义下无限接近期望 μ 。

　　　　　　出现偏离是可能的，但这种可能性很小，当 n 无限大时，这种可能性的概率为 0 。

　　重要推论：

　　　　一次试验中事件 A 发生的概率为 p ；重复 n 次独立试验中，事件 A 发生了 n_A 次，则 p 、 n 、n_A 的关系满足：对于任意正数ε

　　　　　　

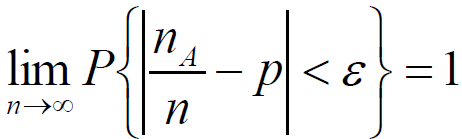
伯努利定理

　　上述推论是最早的大数定理的形式，称为伯努利定理。该定理表明事件 A 发生的频率n_A/n 以概率收敛于事件 A 的概率 p ，以严格的数学形式表达了频率的稳定性。

　　上述事实为我们在实际应用中用频率来估计概率提供了一个理论依据。　　　　

　　　　正态分布的参数估计
　　　　朴素贝叶斯做垃圾邮件分类
　　　　隐马尔可夫模型有监督参数学习

中心极限定理

　　设随机变量X₁,X₂…X_n…互相独立，服从同一分布，并且具有相同的期望μ和方差σ²，则随机变量

　　　　

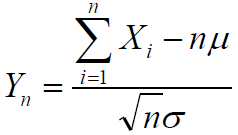
的分布收敛到标准正态分布。

　　容易得到： 收敛到正态分布N(nμ，nσ²)

例：标准的中心极限定理的问题

　　有一批样本 字符串 ))，其中 a-z 开头的比例是固定的，但是量很大，需要从中随机抽样。样本量 n ，总体但是量很大，需要从中随机抽样。样本量 n ，总体中 a 开头的字符串占比 1%，需要每次抽到的 a 开头的字符串占比 (0.99%,+ 1.01%)，样本量 n 至少是多少？

   问题可以重新表述一下：大量存在的两点分布B_i(1,p) p)，其中 B_i 发生的概率为 0.01 ，即 p=0.01 。取其中的 n 个，使得发生的个数除以总数的比例落在区间 ( 0.0099,0.0101)，则 n 至少是多少？

　　解：首先，两点分布B的期望为μ=p，方差为σ²=p(1-p)。

　　　　其次，当n较大时，随机变量近似服从正态分布，事实上

　　　　

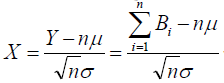
， 近似服从标准正态分布。

从而：

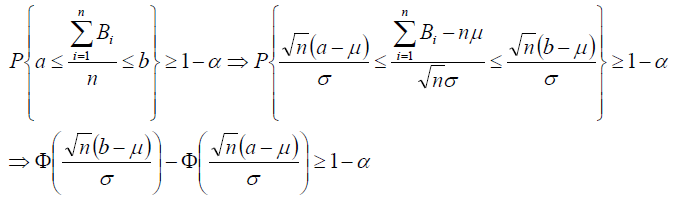
上式中， μ=0.01，σ2=0.0099，a=0.0099，b=0.0101，α=0.05或0.01(显著性水平的一般取值)，查标准正态分布表，很容易计算得到n的最小值。注：直接使用二项分布，也能得到结论。

中心极限定理的意义：

　　实际问题中，很多随机现象可以看做许多因素的 独立影响的综合反应 ，往往近似服从正态分布。

　　　　城市耗电量：大量用户的耗电量总和

　　　　测量误差：许多观察不到的、微小误差的总和

　　　　　　注意：是多个随机变量的和才可以，有些问题是乘性误差，则需要鉴别或者取对数后再使用。

　　　　线性回归 中，将使用该定理论证 最小二乘法的合理性

贝叶斯公式带来的思考

　　给定某些样本D，在这些样本中计算某结论A₁、A₂……A_n出现的概率，即P(A_i|D)

　　

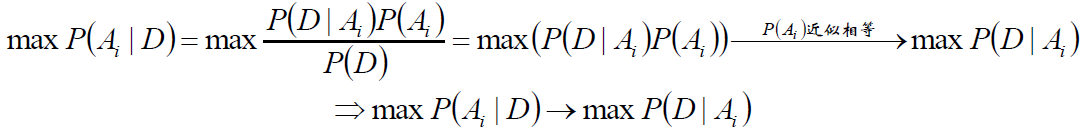
　　第一个等式：贝叶斯公式；

　　第二个等式：样本给定，则P(D)是常数；

　　第三个箭头：若这些结论A₁、A₂……A_n的先验概率相等(或近似)，则得到最后一个等式：即第二行的公式。

最大似然估计

　　设总体分布为 f(x,θ)， X₁ , X₂ … X_n 为该总体采样得到的样本。因为 X₁ , X₂ … X_n  独立同分布，于是，它们的联合密度函数为：

　　

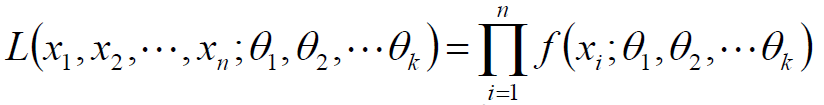
　　这里， θ 被看做固定但未知的参数；反过来，因为样本已经存在，可以看成 X₁ , X₂ … X_n 是固定的， L(x,θ)是关于 θ 的函数，即似然函数。

　　求参数 θ 的值，使得似然函数取最大值，这种方法就是最大似然估计。

最大似然估计的具体实践操作：

　　在实践中，由于求导数的需要，往往将似然函数取对数，得到对数似然函数；若对数似然函数可导，可通过求导的方式，解下列方程组，得到驻点，然后分析该驻点是极大值点：

　　

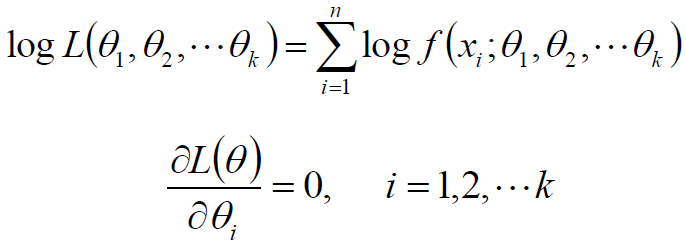
二项分布的最大似然估计：

　　投硬币试验中，进行N次独立试验，n次朝上，N-n次朝下。假定朝上的概率为p，使用对数似然函数作为目标函数：

　　

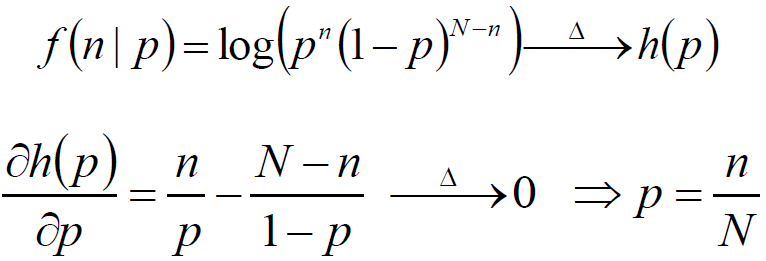
正态分布的最大似然估计：

　　若给定一组样本X₁ , X₂ … X_n ，已知它们来自于高斯分布 N(μ,σ)，试估计参数 μ,σ。

　　高斯分布的概率密度函数：

　　　　

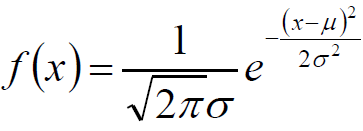
　　将X_i的样本值x_i带入，得到：

　　　　

　　

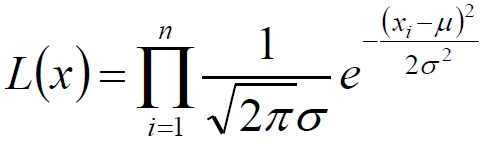
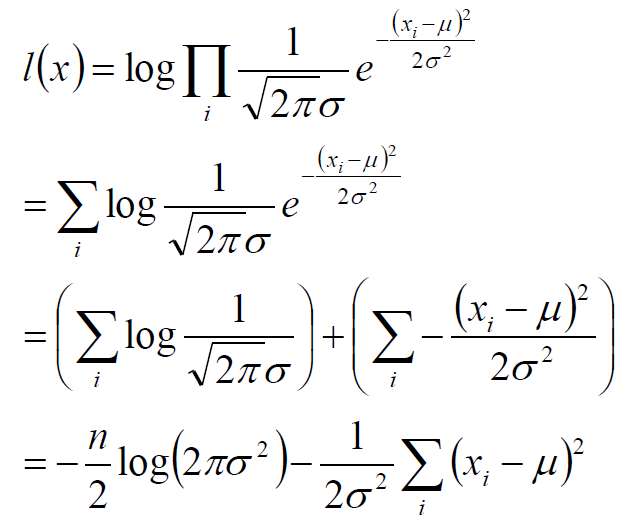
参数估计的结论：

　　目标函数：

　　　　

　　将目标函数对参数μ,σ分别求偏导，很容易得到μ,σ的式子：

　　　　

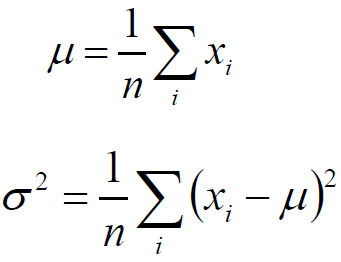
　　上述结论和矩估计的结果是一致的，并且意义非常直观：样本的均值即高斯分布的期望，样本的伪方差 即高斯分布的方差。

　　　　注：经典意义下的方差，分母是n-1 ；在似然估计的方法中，求的方差是 n

　　该结论将在期望最大化 EM 算法、高斯混合模型GMM 中将继续使用。