机器学习-贝叶斯网络-笔记

贝叶斯网络描述：

　　1）贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directedacyclic graphical model)，是一种概率图模型，是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。考察一组随机变量{X₁,X₂...X_n}及其n组条件概率分布(Conditional Probability Distributions, CPD)的性质。

　　2）一般而言，贝叶斯网络的有向无环图中的节点表示随机变量，它们可以是可观察到的变量，或隐变量、未知参数等。连接两个节点的箭头代表此两个随机变量是具有因果关系(或非条件独立)。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。

　　3）每个结点在给定其直接前驱时，条件独立于其非后继。

一个简单的贝叶斯网络：

　　p(a,b,c) = p(c|a,b)p(b|a)p(a)

　　对应的有向无环图：

　　

全连接贝叶斯网络：

　　每一对结点之间都有边连接

　　p(x₁,...,x_k)=p(x_k|x₁,...,x_k-1)...p(x₂|x₁)p(x₁)

　　

一个“正常”的贝叶斯网络:

　　

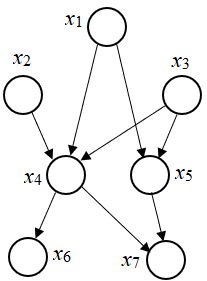
　　1)有些边缺失

　　2)直观上：x₁和x₂独立,x₆和x₇在x₄给定的条件下独立

　　3)x₁,x₂,…x₇的联合分布：

　　p(x₁)p(x₂)p(x₃)p(x₄|x₁,x₂,x₃)p(x₅|x₁,x₃)p(x₆|x₄)p(x₇|x₄,x₅)

贝叶斯网络的3种结构形式：

　　先引入D-分离(D-Separation)的概念：是一种用来判断变量是否条件独立的图形化方法。即对于一个DAG(有向无环图)E，D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。

形式1：head-to-head

　　贝叶斯网络的第一种结构形式：

　　

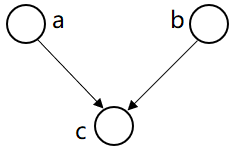
　　P(a,b,c) =P(a)*P(b)*P(c| a,b)

　　

　　→P(a,b)=P(a)*P(b)

　　在c未知的条件下，a，b被阻断(blocked)是独立的

形式2：tail-to-tail

　　

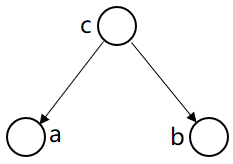
　　根据图模型，得：P(a,b,c)=P(c)*P(a|c)*P(b|c)
       从而： P(a,b,c)/P(c)= P(a|c)*P(b|c)
   　因为 P(a,b|c)=P(a,b,c)/P(c)
       得：P(a,b|c)=P(a|c)*P(b|c)
       即：在c给定的条件下，
      a，b被阻断(blocked)是独立的

形式3：head-to-tail

　　

　　P(a,b,c)=P(a)*P(c|a)*P(b|c)

　　即：在c给定的条件下，a，b被阻断(blocked)，是独立的。

 

朴素贝叶斯:

1) 朴素贝叶斯的假设

　　一个特征出现的概率，与其他特征(条件)独立(特征独立性),其实是：对于给定分类的条件下，特征独立

　　每个特征同等重要(特征均衡性)

2) 朴素贝叶斯的推导

　　朴素贝叶斯(Naive Bayes，NB)是基于“特征之间是独立的”这一朴素假设，应用贝叶斯定理的监督学习算法。

　　对于给定的特征向量x₁,x₂,...,x_n

　　类别y的概率可以根据贝叶斯公式得到：

　　

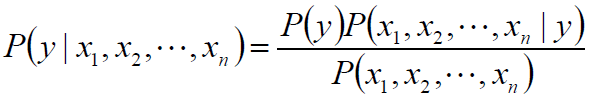
　　使用朴素的独立性假设：

　　P(x_i|y,x₁,...,x_i-1,x_i+1,...,x_n)=P(x_i|y)

　　类别y的概率可简化为：

　　　

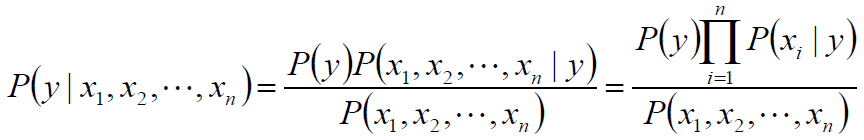
　　在给定样本的前提下，P(x₁,x₂,...,x_n) 是常数：

　　

　　从而：

　　

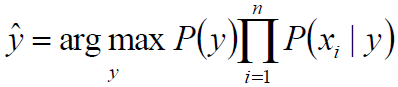
高斯朴素贝叶斯Gaussian Naive Bayes：

　　根据样本使用MAP(Maximum A Posteriori 极大后验估计)估计 P(y)，建立合理的模型估计P(x_i|y) ，从而得到样本的类别。
　　
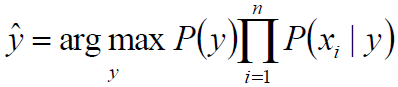
　　假设特征服从高斯分布，即：

　　

　　参数使用MLE(极大似然估计)估计即可。

多项分布朴素贝叶斯Multinomial Naive Bayes：

　　假设特征服从多项分布，从而，对于每个类别y，参数为θ_y=(θ_y1,θ_y2,...,θ_yn),其中n为特征的数目,P(x_i|y)的概率为θ_yi。

　　参数 使用MLE估计的结果为：　

　　　

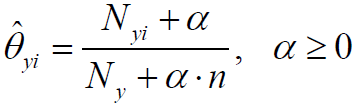
　　假定训练集为T，有：

　　　　

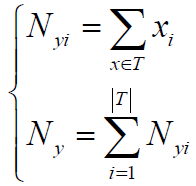
　　其中，α=1称为Laplace平滑，α<1称为Lidstone平滑。

拉普拉斯Laplace平滑　　

　　p(x₁|c₁)是指的:在垃圾邮件c₁这个类别中，单词x₁出现的概率。
      x₁是待考察的邮件中的某个单词定义符号
      n₁：在所有垃圾邮件中单词x1出现的次数。如果x1没有出现过，则n₁=0。
      n：属于c₁类的所有文档的出现过的单词总数目。

　　得到公式：p(x₁|c₁)=n₁/n

　　拉普拉斯平滑：p(x₁|c₁)=(n₁+1)/(n+N),其中，N是所有单词的数目。修正分母是为了保证概率和为1

　　同理，以同样的平滑方案处理p(x₁)

对朴素贝叶斯的思考

　　拉普拉斯平滑能够避免0/0带来的算法异常
     要比较的是P(c₁|x)和P(c₂|x) 的相对大小，而根据公式P(c|x) =P(x|c)*P(c) / P(x)，二者的分母都是除以P(x)，实践时可以不计算该系数。
     问题：一个词在样本中出现多次，和一个词在样本中出现一次，形成的词向量相同
    　　 由0/1向量改成频数向量或TF-IDF向量
     如何判断两个文档的距离
     　　夹角余弦

　  如何给定合适的超参数: 

　　

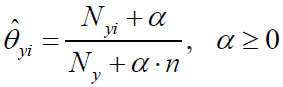
　　　　交叉验证