机器学习-聚类-密度聚类算法笔记
密度聚类方法:1.DBSCAN 2.密度最大值算法
密度聚类方法的指导思想是,只要样本点的密度大于某阈值,则将该样本添加到最近的簇中。
这类算法能克服基于距离的算法只能发现“类圆形”(凸)的聚类的缺点,可发现任意形状的聚类,且对噪声数据不敏感。但计算密度单元的计算复杂度大,需要建立空间索引来降低计算量。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同,它将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在有“噪声”的数据中发现任意形状的聚类。
对象的ε-邻域:给定对象在半径ε内的区域。
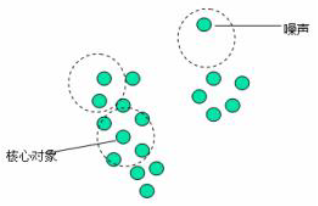
核心对象:对于给定的数目m,如果一个对象的ε-邻域至少包含m个对象,则称该对象为核心对象。
直接密度可达:给定一个对象集合D,如果p是在q的ε-邻域内,而q是一个核心对象,我们说对象p从对象q出发是直接密度可达的。
如图ε=1cm,m=5,q是一个核心对象,从对象q出发到对象p是直接密度可达的。
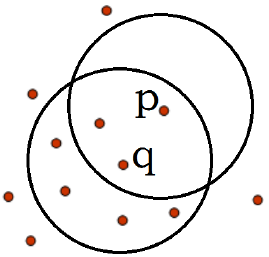
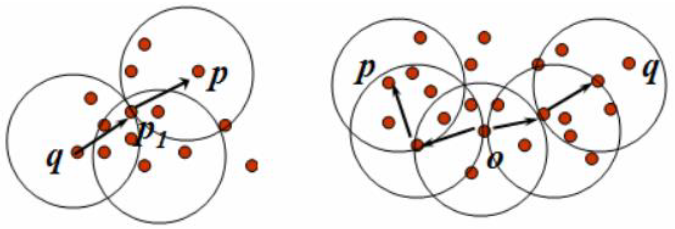
密度可达:如果存在一个对象链p1p2…pn,p1=q,pn=p,对pi∈D,(1≤i ≤n),pi+1是从pi关于ε和m直接密度可达的,则对象pi+1是从对象q关于ε和m密度可达的。
密度相连:如果对象集合D中存在一个对象o,使得对象p和q是从o关于ε和m密度可达的,那么对象p和q是关于ε和m密度相连的。
簇:一个基于密度的簇是最大的密度相连对象的集合。
噪声:不包含在任何簇中的对象称为噪声
DBSCAN算法流程:
如果一个点p的ε-邻域包含多于m个对象,则创建一个p作为核心对象的新簇;
寻找并合并核心对象直接密度可达的对象;
没有新点可以更新簇时,算法结束。
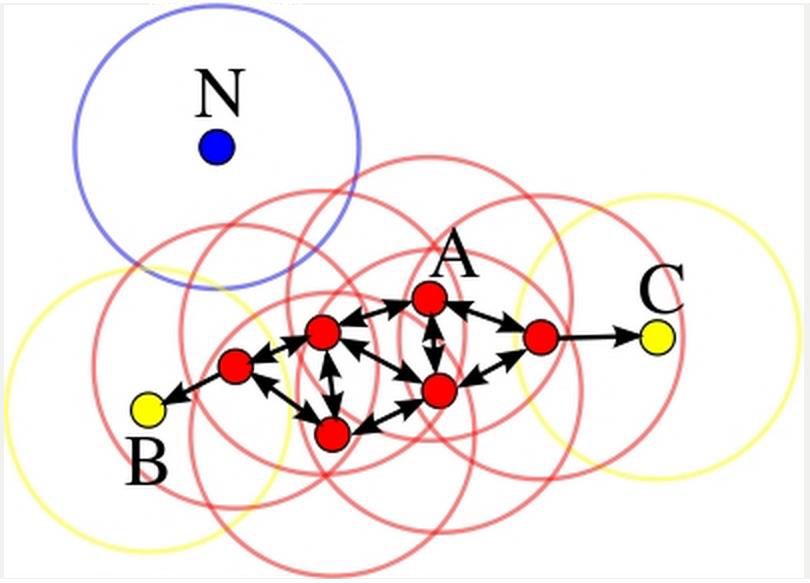
由上述算法可知:
每个簇至少包含一个核心对象;
非核心对象可以是簇的一部分,构成了簇的边缘(edge);
包含过少对象的簇被认为是噪声
密度最大值聚类
密度最大值聚类是一种简洁优美的聚类算法, 可以识别各种形状的类簇, 并且参数很容易确定。
定义:局部密度ρi,截断值:

dc是一个截断距离, ρi即到对象i的距离小于dc的对象的个数。由于该算法只对ρi的相对值敏感, 所以对dc的选择是稳健的,一种推荐做法是选择dc,使得平均每个点的邻居数为所有点的1%-2%
高斯核相似度:
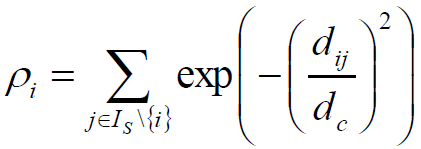
K近邻均值:
![]()
定义:高局部密度点距离δi
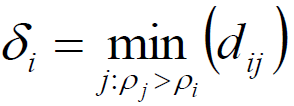
在密度高于对象i的所有对象中,到对象i最近的距离,即高局部密度点距离。
1.对于密度最大的对象,设臵δi=max(dij)(即:该问题中的无穷大)。
2.只有那些密度是局部或者全局最大的点才会有远大于正常值的高局部密度点距离。
簇中心的识别
1)那些有着比较大的局部密度ρi和很大的高密距离δi的点被认为是簇的中心;
2)高密距离δi较大但局部密度ρi较小的点是异常点;
确定簇中心之后,其他点按照距离已知簇的中心最近进行分类
注:也可按照密度可达的方法进行分类。
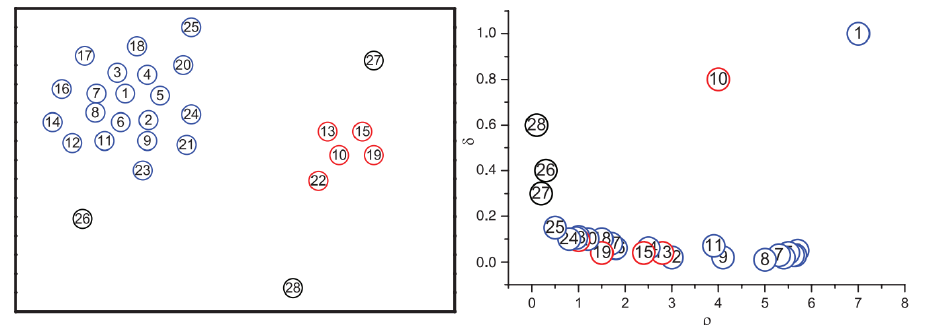
DensityPeak与决策图Decision Graph
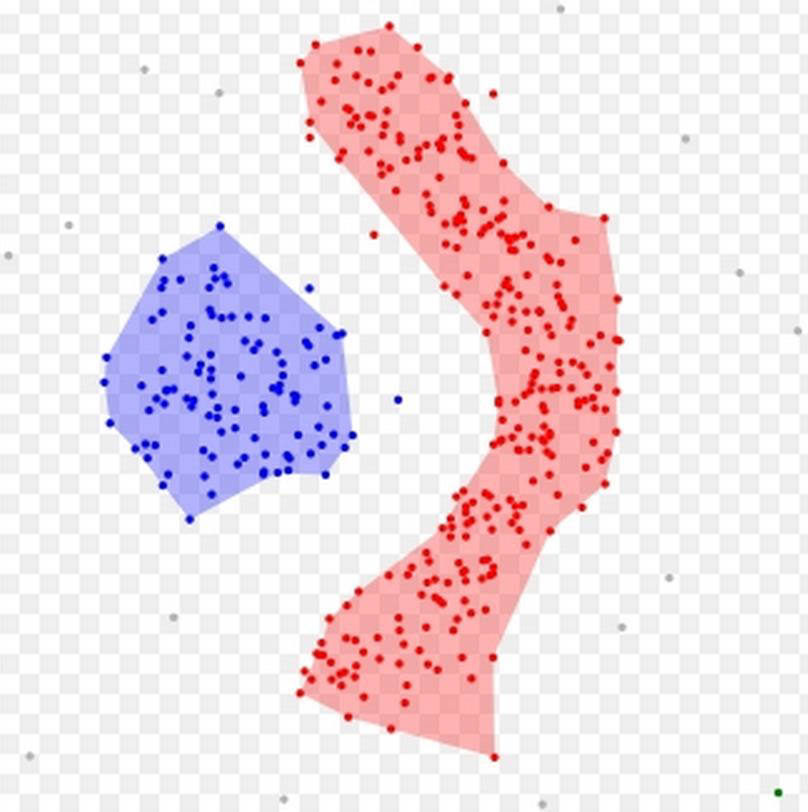
左图是所有点在二维空间的分布, 右图是以ρ为横坐标, 以δ为纵坐标绘制的决策图。可以看到,1和10两个点的ρi和δi都比较大,作为簇的中心点。26、27、28三个点的δi也比较大,但是ρi较小,所以是异常点。
边界和噪声的重认识
1)在聚类分析中,通常需要确定每个点划分给某个簇的可靠性:
2)在该算法中,可以首先为每个簇定义一个边界区域(border region),亦即划分给该簇但是距离其他簇的点的距离小于dc的点的集合。然后为每个簇找到其边界区域的局部密度最大的点,令其局部密度为ρh。
3)该簇中所有局部密度大于ρh的点被认为是簇核心的一部分(亦即将该点划分给该类簇的可靠性很大),其余的点被认为是该类簇的光晕(halo),亦即可以认为是噪声。
注:关于可靠性问题,在EM算法中仍然会有相关涉及。
Affinity Propagation: AP聚类算法,可以看看此文。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号