机器学习-聚类-k-Means算法笔记
聚类的定义:
聚类就是对大量未知标注的数据集,按数据的内在相似性将数据集划分为多个类别,使类别内的数据相似度较大而类别间的数据相似度较小,它是无监督学习。
聚类的基本思想:
给定一个有N个对象的数据集,构造数据的k个簇,k≤n。满足下列条件:
1. 每一个簇至少包含一个对象
2. 每一个对象属于且仅属于一个簇
3. 将满足上述条件的k个簇称作一个合理划分
基本思想:对于给定的类别数目k,首先给出初始划分,通过迭代改变样本和簇的隶属关系,使得每一次改进之后的划分方案都较前一次好。
k-Means算法:
k-Means算法,也被称为k-平均或k-均值,是一种广泛使用的聚类算法,或者成为其他聚类算法的基础。
假定输入样本为S=x1,x2,...,xm,则算法步骤为:
1. 选择初始的k个类别中心μ1μ2…μk
2. 对于每个样本xi,将其标记为距离类别中心最近的类别,即:
![]()
3. 将每个类别中心更新为隶属该类别的所有样本的均值
![]()
4. 重复最后两步,直到类别中心的变化小于某阈值。
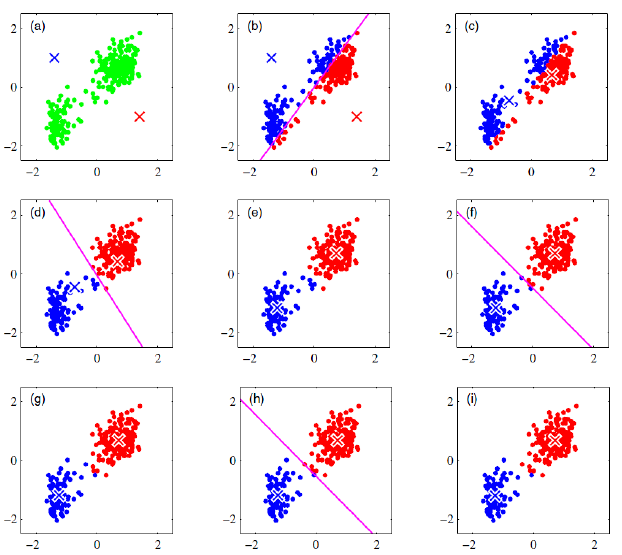
K-means的图解过程可以看一下这个作者所写的样例。
距离计算方法总结
不同距离的度量其聚类结果不同,以下是距离度量的一些方法:
(1)闵可夫斯基距离Minkowski/欧式距离
![]()
(2)杰卡德相似系数(Jaccard)
![]()
(3)余弦相似度(cosine similarity)
![]()
(4)Pearson相似系数
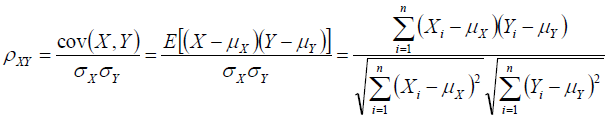
(5)相对熵(K-L距离)
![]()
(6)Hellinger距离(该距离满足三角不等式,是对称、非负距离)
![]()
余弦相似度与Pearson相似系数
n维向量x和y的夹角记做θ,根据余弦定理,其余弦值为:
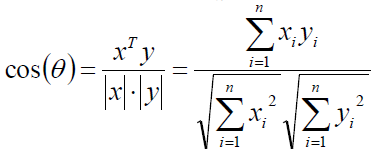
这两个向量的相关系数是:
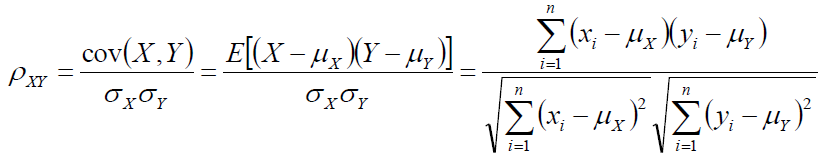
相关系数即将x、y坐标向量各自平移到原点后的夹角余弦!
这即解释了为何文档间求距离使用夹角余弦——因为这一物理量表征了文档去均值化后的随机向量间相关系数。
K-means具有如下优点:
(1)当簇近似为高斯分布时,它的效果较好。
(2)收敛速度快,往往只需要5~6步即可达到收敛。
(3)算法复杂度为O(tkn)。n为数据项个数,k为要聚类成的簇数,t为迭代次数。而通常,k<<n,所以,对于大数据集,k-means算法相对可伸缩,且有效。
K-means也有一些缺点:
(1)需要注意的是初始簇心的选择有时候会影响最终的聚类结果,由于聚类算法为无监督学习,人们事先无法确定到底需要分多少个簇,也就是说k值无法提前确定。所以,实际操作中,我们一般会选用不同的数据作为初始簇心,多次执行k-means算法,为了解决这个问题,k-means++算法应运而生。
(2)对噪声和孤立点影响敏感。我们可以看出K-means中means表示平均值,而平均值往往对噪声敏感,一个离群点往往会对整个结果造成很大影响。
(3)不适合于发现非凸形状的簇或者大小差别很大的簇。
(4)在簇的平均值可被定义的情况下才能使用,可能不适用于某些应用
对k-Means的思考:
k-Means将簇中所有点的均值作为新质心,若簇中含有异常点,将导致均值偏离严重。以一维数据为例:
1. 数组1、2、3、4、100的均值为22,显然距离“大多数”数据1、2、3、4比较远
2. 改成求数组的中位数3,在该实例中更为稳妥。
3. 这种聚类方式即k-Mediods聚类(K中值距离)
二分k-Means算法(Bisecting k-Means):
由于传统的KMeans算法的聚类结果易受到初始聚类中心点选择的影响,因此在传统的KMeans算法的基础上进行算法改进,对初始中心点选取比较严格,各中心点的距离较远,这就避免了初始聚类中心会选到一个类上,一定程度上克服了算法陷入局部最优状态。
二分KMeans(Bisecting
KMeans)算法的主要思想是:首先将所有点作为一个簇,然后将该簇一分为二。之后选择能最大限度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇。以此进行下去,直到簇的数目等于用户给定的数目k为止。以上隐含的一个原则就是:因为聚类的误差平方和能够衡量聚类性能,该值越小表示数据点越接近于他们的质心,聚类效果就越好。所以我们就需要对误差平方和最大的簇进行再一次划分,因为误差平方和越大,表示该簇聚类效果越不好,越有可能是多个簇被当成了一个簇,所以我们首先需要对这个簇进行划分。
k-means++算法:
k-means++是k-means的变形,通过小心选择初始簇心,来获得较快的收敛速度以及聚类结果的质量。
先随机选择一个数据项作为第一个初始的簇心(当然,最终我们要选择k个),根据这1个簇心,我们通过一系列计算,获得第2个簇心,再根据这2个簇心,通过计算获得第3个簇心。。。以此类推,最终,获得全部的k个簇心,然后,再按照上面k-means的做法,做聚类分析。
那么究竟怎样的选择就是合理的选择簇心呢?在此我们有这样一个原则:假设现在已经选择了r个簇心,要接着选取第r+1个簇心。那么当然是应该选择距离其簇心较远的数据点当新的簇心。可以脑补这样一个场景:r个簇心,每个数据点都对应着且只对应着一个簇心,这个簇心当然是相对于其他r−1个簇心来说,是距离这个数据点最近的。于是每个点,都与其簇心有条连线,连线的长度就是这个数据点到簇心的距离,我们现在要做的,就是选择距离其簇心距离较大的那个数据点。为什么是“较大”,而不是“最大”,数据中可能会存在最大距离噪声,而且第一次选择簇心是随机的,所以每次不一定都要精确,经过多次迭代反而会跑偏,当然k-means++即使比传统的k-means更好,却依然是一种启发式的算法,不能说这种做法最终的结果就一定是最优的。
如何选择离簇心距离“较大”的数据点呢?假设,现在将所有的数据点与其对应簇心连接,那么会构成n条连线(n是数据项的个数,自己与自己连接的情况,可以看做是构成了一条长度为0的线),我们记这n条连线的长度为Dis1,Dis2,…Disn,然后把这n条连线按随机的顺序,首尾相连,构成一条长度为∑Disi的连线,然后现在随机抛出一点,落在这条“总线”上,那么显然,落在距离较长的线上的概率更高一些。
选择下一簇心的具体方法操作如下:
(1)对已经选出作为簇心的r个点(r<k),计算数据集中每个数据项应该归类的簇,以及距离
(2)将这n个距离求和,得到sum(Dis_i),然后随机选取一个小于sum(Dis_i)的值Random
(3)令Random依次减去Disi,Random -= Disi,直到Random <= 0为止,此时,Random减去的Disi所对应的数据项就是新的簇心。
综上,k-means++算法步骤如下:
(1)随机选择一个数据项,作为第一个簇心
(2)根据选择下一个簇心的操作方法(上面列出的3步),选择下一簇心
(3)重复步骤2,直到得到全部的k个簇心
K-Means||算法:
解决K-Means++算法缺点而产生的一种算法;主要思路是改变每次遍历时候的取样规则,并非按照K-Means++算法每次遍历只获取一个样本,而是每次获取K个样本,重复该取样操作O(logn)次__(n是样本的个数)__,然后再将这些抽样出来的样本聚类出K个点,最后使用这K个点作为K-Means算法的初始聚簇中心点。实践证明:一般5次重复采用就可以保证一个比较好的聚簇中心点。
算法步骤:
(1)在N个样本中抽K个样本,一共抽logn次,形成一个新的样本集,一共有Klogn个数据。
(2)在新数据集中使用K-Means算法,找到K个聚簇中心。
(3)把这K个聚簇中心放到最初的样本集中,作为初始聚簇中心。
(4)原数据集根据上述初始聚簇中心,再用K-Means算法计算出最终的聚簇。
其它的K-means衍生算法--Canopy算法、Mini Batch K-Means,可以看一下其它的介绍
聚类的衡量指标1
(1)均一性:一个簇只包含一个类别的样本,则满足均一性可以认为是分类算法衡量的精确率(每个聚类簇中正确分类的样本数占该聚类簇中的样本数),如果一个簇中的类别只有一个,则均一性为1;如果有多个类别,计算该类别下的簇的条件经验熵H(C|K),值越大则均一性越小。
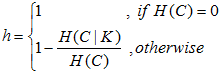
(2)完整性:同类别的样本被归类到同一聚类簇中,则满足完整性。可以认为是分类算法衡量的召回率(每个聚类中正确分类的样本数占该类别样本的数量),如果同类样本全部被分在同一个簇中,则完整性为1;如果同类样本被分到不同簇中,计算条件经验熵H(K|C),值越大则完整性越小。
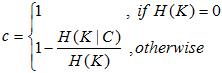
(3)V_measure:均一性和完整性加权平均,如果β>1则更注重完整性,如果β<1则更注重均一性。
![]()
聚类的衡量指标2
1)兰德指数RI
Rand Index计算样本预测值与真实值之间的相似度,RI取值范围是[0,1],值越大意味着聚类结果与真实情况越吻合。![]()
其中C表示实际类别信息,K表示聚类结果,a表示在C与K中都是同类别的元素对数,b表示在C与K中都是不同类别的元素对数,由于每个样本对仅能出现在一个集合中,因此有TP+FP+TN+FN=C2m=m(m-1)/2表示数据集中可以组成的样本对数。
对于随机结果,RI并不能保证分数接近0,因此具有更高区分度的Adjusted Rand Index被提出,取值范围是[-1,1],值越大表示聚类结果和真实情况越吻合。
2)调整兰德指数ARI:
数据集S共有N个元素,两个聚类结果分别是:
X={X1,X2,...,Xr} Y={Y1,Y2,...,Ys}

X和Y的元素个数为:a={a1,a2,...,ar} b={b1,b2,...,bs}
记:nij=|Xi∩Yi|
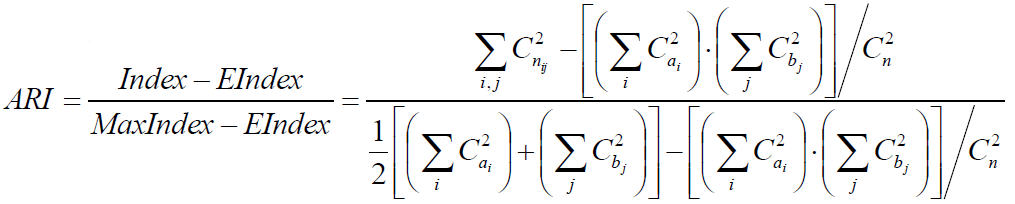
聚类的衡量指标3
使用与ARI相同的记号,根据信息熵,得:
互信息/正则化互信息:
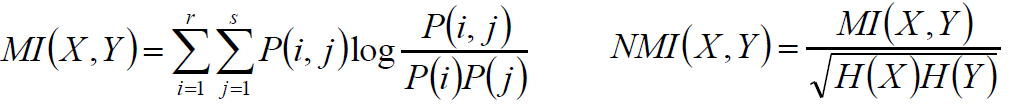
X服从超几何分布,求互信息期望:
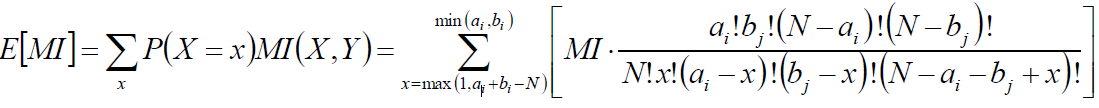
借鉴ARI,有:

聚类的衡量指标4
轮廓系数(Silhouette):
1)Silhouette系数是对聚类结果有效性的解释和验证,由Peter J. Rousseeuw于1986提出。
2)计算样本i到同簇其他样本的平均距离ai。ai越小,说明样本i越应该被聚类到该簇。将ai称为样本i的簇内不相似度。簇C中所有样本的ai均值称为簇C的簇不相似度。
3)计算样本i到其他某簇Cj的所有样本的平均距离bij,称为样本i与簇Cj的不相似度。定义为样本i的簇间不相似度:bi=min{bi1,bi2,……bik},bi越大,说明样本i越不属于其他簇。
4)根据样本i的簇内不相似度ai和簇间不相似度bi,定义样本i的轮廓系数:
![]()
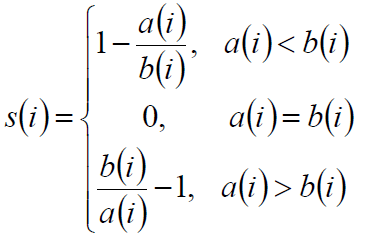
si接近1,则说明样本i聚类合理;si接近-1,则说明样本i更应该分类到另外的簇;若si近似为0,则说明样本i在两个簇的边界上。
所有样本的si的均值称为聚类结果的轮廓系数,是该聚类是否合理、有效的度量。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号