机器学习之决策树笔记
决策树
1.决策树是一种树型结构,其中每个内部结点表示在一个属性上的测试,每个分支代表一个测试输出,每个叶子结点代表一种类别。
2.决策树学习是以实例为基础的归纳学习
3.决策树学习采用的是自顶向下的递归方法,其基本思想是以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵值为零,此时每个叶子节点中的实例都属于同一类。
决策树学习算法的特点
1.决策树学习算法的最大优点是,它可以自学习。在学习的过程中,不需要使用者了解过多背景知识,只需要对训练实例进行较好的标注,就能够进行学习
2.显然,它属于有监督学习
3.从一类无序、无规则的事物中推理出决策树表示的分类规则
4. 非参数学习算法,可以解决多分类问题,也可以解决回归问题,非常好的可解释性
建立决策树的关键,即在当前状态下选择哪个属性作为分类依据。根据不同的目标函数,建立决策树主要有以下三种算法
1.ID3:使用信息增益/互信息g(D,A)进行特征选择
2.C4.5:信息增益率
3.CART:基尼指数
建立决策树需要知道信息熵
熵在信息论中代表随机变量不确定度的度量
1)熵越大,数据的不确定性越高
2)熵越小,数据的不确定性越低
![]()
pi为第i个事件发生的概率
接着是条件熵
H(X,Y)-H(X)
(X,Y)发生所包含的熵,减去X单独发生包含的熵:在X发生的前提下,Y发生“新”带来的熵。
该式子定义为X发生前提下,Y的熵:
条件熵H(Y|X)
推导条件熵的定义式

根据条件熵的定义式,可以得到
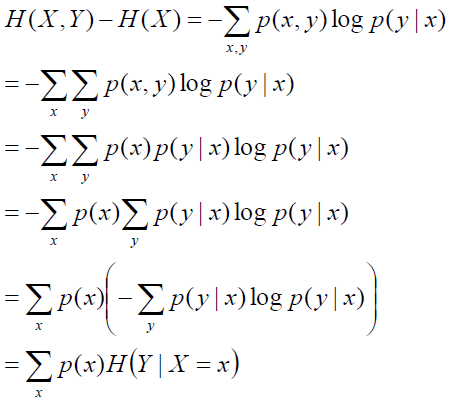
建立决策树分类依据之信息增益
概念:当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时,所对应的熵和条件熵分别称为经验熵和经验条件熵
信息增益表示得知特征A的信息而使得类X的信息的不确定性减少的程度
定义:特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A
给定条件下D的经验条件熵H(D|A)之差,即:
g(D,A)=H(D)-H(D|A),显然,这即为训练数据集D和特征A的互信息。
信息增益的计算方法
设训练数据集为D,|D|表示样本个数。
设有K个类Ck,k=1,2,…K, |Ck|为属于类Ck的样本个数,有:Σk|Ck|=|D|
设特征A有n个不同的取值{a1, a2,…an,},根据特征A的取值将D划分为n个子集D1, D2,…Dn ,|Di|为Di的样本个数,有:Σi|Di|=|D|
记子集Di中属于Ck的样本的集合为Dik, |Dik|为Dik的样本个数
计算数据集D的经验熵
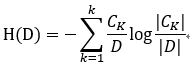
遍历所有特征,对于特征A:
计算特征A对数据集D的经验条件熵H(D|A)
计算特征A的信息增益:g(D,A)=H(D)-H(D|A)
选择信息增益最大的特征作为当前的分裂特征
经验条件熵H(D|A)
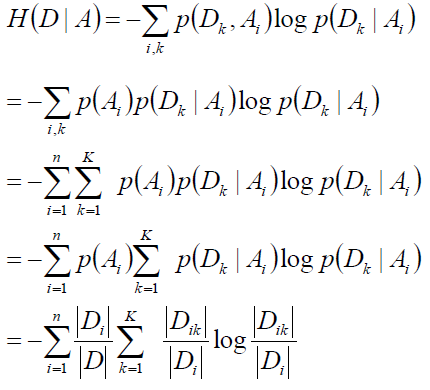
实际上,信息增益准则对可取值数目较多的属性有所偏好,例,如果把所有样本进行有序的编号1,2,3,...,n,如果将编号进行属性划分,那么编号结点将产生n个分支,每个分支结点仅包含一个样本,这些分支结点的纯度已达最大,然而这样的决策树显然不具有泛化能力,无法对新样本进行预测。为减少这种偏好可能带来的不利影响,C4.5决策树算法不直接使用信息增益,而是用“增益率”来选择最优划分属性,
信息增益率:gr(D,A)=g(D,A)/H(A)
需要注意的是,增益率准则对可取值数目较少的属性有所偏好,因此,C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
CART决策树使用“基尼指数”来选择划分属性

基尼指数反应的是从数据集D中随机抽取两个样本,其类别标记不一致的概率。因此基尼指数越小则数据集D的纯度越高。于是在候选属性集合A中,选择那个使得划分后基尼指数最小的属性作为最优划分属性。
当然以上如果有读者还是不太清楚,可以看看具体的示例https://blog.csdn.net/wsp_1138886114/article/details/80955528
决策树的过拟合
决策树对训练数据有很好的分类能力,但对未知的测试数据未必有好的分类能力,泛化能力弱,即可能发生过拟合现象
剪枝:
三种决策树的剪枝过程算法相同,区别仅是对于当前树的评价标准不同。
信息增益、信息增益率、基尼系数
剪枝总体思路:
由完全树T0开始,剪枝部分结点得到T1,再次剪枝部分结点得到T2…直到仅剩树根的树Tk;
在验证数据集上对这个树分别评价,选择损失函数最小的树Tα
根据原损失函数

叶节点越多,决策树越复杂,损失越大,修正:
![]()
当α=0时,未剪枝的决策树损失最小
当α=+∞时,单根结点的决策树损失最小
假定当前对以r为根的子树剪枝:
剪枝后,只保留r本身而删掉所有的叶子
考察以r为根的子树:
剪枝后的损失函数:![]()
剪枝前的损失函数:![]()
令二者相等,求得:
![]()
α称为结点r的剪枝系数
对于给定的决策树T0:
计算所有内部结点的剪枝系数;
查找最小剪枝系数的结点,剪枝得到决策树Tk;
重复以上步骤,直到决策树Tk只有1个节点;
得到决策树序列T0, T1, T2,…TK;
使用验证样本集选择最优子树
使用验证集做最优子树的标准,可以使用评价函数:
![]()





