机器学习之softmax回归笔记
本次笔记绝大部分转自https://www.cnblogs.com/Luv-GEM/p/10674719.html
softmax回归
Logistic回归是用来解决二类分类问题的，如果要解决的问题是多分类问题呢？那就要用到softmax回归了，它是Logistic回归在多分类问题上的推广。此处神经网络模型开始乱入，softmax回归一般用于神经网络的输出层，此时输出层叫做softmax层。
1、softmax函数
首先介绍一下softmax函数，这个函数可以将一个向量(x1,x2,...,xK)映射为一个概率分布(z1,z2,...,zK)，它将数据的范围映射到（0,1）区间：
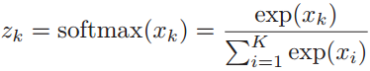
那么在多分类问题中，假设类别标签y∈{1, 2, ..., C}有C个取值，那么给定一个样本x，softmax回归预测x属于类别c的后验概率为：
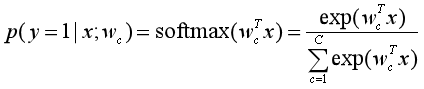
其中wc是第c类的权重向量。
那么样本x属于C个类别中每一个类别的概率用向量形式就可以写为：
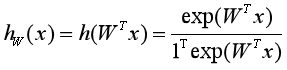
其中W=[w1,w2,...,wC]是由C个类的权重向量组成的矩阵，1表示元素全为1的向量，得到
是由所有类别的后验概率组成的向量，第c个元素就是预测为第c类的概率，比如[0.05, 0.01, 0.9, 0.02, 0.02]，预测为第3类。
2、softmax回归的损失函数和梯度下降
one-hot向量：[0,0,0,1,0,...,0,0]这个向量就表示第四个类别标签，1所在的位置就是那个位置的类标签，其它全设置为0。
假设训练数据集为{(x1,y1),(x2,y2),...(xM, yM)}，即有M个样本，softmax回归使用交叉熵损失函数来学习最优的参数矩阵W，对样本进行分类。
由于涉及到多分类，所以损失函数的表示方法稍微复杂一些。我们用C维的one-hot向量y来表示类别标签。对于类别c，其向量表示为：
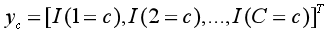
其中
表示指示函数。
则softmax回归的交叉熵损失函数为：
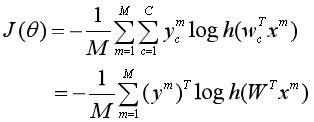
其中
表示样本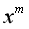
预测为每个类别的后验概率组成的向量。
上面这个式子不太好理解，我们单独拿出一个样本来观察。假设类别有三类，预测一个样本x属于第2类的交叉熵损失为
，其中
，如果预测正确，如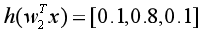
，则交叉熵损失为
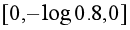，而如果预测错误，如
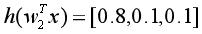，则交叉熵损失为
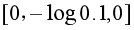，可见预测错误时损失非常大。
同样的，用梯度下降法对损失函数进行优化求解，首先得到损失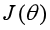
对参数向量W的梯度：
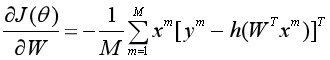
初始化W0=0，然后对所有参数WC进行迭代更新，直至收敛。
参考资料：
1、吴恩达：《机器学习》
2、邱锡鹏：《神经网络与深度学习》
3、 https://blog.csdn.net/u010867294/article/details/79138603
