栈和队列
0.PTA得分截图

1.本周学习总结
1.1.1 栈的介绍
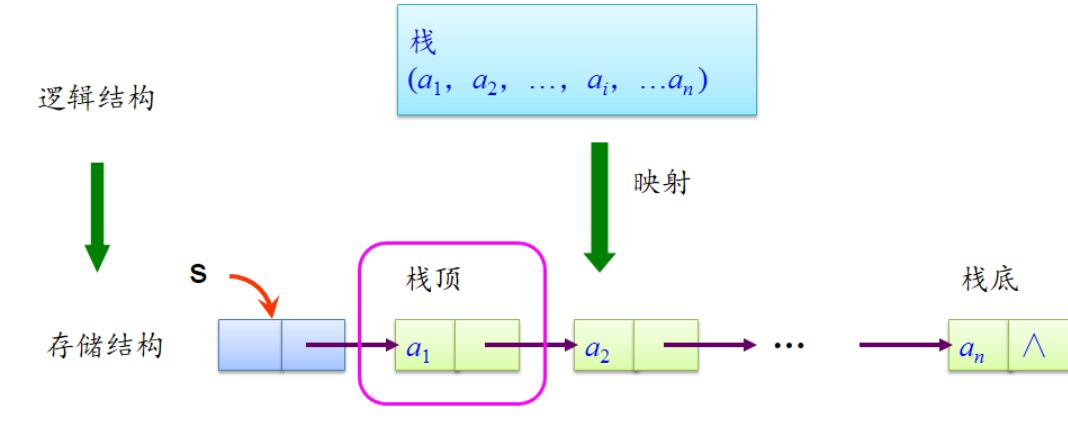
栈作为一种数据结构,是一种只能在一端进行插入和删除操作的特殊线性表。它按照后进先出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据,最后一个数据被第一个读出来。栈具有记忆作用,对栈的插入与删除操作中,不需要改变栈底指针。
栈是允许在同一端进行插入和删除操作的特殊线性表。允许进行插入和删除操作的一端称为栈顶,另一端为栈底;栈底固定,而栈顶浮动;栈中元素个数为零时称为空栈。插入一般称为进栈,删除则称为退栈。
- 栈中元素的特性
. 具有线性关系
. 后进先出 - 栈的进栈出栈原则
. 栈顶出栈->栈底最后出栈
. 时进时出->元素未完全进栈时,即可出栈 - 两种存储结构:顺序存储结构和链式存储结构
![]()
1.1.2 顺序栈
顺序栈介绍
利用一组地址连续的存储单元依次存放栈底到栈顶的数据元素,栈底位置固定不变,栈顶位置随着入栈和出栈操作而变化。

顺序栈四要素:
- 栈空条件:top = -1
- 栈满条件:top = MaxSize - 1
- 进栈e操作:top++;st->data[top] = e
- 退栈操作:e = st->data[top];top--
定义结构体
假设栈的元素个数最大不超过正整数MaxSize,所有元素都具有同一元素数据类型ElemType,则栈类型SqStack定义为
typedef struct
{
ElemType data[MaxSize];
int top;//栈顶指针
}Stack;
typedef Stack* SqStack;
初始化栈
void InitStack(SeqStack *S)
{
/* top为-1表示空栈 */
S->top = -1;
}
栈顶元素下标 top 等于 -1 为空栈,所以只需将 top 赋值 -1 即可完成顺序栈的初始化。
销毁栈
void DestroyStack(SqStack &s)
{
delete s;
}
判断栈是否为空
bool StackEmpty(SqStack s)
{
return(s->top==-1)
}
进栈
在栈不满的条件下,先将栈指针增1,然后在该位置上插入元素e。
bool Push(SqStack &s, ElemType e)
{
if (s->top == MaxSize - 1)
return false;
s->top++;
s->data[s->top] = e;
return true;
}
出栈
在栈不为空的条件下,先将栈顶元素赋给e,然后将栈指针减1.
bool Pop(SqStack &s, ElemType &e)
{
if (s->top == -1)//栈为空的情况下,栈下溢出
return false;
e = s->data[s->top];//取栈顶指针元素
s->top--;
return true;
}
取栈顶元素
在栈不为空的条件下,将栈顶元素赋给e。
bool GetTop(SqStack *s, ElemType &e)
{
if (s->top == -1)//栈为空的情况
return false;
e = s->data[s->top];
return true;
}
1.1.3 共享栈
如果需要用到两个相同类型的栈,可以用一个数组data[0...MaxSize来实现这两个栈,这称为共享栈。
. 栈空条件:栈1空为top1 == -1;栈2空为top2 == MaxSize
. 栈满条件:top1 == top2 - 1
. 元素x进栈操作:进栈1操作为top++;data[top1] = x;进栈2操作为top2--;data[top2] = x;
. 出栈x操作:出栈1操作为x = data[top1];top1--;出栈2操作为x = data[top2];top2++;

定义结构体
data数组表示共享栈的存储空间,top1和top2分别为两个栈的栈顶指针,这样改共享栈通过data,top1和top2来标识,也可以将它们设计为一个结构体类型:
typedef struct
{
ElemType data[MaxSize];//存放共享栈中的元素
int top1, top2;//两个栈的栈顶指针
}DStack;
1.1.4 链栈
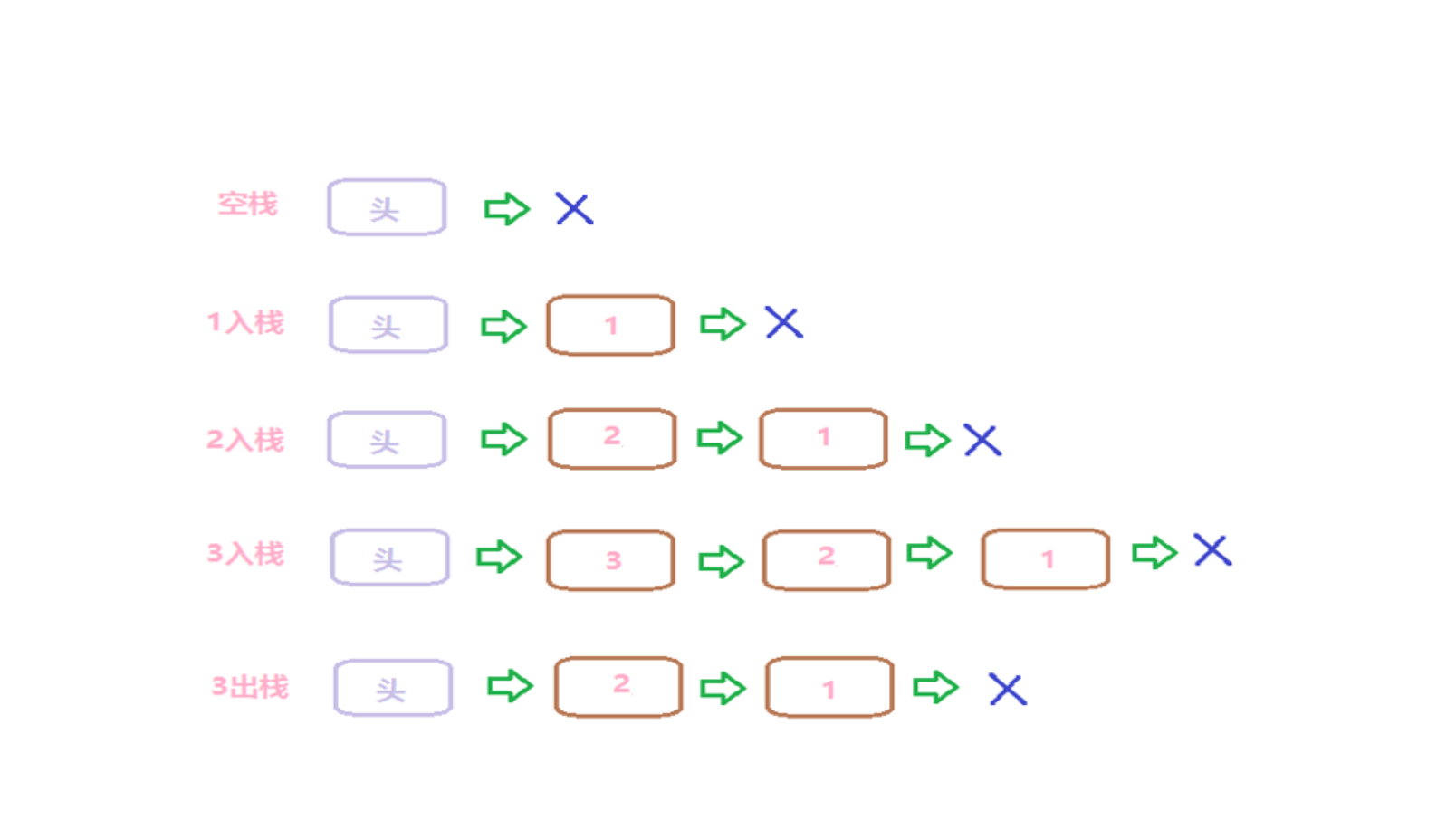
采用链表存储的栈称为链栈,这里采用带头结点的单链表实现。
链栈四要素:
. 栈空的条件:s->next == NULL
. 栈满的条件:由于只有内存溢出时才出现栈满,通常不考虑,所以看作不存在栈满
. 元素e的进栈操作:新建一个结点存放元素e(由p指向它),将结点p插入到头节点之后,头插法
. 出栈操作:取出首结点的data值并将其删除
定义结构体
typedef int ElemType;
typedef struct linknode
{
ElemType data;//数据域
struct linknode* next;//指针域
}LiNode, LiStack;
初始化栈
void InitStack(LiStack &s)
{
s = new LiNode;
s->next = NULL;
}
销毁栈
释放链栈占用的全部空间结点,和单链表的销毁算法相同
void DestroyStack(LiStack& s)
{
LiStack node;
while (s != NULL)
{
node = s;
s = s->next;
delete node;
}
}
判断栈是否为空
栈s为空的条件时s->next=NULL,同空链表
bool StackEmpty(LiStack s)
{
return(s->next==NULL)
}
进栈
新建一个结点,用于存放元素e(由p指向它),然后将其插入头节点之和作为新的首结点
void Push(LiStack& s, ElemType e)
{
liStack p;
p = new Linode;
p->data = e;
p->next = s->next;
s->next = p;
}
出栈
在栈不为空的情况下提取首结点的值赋给参数e,然后将其删除
void Pop(LiStack& s, ElemType& e)
{
LiStack p;
if (s->next == NULL)//栈空
return false;
p = s->next;//p指向开始结点
e = p->data;//取值
s->next = p->next;//删除p结点
delete p;//释放p结点
return true;
}
取栈顶元素
在栈不为空的条件下提取首结点的数据域赋给参数e
void GetTop(LiStack s, ElemType& e)
{
if (s->next == NULL)//栈空
return false;
e = s->next->data;
return true;
}
1.1.5 栈c++模板
#include <stack>///头文件
stack<int>s;//初始化栈,参数表示元素类型
s.push(t);//入栈元素t
s.top();//返回栈顶元素
s.pop();//出栈,物理删除栈顶数据,不返回该元素
s.empty();//栈空时,返回true
s.size();//访问栈中的元素个数
1.2 栈的应用
- 数制转换
- 括号匹配检验
- 迷宫求解
- 表达式求值 & 中缀表达式转后缀表达式
1.3 队列
1.3.1 队列的介绍
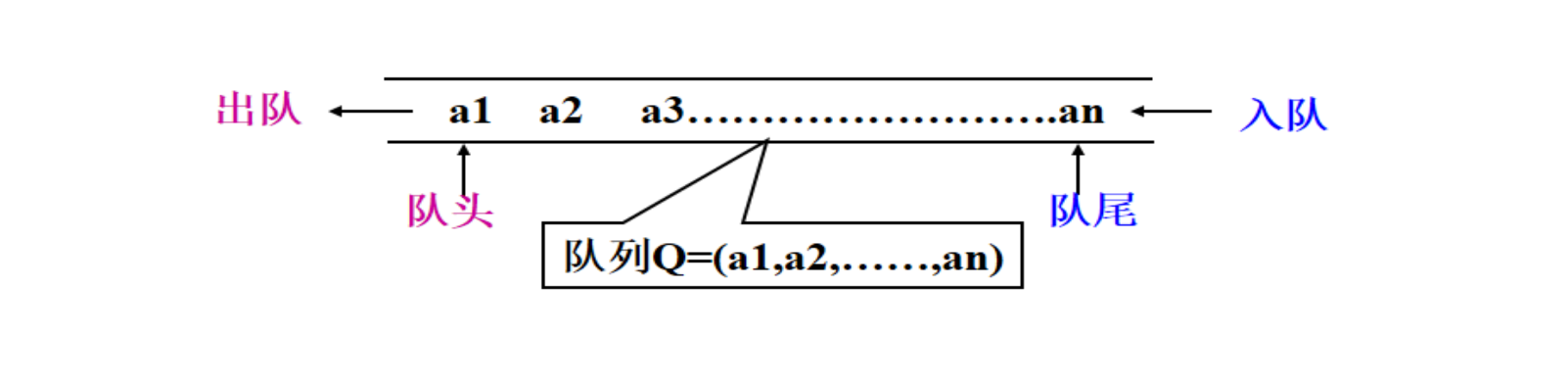
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队,从队列中删除一个队列元素称为出队。因为队列只允许在一端插入,在另一端删除,所以只有最早进入队列的元素才能最先从队列中删除。
特点:先进先出
队尾:允许插入的一端
对头:允许删除的一端
1.3.2 顺序队列
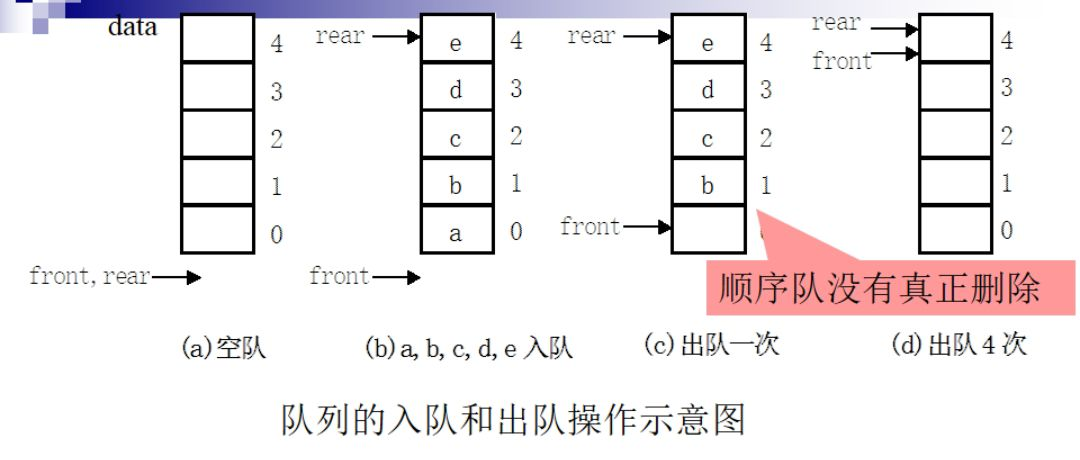
采用顺序存储结构的队列称为顺序队,即分配一块连续的存储空间来存放队列中的元素,并用两个整型变量来反映队列中元素的变化,它们分别储存队首元素和队尾元素的下标位置,分别称为队首指针(队头指针)和队尾指针。

定义结构体
typedef struct
{
ElemType data[MaxSize];
int front, rear;//队首和队尾指针
}Queue;
typedef Queue* SqQueue;
初始化队列
void InitQueue(SqQueue& q)
{
q = new Queue;
q->front = q->rear = -1;
}
销毁队列
void DestroyQueue(SqQueue& q)
{
delete q;
}
判断队列是否为空
bool QueueEmpty(SqQueue q)
{
return(q->front == q->rear);
}
进队列
bool enQueue(SqQueue& q, ElemType e)
{
if (q->rear + 1 == MaxSize)//队满
return false;
q->rear = q->rear + 1;
q->data[q->rear] = e;
return true;
}
出队列
bool deQueue(SqQueue& q, ElemType& e)
{
if (q->front == q->rear)//队空
return false;
q->front = q->front + 1;
e = q->data[q->front];
return true;
}
1.3.3 循环队列
把数组的前端和后端连接起来,形成一个环形的顺序表,即把存储队列元素的表达式从逻辑上看成一个环。
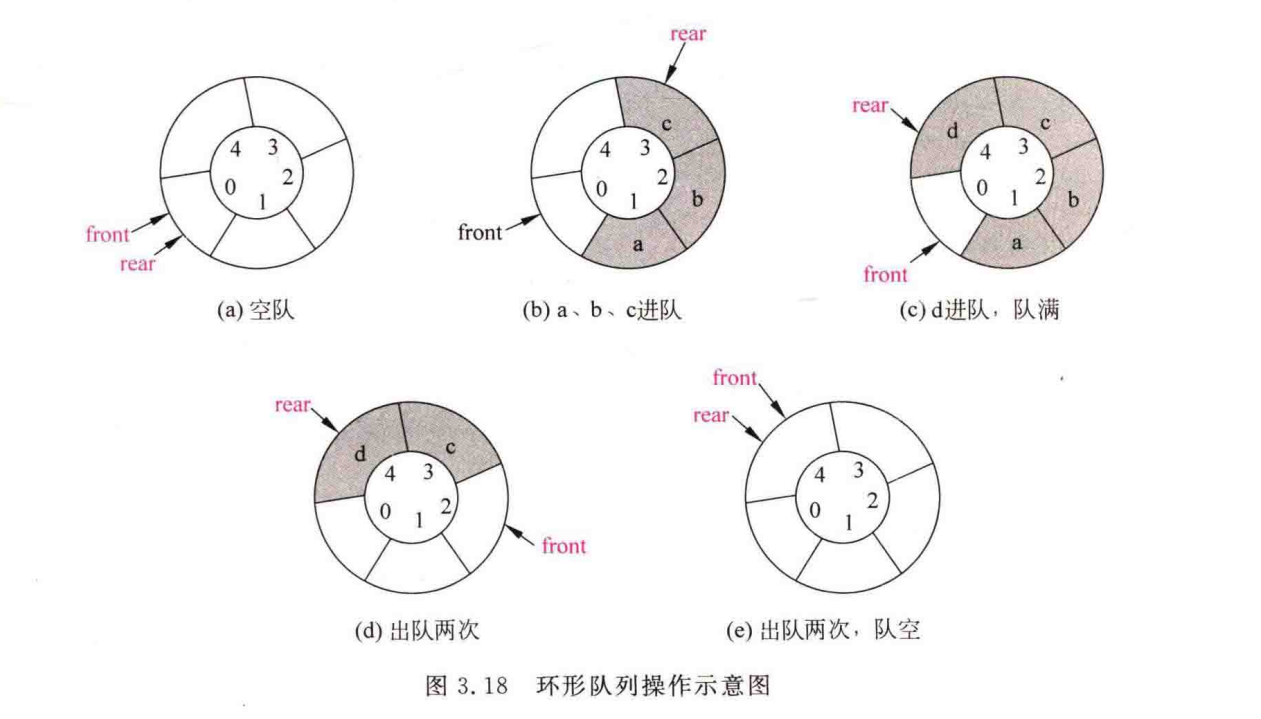
. 队头指针front循环增一:front=(front+1)%MaxSize
. 队尾指针rear循环增一:rear=(rear+1)%MaxSize
. 队空条件:q->rearq->front
. 队满条件:(q->rear+1)%MaxSizeq->front
定义结构体
typedef struct
{
ElemType data[MaxSize];
int front, rear;
}Queue;
typedef Queue* SqQueue;
初始化队列
void InitQueue(SqQueue& q)
{
q = new Queue;
q->front = q->rear = 0;
}
销毁队列
void DestroyQueue(SqQueue& q)
{
delete q;
}
判断队列是否为空
若队列为空,返回真,否则返回假;
bool QueueEmpty(SqQueue q)
{
return(q->front == q->rear);
}
进队列
bool enQueue(SqQueue& q, ElemType e)
{
if ((q->rear + 1) % MaxSize == q->front)//队满
return false;
q->rear = (q->rear + 1) % MaxSize;
q->data[q->rear] = e;
return true;
}
出队列
bool deQueue(SqQueue& q, ElemType& e)
{
if (q->front == q->rear)//队空
return false;
e = q->data[q->front];
q->front = (q->front + 1) % MaxSize;
return true;
}
1.2.4 队列c++模板
#include <queue>///头文件
q.push(x);//x插入队列的末端
q.pop();//弹出队列的第一个元素,物理删除,不返回该元素
q.front();//取队头元素
q.back();//取队尾元素
q.empty();//队列为空时,返回true
q.size();//访问队列中的元素个数
1.2.5 链队列
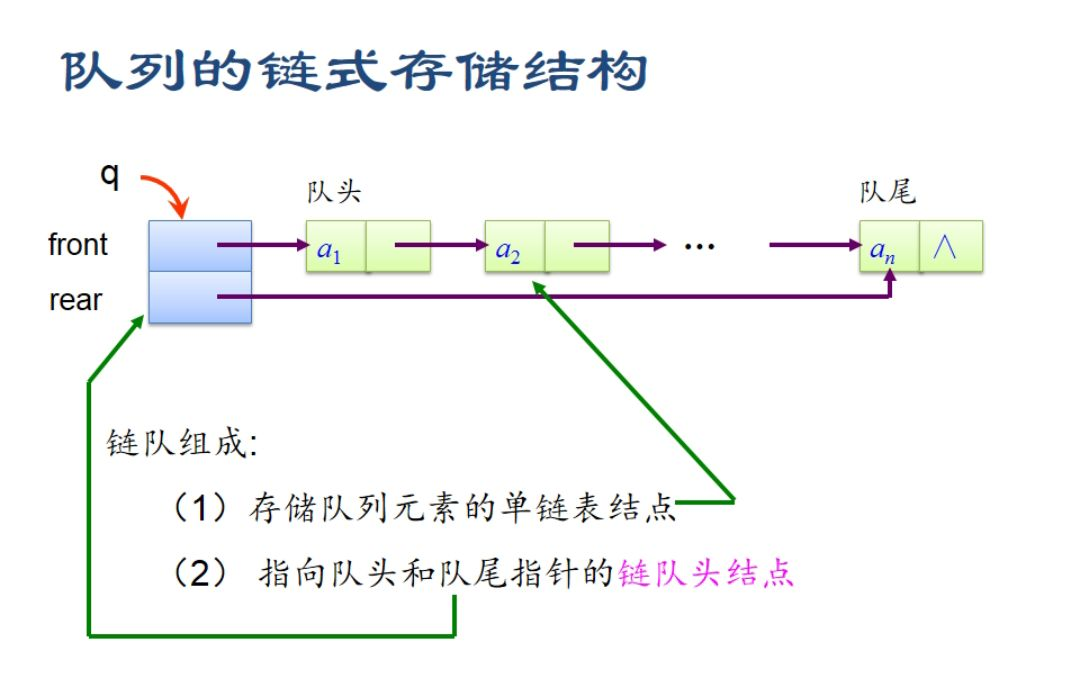
定义结构体
//单链表中数据节点类型QNode定义如下:
typedef struct qnode
{
ElemType data;//数据元素
struct qnode* next;
}QNode;
//链队中头尾指针类型LinkQueue定义如下:
typedef struct
{
QNode* front;
QNode* rear;
}LinkQueue;
初始化链队
构造一个空队,即创建一个链队结点,其front和rear域均置为NULL
Status InitQueue(LinkQueue& Q)
{
Q.front = Q.rear = new QNode;
if (!Q.front) exit(OVERFLOW);
Q.front->next = NULL;
return OK;
}
判断队列是否为空
若队列为空,返回真,否则返回假;
Status QueueEmpty(LinkQueue Q)
{
return(Q.front == Q.rear);
}
求链队列的队头元素
Status GetHead(LinkQueue Q, ElemType& e)
{
if (Q.front == Q.rear)//空队列
return ERROR;
e = Q.front->next->data;
return OK;
}
链队列入队
Status EnQueue(LinkQueue& Q, ElemType e)
{
p = new QNode;
if (!p)exit(OVERFLOW);
p->data = e;
p->next = NULL;
Q.rear->next = p;
Q.rear = p;
return OK;
}
链队列出队
Status DeQueue(LinkQueue& Q, ElemType& e)
{
if (Q.front == Q.rear)//空队列
return ERROR;
p = Q.front->next;
e = p->data;
Q.front->next = p->next;
if (Q.rear == p) Q.rear = Q.front;//最后一个元素被删,改队尾
delete p;
return OK;
}
2.PTA实验作业
2.1 符号配对

#include<stdio.h>
int main()
{
char s[200];
int top = -1;
char c, st[1000];//存储数据
char ch[1000];//用来和栈内符号匹配
ch[')'] = '(';
ch[']'] = '[';
ch['}'] = '{';
int k = 0, flag = 0;
do
{//获取输入数据放入st数组
scanf("%c", &c);
if (flag == 0 && c == '\n')
{
break;
}
st[k++] = c;
if (c == '.')
{
flag = 0;
}
else
{
flag = 1;
}
} while (1);
st[k] = '\0';
for (int i = 0; i < k; i++)
{
if (st[i] == '/')
{
if (i < k&&st[i + 1] == '*')
{
s[++top] = '<';//用<代替/* 入栈
i++;
}
}
else if (st[i] == '(' || st[i] == '[' || st[i] == '{')
{
s[++top] = st[i];//入栈
}
else if (st[i] == '*')
{
if (i < k&&st[i + 1] == '/')
{
if (s[top] == '<')
{ //出栈
i++;
top--;
}
else
{
printf("NO\n");
if (top == -1)
{ //缺失左括号
printf("?-*/\n");
}
else
{ //栈内符号缺失右括号
c = s[top];
printf("%c-?\n", c);
}
return 0;
}
}
}
else if (st[i] == ')' || st[i] == ']' || st[i] == '}')
{
if (s[top] == ch[st[i]])
{ //出栈 用到了ch1数组
top--;
}
else
{
printf("NO\n");
if (top == -1)
{ //缺失左括号
printf("?-%c\n", st[i]);
}
else
{ //栈内符号缺失右括号
c = s[top];
if (c == '<')
{
printf("/*-?\n");
}
else
{
printf("%c-?\n", c);
}
}
return 0;
}
}
}
if (top == -1)
{//当栈为空时,打印yes
printf("YES\n");
}
else
{//剩下的定是缺失右符号的
printf("NO\n");
c = s[top];
if (c == '<')
{
printf("/*-?\n");
}
else
{
printf("%c-?\n", c);
}
}
return 0;
}
2.1.2 知识点总结
. 判断字符为左括号,右括号,以及符号匹配的条件
. 字符栈的应用
2.2 银行业务队列简单模拟

#include<stdio.h>
#include<queue>
#include<iostream>
using namespace std;
int main()
{
int N; cin >> N;
queue<int>que[2];
for (int i = 0; i < N; i++)
{
int temp;cin >> temp;
if (temp % 2 == 1) //分成奇偶队列
que[1].push(temp);
else que[0].push(temp);
}
int flag = 0; //用来控制第一个输出的编号前面不带空格
for (int time = 1;; time++)
{
if (que[0].empty() && que[1].empty())
break;
if (!que[1].empty())
{
if (flag==0)
cout << que[1].front();
else cout << " " << que[1].front();
que[1].pop();flag = 1;
}
if (time % 2 == 0 && !que[0].empty())
{
if (flag==0)cout << que[0].front();
else cout << " " << que[0].front();
que[0].pop(); flag = 1;
}
}
cout << endl;
return 0;
}
2.2.2 知识点总结
. queue模板的应用


 浙公网安备 33010602011771号
浙公网安备 33010602011771号