kmp 与 border 相关
kmp
原来很可爱的家伙居然也可以这么恐怖
P3546 [POI2012]PRE-Prefixuffix
首先一定是对 \(border\) 来求 \(s[i+1,n-i]\) 的 \(border\) 的
考虑这个东西怎么求,设 \(f_i\) 表示答案
把边界缩短 \(1\),可以发现这个 \(f\) 是可以继承的!
掐头去尾后发现中间的部分移动后还是对齐的,那么就有 \(f_{i+1}\ge f_i+2\)
那么倒序去做就可以保证复杂度了
考虑用 \(dp\) 来解决,设 \(f_i\) 表示 \(i\) 这个前缀的答案是多少
那么考虑转移的方向只有 \(i\) 和 \(f_{nxt_i}\),现在需要判断 \((nxt_i,i]\) 这一段是否可以印上
由于最后一段是可以由 \(border\) 来覆盖的,而且这个题目的限制是有区间性的,也就是说假如前缀 \(i\) 对 \(j\) 合法,那么意味着 \(j\) 出现的频率不小于 \(j\)
考虑把前缀的一部分截出来以后,仍然满足这个性质,这就证明了只要有一个 \(k\ge i-nxt_i\) 满足了 \(f_k=f_{nxt_i}\),那么 \((k,i]\) 这一段一定也是可以由 \(f_{nxt_i}\) 覆盖掉的
可以发现这个 \(dp\) 之所以可以设的这么朴素,是因为它和 \(kmp\) 的 \(nxt\) 求解过程具有一定的贴合性,\(border\) 这个东西本来就是可以通过求每个前缀的信息来更新后面的,那么 \(dp\) 数组同样可以
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+5;
int n,nxt[maxn],f[maxn],pos[maxn];
char a[maxn];
int main(){
scanf("%s",a+1);n=strlen(a+1);
for(int i=2,j=0;i<=n;i++){
while(j&&a[i]!=a[j+1])j=nxt[j];
if(a[i]==a[j+1])j++;
nxt[i]=j;
}
f[1]=pos[1]=1;
for(int i=2;i<=n;i++){
if(pos[f[nxt[i]]]>=i-nxt[i])f[i]=f[nxt[i]];
else f[i]=i;
pos[f[i]]=i;
}
cout<<f[n];
return 0;
}
考虑问题可以化归为问题“在 \(S[1,j]\) 前面拼上 \(T[1,i]\) 后的 \((出现次数,匹配位置)\)”
考虑现在主要的问题是跨过边界的部分怎样计算
考虑先不管 \(S\) 具体的匹配过程,只看 \(T\),那么在做 \(kmp\) 过程中会一直跳 \(nxt\),而跳的这部分是就是 \(T[1,i]\)
考虑我们只关心每次失配时 \(T\) 的修改过程,并且预处理出这中间产生的答案的个数,最后再加上一直不失配的一段的答案
答案个数可以用 \(kmp\) 上的前缀和解决,即计算每个 \(T\) 在做 \(kmp\) 的时候产生的匹配 \(S\) 前缀的次数
然后还需要求出 \(T\) 的跳父亲什么时候结束,这个位置一定位置一定满足 \(lcp(T[i+1,len_t],S)\ge len\),这个 \(lcp\) 的形式是经典的 \(exkmp\) 问题,可以做到预处理后 \(O(1)\) 判断
然后倍增跳跃,保存这一段最长 \(lcp\) 即可
这道题看似居然可以实现区间拼接求出现次数,但是这个前缀的独特性使得其可以在 \(T\) 的 \(kmp\) 自动机上进行匹配
其关键转化是摆脱 \(T\) 和 \(S\) 具体的匹配过程,而是去关心 \(T\) 上的 \(border\) 的变化
代码
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define int long long
typedef pair<int,int>pi;
const int maxn=5e5+5;
int n,m,t,q,k,nxt[maxn],e_nxt[maxn],h[maxn],ans[maxn],tot[maxn],cur[maxn],pos[maxn],l,r,sum[maxn];
int f[maxn][22],g[maxn][22],pre[maxn];
char a[maxn],b[maxn];
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void exkmp(){
e_nxt[1]=m;
for(int i=2,l=0,r=0;i<=n;i++){
if(r>=i)e_nxt[i]=min(e_nxt[l-i+1],r-i+1);
while(i+e_nxt[i]<=n&&a[i+e_nxt[i]]==a[e_nxt[i]+1])e_nxt[i]++;
if(i+e_nxt[i]-1>r)r=i+e_nxt[i]-1,l=i;
}
for(int i=1,l=0,r=0;i<=m;i++){
if(r>=i)h[i]=min(h[l-i+1],r-i+1);
while(i+h[i]<=m&&b[i+h[i]]==a[h[i]+1])h[i]++;
if(i+h[i]-1>r)r=i+h[i]-1,l=i;
}
for(int i=1;i<=m;i++)h[i]=h[i+1];
}
void kmp(){
sum[1]=(h[1]==m-1);
for(int i=2,j=0;i<=m;i++){
while(j&&b[i]!=b[j+1])j=nxt[j];
if(b[i]==b[j+1])j++;
nxt[i]=j;sum[i]=sum[nxt[i]]+(h[i]==m-i);
}
for(int i=1;i<=m;i++){
f[i][0]=nxt[i];g[i][0]=h[i];
for(int j=1;j<=t;j++){
f[i][j]=f[f[i][j-1]][j-1];
g[i][j]=max(g[i][j-1],g[f[i][j-1]][j-1]);
}
}
for(int i=1,j=0;i<=n;i++){
while(j&&a[i]!=b[j+1])j=nxt[j];
if(a[i]==b[j+1])j++;
pre[i]=pre[i-1]+(j==m);
if(j==m)j=nxt[j];cur[i]=j;
}
// for(int i=1;i<=n;i++)cout<<cur[i]<<" ";puts("");
}
pi insert(int x,int len){
int res=sum[x];
for(int i=t;i>=0;i--)if(g[x][i]<len)x=f[x][i];
if(h[x]<len)x=nxt[x];
// cout<<"ppp "<<x<<endl;
if(!x)return {res+pre[len],cur[len]};
res-=sum[x];x+=len;
if(x==m)x=nxt[x],res++;
return {res,x};
}
int ask(int x){
int now=lower_bound(tot+1,tot+k+1,x)-tot-1;
return ans[now]+insert(pos[now],x-tot[now]).fi;
}
signed main(){
freopen("youl.in","r",stdin);freopen("youl.out","w",stdout);
scanf("%s%s",a+1,b+1);n=strlen(a+1),m=strlen(b+1);
t=log2(m)+1;exkmp();kmp();k=read();
for(int i=1,x;i<=k;i++){
tot[i]=tot[i-1]+(x=read());
pi res=insert(pos[i-1],x);
// cout<<"hhh "<<res.fi<<" "<<res.se<<endl;
pos[i]=res.se;ans[i]=ans[i-1]+res.fi;
}
q=read();
for(int i=1;i<=q;i++){
l=read(),r=read();
if(r-l+1<m)puts("0");
else printf("%lld\n",ask(r)-ask(l+m-2));
}
return 0;
}
考虑在 \(k\times (AB)\) 的位置上统计答案,其实这个东西是可以\(O(1)\) \(check\) 的,因为相当于要判断 \(\frac{i}{k}\) 是否是前缀 \(i\) 的周期,那么同理也就是要判断是否为 \(border\) 即可,因此直接判断 \(i-nxt_i|\frac{i}{k}\)
对于后面部分 \(A\) 最长部分能到达多远是一个 \(lcp\) 问题,用扩展 \(kmp\) 来求解即可
另外在一些情境下 \(kmp\) 会配合 \(dp\),但是都很自然,顺着题意模拟即可
比如远古场 \(FSYO\) 模拟赛中出现过
扩展 kmp
首先定义 \(Z\) 函数表示后缀 \(i\) 与整个串的 \(lcp\) 长度
一个比较好的理解于实现方式是类似于 \(manacher\) 维护出 \([l,r]\) 表示能够匹配的最右端是 \(l\) 位置匹配上的到达 \(r\) 的区间
假设目前求到 \(i\),先画张图:
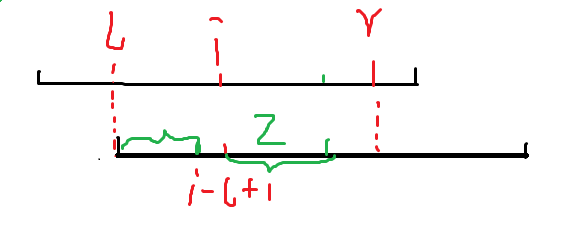
那么可以发现可以直接由 \(nxt[i-l+1]\) 继承过来,需要和 \(r-i+1\) 取 \(min\)
另一个问题是假如 \(r<i\) 或 \(nxt[i-l+1]\ge r-i+1\),后面的部分需要进行暴力匹配
并且及时更新 \(r\) 的取值
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e7+5;
int n,m,nxt[maxn],ex[maxn];
char a[maxn],b[maxn];
long long ans;
void getnxt(){
nxt[1]=m;
for(int i=2,l=0,r=0;i<=m;i++){
if(i<=r)nxt[i]=min(nxt[i-l+1],r-i+1);
while(i+nxt[i]<=m&&b[nxt[i]+i]==b[nxt[i]+1])nxt[i]++;
if(i+nxt[i]-1>r)r=i+nxt[i]-1,l=i;
}
return ;
}
void exkmp(){
for(int i=1,l=0,r=0;i<=n;i++){
if(i<=r)ex[i]=min(nxt[i-l+1],r-i+1);
while(i+ex[i]<=n&&a[ex[i]+i]==b[ex[i]+1])ex[i]++;
if(i+ex[i]-1>r)l=i,r=i+ex[i]-1;
}
return ;
}
int main(){
scanf("%s%s",a+1,b+1);
n=strlen(a+1),m=strlen(b+1);
getnxt();exkmp();
for(int i=1;i<=m;i++)ans^=1ll*i*(nxt[i]+1);cout<<ans<<endl;//printf("%d ",nxt[i]);puts("");
ans=0;for(int i=1;i<=n;i++)ans^=1ll*i*(ex[i]+1);cout<<ans;
return 0;
}
相当于比较每个后缀的 \(nxt\) 值是否等于后缀长度
由于需要求出现的次数,不妨还是把后缀们平移到前缀的位置
那么发现一个前缀出现的次数是后面前缀出现次数的前缀和
相当于对于每个后缀 \(i\),前缀 \(1\sim nxt_i\) 都在这个位置 \(i\) 出现过
这种方法让我们可以 \(O(n)\) 求出每个前/后缀在整个串中的出现个数
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
char a[maxn];
int nxt[maxn],ans,cnt[maxn];
bool vis[maxn];
int main(){
scanf("%s",a+1);
int n=strlen(a+1);
nxt[1]=n;
for(int i=2,l=0,r=0;i<=n;i++){
if(i<=r)nxt[i]=min(nxt[i-l+1],r-i+1);
while(nxt[i]+i<=n&&a[nxt[i]+i]==a[nxt[i]+1])nxt[i]++;
if(nxt[i]+i-1>r)r=nxt[i]+i-1,l=i;
}
for(int i=1;i<=n;i++){
if(i+nxt[i]-1==n)ans++,vis[nxt[i]]=true;
cnt[nxt[i]]++;
}
for(int i=n;i>=1;i--)cnt[i]+=cnt[i+1];
cout<<ans<<endl;
for(int i=1;i<=n;i++)if(vis[i])printf("%d %d\n",i,cnt[i]);
return 0;
}
CF1313E Concatenation with intersection
首先考虑把有交的条件只用 \(l1,r2\) 来刻画,此时只需要满足 \(r2\le l1+m-2\) 即可
设 \(fa_i,fb_i\) 表示后缀 \(i\) 的 \(lcp\),以及前缀 \(i\) 的 \(lcs\),可以用 \(exkmp\) 求出
此时对于固定的 \(l1,r2\) 答案是 \(max(fa_{l1}+fb_{r2}-m+1,0)\)
把 \(max\) 拆开后对于固定的 \(l_1\) 维护 \(r_2\) 个数和 \(fb_{r2}\) 和即可
可以用双指针+树状数组实现
border 理论
字符串最本源的东西——\(border\) 居然可以有这样深奥的理论
首先是定义,\(border\) 指能与后缀匹配的前缀长度
周期:设周期为 \(s\),所有 \(i\) 满足 \(a[i]=a[s+i]\)
这里注意周期并不代表一定能整除 \(n\),即匹配完全,只是一个 \(border\) 顺带的性质
以下是一些结论,大部分省略证明:
- \(Bd(S)=mxBd(S)+Bd(mxBd(S))\)
类似于跳 \(nxt\) 的过程,用于求出所有 \(border\)
有时候为了快速跳,可以建立出失配树
两个前缀的公共 \(border\) 是失配树上的 \(lca\)
- 弱周期引理:若 \(p\) 和 \(q\) 都是 \(S\) 的周期,且 \(p+q\le n\) 那么 \(gcd(p,q)\) 也是 \(S\) 的周期
这个的证明可以采用类似于辗转相除的方式验证
注意 \(p+q\le n\) 的限制不能少
-
若 \(S\) 是 \(T\) 的前缀,且 \(T\) 有周期 \(a\) ,\(S\) 有整周期 \(b\) ,\(b|a\),\(|S|\ge a\) ,则 \(T\) 也有周期 \(b\)
-
若 \(2|S|\ge |T|\),\(S\) 在 \(T\) 中的匹配位置必为等差序列
-
\(S\) 的长度达到 \(n/2\) 的 \(Bd\) 长度构成一个等差序列
-
一个串 \(S\) 的所有 \(Bd\) 按长度排序后,可以被划分成 \(O(logn)\) 个等差序列
P3538 [POI2012]OKR-A Horrible Poem
思路完全想偏了……这种区间的题貌似不太能用 \(kmp\) 式的 \(border\) 自动化实现吧
首先由于周期是可以 \(O(1)\) 判断的,即判断是否为 \(border\),那么考虑直接枚举周期的长度
周期肯定都是 \(len\) 的约数,并且有约数单调性,即 \(kx\) 如果不满足,那么 \(x\) 一定不满足
那么不必枚举约数,直接试除每一个质因子就好了,复杂度降为 \(nlogn\)
代码
#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
const int maxn=5e5+5,base=131;
int n,m,vis[maxn],pri[maxn],cnt,l,r;
ull sum[maxn],po[maxn];
char a[maxn];
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
ull calc(int l,int r){return sum[r]-sum[l-1]*po[r-l+1];}
void pre(){
for(int i=2;i<=n;i++){
if(!vis[i])vis[i]=pri[++cnt]=i;
for(int j=1,x;j<=cnt;j++){
if((x=pri[j]*i)>n||pri[j]>vis[i])break;
vis[x]=pri[j];
}
}
po[0]=1;for(int i=1;i<=n;i++)sum[i]=sum[i-1]*base+a[i],po[i]=po[i-1]*base;
}
bool check(int l,int r,int len){//[l,r]中len是否为周期
return calc(l,r-len)==calc(l+len,r);
}
int ask(int l,int r){
int len=r-l+1,res=len;
while(len!=1){
if(check(l,r,res/vis[len]))res/=vis[len];
len/=vis[len];
}
return res;
}
int main(){
n=read();scanf("%s",a+1);pre();m=read();
for(int i=1;i<=m;i++)l=read(),r=read(),printf("%d\n",ask(l,r));
return 0;
}
CF1286E Fedya the Potter Strikes Back
考虑加入最后一个字符以后目前的 \(border\) 会发生哪些变化
首先会加入一个长度为 \(1\) 的 \(border\),剩下的长度 \(+1\) 或者消失掉
可以发现所有下一个字符不是新加入的这个字符的 \(border\) 会消失掉
现在问题在于怎样又快又准地找到这些消失掉的 \(border\)
可以维护一个 \(fa_i\) 表示 \(fail\) 树上第一个和这个节点后面一个节点不同的祖先
那么从当前节点出发,如果其颜色匹配上了,就跳 \(fa_i\),否则就跳 \(nxt_i\),这样可以保证在两步跳跃之中至少删除一个节点
然后就是维护上的问题了,支持加删,全局取 \(min\),求和,用 \(map\) 实现即可
动态查找权值用二分栈解决
代码
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define int __int128
typedef pair<int,int>pi;
const int maxn=6e5+5;
int n,w[maxn],a[maxn],nxt[maxn],fa[maxn];
int sum,ans[maxn];
char c[5];
vector<int>sta;
map<int,int>s;
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void insert(int x){
if(a[1]==a[x])s[w[x]]++,sum+=w[x];
while(sta.size()&&w[sta.back()]>w[x])sta.pop_back();
sta.pb(x);
}
void erase(int x){
// cout<<"kkk "<<x<<endl;
int cur=w[*lower_bound(sta.begin(),sta.end(),x)];
if(!--s[cur])s.erase(s.find(cur));sum-=cur;
}
void push(int w){
for(auto it=s.upper_bound(w);it!=s.end();it=s.erase(it))s[w]+=it->se,sum-=(it->fi-w)*it->se;
}
void insert(int c,int &j,int i){
while(j&&a[j+1]!=c)j=nxt[j];nxt[i]=(j+=(a[j+1]==c));
fa[i-1]=(a[nxt[i-1]+1]==c?fa[nxt[i-1]]:nxt[i-1]);
int x=i-1;
while(x){
// cout<<"ppp "<<x<<" "<<a[x+1]<<" "<<c<<endl;
if(a[x+1]!=c)erase(i-x),x=nxt[x];
else x=fa[x];
// cout<<"kkk "<<x<<" "<<fa[x]<<" "<<nxt[x]<<endl;
}
push(w[i]);insert(i);
}
void print(int x){
if(x<=9)return putchar(x+'0'),void();
print(x/10);print(x%10);
}
signed main(){
n=read();scanf("%s",c+1);a[1]=c[1]-'a';
w[1]=read();insert(1);print(ans[1]=sum);puts("");
for(int i=2,j=0;i<=n;i++){
scanf("%s",c+1);w[i]=read()^(ans[i-1]&((1<<30)-1));
c[1]=(c[1]-'a'+ans[i-1])%26;
insert(a[i]=c[1],j,i);
print(ans[i]=ans[i-1]+sum);puts("");
// printf("%lld\n",ans[i]=ans[i-1]+sum);
// cout<<"hhh "<<nxt[i]<<" "<<fa[i]<<endl;
}
// for(int i=1;i<=n;i++)putchar(a[i]+'a');puts("");
// for(int i=1;i<=n;i++)cout<<w[i]<<" ";puts("");
return 0;
}
考虑点分治,那么一个回文串被分成了两部分,把较短的那部分放入 \(AC\) 自动机,然后对于剩余那边一定是 \(log\) 个等差数列回文前缀,那对于每个等差数列根号分治后查询即可
这种点分治上带根号的貌似复杂度都是 \(n\sqrt{n}\)?


 浙公网安备 33010602011771号
浙公网安备 33010602011771号