树基础

树，作为一种神奇的结构，除了用树剖倍增等高端方法维护外，常常用一些小技巧即可达到目的

一些题的建树会隐藏起来，一般会有“区间只有包含关系”、“只有一种路径可以到达”等

---

dfs 序

$dfs$ 序一般指遍历到一个点以及离开时都入栈形成的序列，在一些情况下回溯时可以不入栈

$dfs$ 用于子树加或子树询问可谓得天独厚，与树状数组结合可以大大降低码量和常数
同时还可以做树链+单点操作（任意一个修改另一个查询均可），都是要把树链转化为单点差分，单点转化为子树查询

除此之外，$dfs$ 序可以用于判断祖孙关系
一棵树上判断两个点是否是祖孙关系，只要看一个点是不是被包含在另一个点的 $dfs$ 序区间即可

---

P3605 [USACO17JAN]Promotion Counting P

又是一个询问子树内信息的题，那么很自然的想到用 $dfs$ 来维护

---

有一种利用 $dfs$ 序的关键点统计问题，即树上有一些关键点，往往取 $dfs$ 序相邻两个进行计算最优或满足条件
那么把这些关键点按照 $dfn$ 放进 $set$ 里，每次插入时对于相邻的数分别计算贡献即可
这个类似于虚树的技巧

---

P3320 [SDOI2015]寻宝游戏

这道题显然按照 $dfs$ 序的相邻关系遍历所有关键点得到的答案是最优的
动态插入删除即可

---

E. 七彩树

在这道题中，关键点变成了每种颜色的所有点，那么同种颜色会算重在 $lca$ 的地方，那么维护 $set$ 中相邻两点的 $lca$ 减法即可

具体见 这里，同时启发我们这种情境可以用离线的线段树和并与树状数组实现

---

边与点

CF1280C Jeremy Bearimy

这种对每条边算贡献的题似乎很常见
最小值在子树内匹配，不需要关心具体的配对关系，只需要根据奇偶判断有没有即可
最大值在子树外匹配，不需要关心具体的配对关系，只需要根据大小判断有多少即可

---

P4643 [国家集训队]阿狸和桃子的游戏

非常巧妙的题
考虑一条 $(u,v)$ 且权值为 $w$，把 $w/2$ 分别给 $u$ 和 $v$
证明一下正确性：
加入 $u$ 和 $v$ 分别被两个人选，那么 $a-b=(a+w/2)-(b+w/2)$
如果归一个人选，那么 $a+b+w=(a+w/2)+(b+w/2)$

---

P2151 [SDOI2009]HH去散步

可以发现按照原来的说法并不能刻画出“刚走过的边不能重复走”的条件
那么如果把边点互换，发现只有走到一个新的点才算，就可以刻画了

---

LCA

当然一般树剖足够
如果真有卡 $log$ 的，再记录两种做法

---

rmp求LCA

首先写出来 $dfs$ 序，注意这里的 $dfs$ 要求每个儿子回溯回来都要入栈一次
那么两点间的 $LCA$ 就是 $dfs$ 序上两点间深度最小的点，$RMQ$ 预处理即可

一种不用记录两倍的方式是每次进入和出子树的时候都把父亲加入序列，那么此时计算 $[pos_a+1,pos_b]$ 即可

毒瘤的 $cyh$ 曾尝试卡四毛子求 $RMQ$ ……

---

tarjan LCA

从根开始 $dfs$，标记当前节点的祖先节点和已经回溯的节点
回溯时将当前节点并查集的 $fa$ 指向父亲节点
那么每个节点回溯时处理有关询问，如果另一个点已经完成回溯，那么其并查集的祖先就是 $LCA$
需要离线，复杂度 $O(n)$

---

一类拆分路径的 $LCA$ 问题

这个类型在 树剖 里也写了……

B. 牛半仙的妹子Tree

写出表达式，假如在 $t$ 时刻能由 $t'$ 时刻的 $v$ 传染过来，那么需要满足：

$$dep_u+dep_v-2dep_{lca}\le t-t'$$

$$dep_v+t'-2dep_{lca}\le t-dep_u$$

考虑把左边的式子在询问的时候直接做
那么可以对于从 $v$ 到根的每个节点加上 $dep_v+t'$，会发现 $lca$ 比较烦人，其实直接在树剖建树的时候直接设为 $-2dep_u$ 即可

---

P4211 [LNOI2014]LCA

一个点的 $dep$ 就是这个点到根上的节点个数
那么从而可以把一个点 $dep$ 的贡献通过对 $i$ 到根的所有点加 $1$ 来体现
具体地，把询问差分，那么每个询问修改都只操作从 $x$ 到根路径上的点即可

---

包括 这道题，详见 这里

---

重心

重心指所有子树（以及父亲）的大小都小于 $n/2$ 的点
一棵树的重心只可能有 $1$ 个或 $2$ 个

求取重心的过程直接模拟出最大的子树大小即可

---

AT2673 [AGC018D] Tree and Hamilton Path

还是钦定一条边看经过这条边的次数算贡献
假如是个回路，那么对于一条边，然后强制两端的连通块内的点往返连边，这样一定是最优的
至于连边的顺序是怎样不需要关心
然而要求哈密顿路径，那么可以先求回路然后减去一条边即可
至于这条边是哪条，一个结论是一定经过重心！
那么删去经过重心的最短距离路径即可（如果重心有两个则是它们之间的）

---

P5666 [CSP-S2019] 树的重心

考虑一种倍增求重心的方法
一个子树内的重心，可以由这个点一直跳重儿子知道满足大小条件
那么 $dfs$ 时换根，对于每一个儿子 $v$ 求一个重心，其余的再求一个重心
由于儿子可能是重儿子，那么需要记录次儿子来倍增

---

数据结构

题意大概是说带修动态求带权重心之类的

根据重心的性质，其子树大小小于一半，那么重心的子树一定包含了 $dfs$ 上的带权中点
那么此时从带权中点向上倍增寻找重心即可

---

直径

首先是对直径保持敏感，树内最长路径、树内距一个点的最远点等问题要注意考虑直径

求直径有两种常见方法：

• 两遍 $dfs$

从任意一个点为根 $dfs$ 出距离最远点，再从最远点 $dfs$ 出一个最远点，那么至两个点就是直径的两端点

• 树形 $dp$

$dp$ 出子树内到根的最长路径，然后拼接即可

---

P1099 [NOIP2007 提高组] 树网的核

答案路径一定在直径上，不妨随意设一条直径上进行尺取
对于一条直径上的一段路径，最远距离有两种情况，当前直径两端点与路径两端点的距离，以及其他点的距离

至于为什么其他点有机会贡献最大值，可以画个图理解一下：

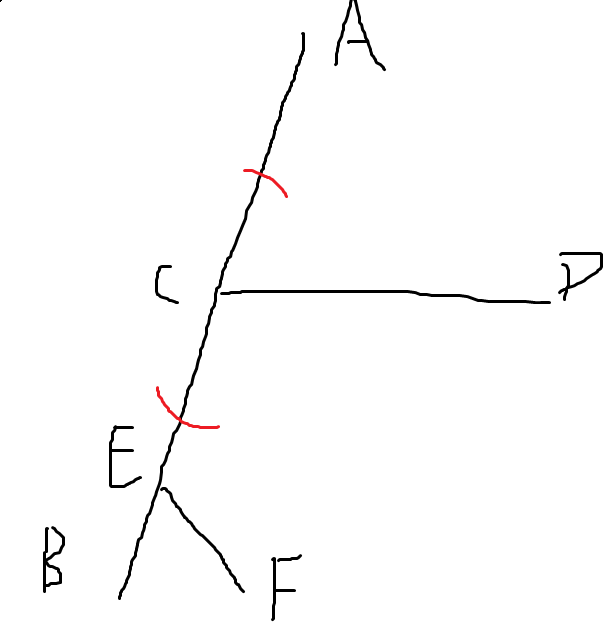
比如 $AB$ 为直径，那么直径的贡献并没有 $CD$ 多
那这个贡献只要计算所有点与直径距离的最大值即可
这样算的原因是假如 $EF$ 的距离很大，但其实不会造成贡献，因为直径的性质一定没有 $BE$ 长

---

AT4133 [ARC097D] Monochrome Cat

假如选定一个环，那么遍历完一棵树答案是固定的
唯一有问题的选择的是一条路径，那么会使得少经过的路上的点发生变化
那么可以先处理出环时的答案，发现黑白点对应的权值可以重新定义了
此时要找的相当于就是一条最长直径，树形 $dp$ 即可

---

直径可以动态维护，比如用并查集和线段树等
数据结构里记录当前连通块的直径两端点，合并时新的直径一定是这四个点中的两个，枚举判断即可