noip模拟41
A. 你相信引力吗
很明显的单调栈的题,考场上没有想到平移最大值,而是想着复制一倍序列破环成链,然后发现最大值的部分特别难维护,而且耗费时间过长,只好牺牲时间复杂度加了个 去重。
首先把一个最大值放到最左边,这样除了最大值都不能跨过左端点走另一半的环进行匹配
然后维护单调不增栈,对于多个连续值维护当前是第几个,往后递推即可
过程中需要特判最大值防止算重
代码实现
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e7+5;
int n,a[maxn],mxpos,sta[maxn],f[maxn],tp;
long long ans;
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i+n]=a[i]=read();
if(a[i]>a[mxpos])mxpos=i;
}
for(int i=mxpos;i<mxpos+n;i++){
while(tp&&a[sta[tp]]<a[i])ans++,tp--;
if(a[sta[tp]]>a[i])ans++;
else ans+=f[sta[tp]]+(a[i]!=a[mxpos]);
sta[++tp]=i;
f[i]=(a[i]==a[sta[tp-1]])?f[sta[tp-1]]+1:1;
}
while(tp>2){
if(a[sta[tp]]==a[sta[2]])break;
tp--;
ans++;
}
cout<<ans;
return 0;
}
B. marshland
考虑网络流:
如果把格子黑白染色,那么一个有危险值的格子流量为 ,但是费用流并不能控制其恰好为 ,可能会出现流量为 但费用算入贡献的情况
那么可以按如下方法染色:

将棋盘染成类似上述三种颜色:
那么一种合法的方案一定由蓝到红再到黄(假定红色是危险的格子)
那么把红色格子拆点放在中间,连一条费用为危险值的边,蓝色作为左边点,原点向其连边,然后连向中间入点;黄色点放右边,从出点向其连边,然后连向汇点
注意这道题要求可行流,比起传统费用流来讲并不是有流就流,而是当前路径费用为正才流
C. party?
特产的选择方案比较奇怪,可以用网络流维护
这其实是一个二分图,左部点是 个人,每个人相当于拥有 的流量,然后每个人向其对应特产连边,特产流量为一
现在要计算满足满流的最大流量
根据 定理,二分图存在完美匹配当且仅当对于任意的 ,左部任意 个点在右边的相邻点个数大于等于
由于 很小,直接枚举所有情况即可
对于统计一条路径上特产有哪些,可以开一个 ,并用树剖维护
为了防止跳链浪费时间,树剖时对于完整的重链记录其所达特产,只在最后一部分线段树上查询
代码实现
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e5+5;
const int len=1005;
const int inf=0x3f3f3f3f;
int n,m,id[maxn],fa[maxn],x,dep[maxn],siz[maxn],son[maxn],re[maxn],tp[maxn],tot,num,pos[maxn],q,hd[maxn],cnt,c[maxn];
bitset<len>col[maxn],S[10];
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
struct Edge{
int nxt,to;
}edge[maxn];
void add(int u,int v){
edge[++cnt].nxt=hd[u];
edge[cnt].to=v;
hd[u]=cnt;
return ;
}
void dfs(int u){
siz[u]=1;
for(int i=hd[u];i;i=edge[i].nxt){
int v=edge[i].to;
dep[v]=dep[u]+1;
dfs(v);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]])son[u]=v;
}
return ;
}
void dfs1(int u,int top){
tp[u]=top;
id[u]=++tot;
re[tot]=u;
if(u!=top)col[u]=col[fa[u]];
col[u].set(c[u]);//(1<<c[u]);
// cout<<u<<" "<<col[u]<<endl;
if(son[u])dfs1(son[u],top);
for(int i=hd[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==son[u])continue;
dfs1(v,v);
}
return ;
}
int lca(int x,int y){
while(tp[x]!=tp[y]){
if(dep[tp[x]]<dep[tp[y]])swap(x,y);
x=fa[tp[x]];
}
if(dep[x]<dep[y])swap(x,y);
return y;
}
struct Seg{
int l,r;
bitset<len>sc;
}t[maxn*4];
void update(int p){
t[p].sc|=t[p<<1].sc|t[p<<1|1].sc;
return ;
}
void build(int p,int l,int r){
t[p].l=l;
t[p].r=r;
if(l==r){
t[p].sc.set(c[re[l]]);
// t[p].sc|=(1<<c[re[l]]);
return ;
}
int mid=l+r>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
update(p);
return ;
}
bitset<len>ask(int p,int l,int r){
if(t[p].l>=l&&t[p].r<=r){
return t[p].sc;
}
int mid=t[p].l+t[p].r>>1;
bitset<len>ans;
if(l<=mid)ans=ask(p<<1,l,r);
if(r>mid)ans|=ask(p<<1|1,l,r);
return ans;
}
bitset<len>que(int x,int ed){
bitset<len>ans;
while(tp[x]!=tp[ed]){
ans|=col[x];
x=fa[tp[x]];
}
ans|=ask(1,id[ed],id[x]);
return ans;
}
int main(){
n=read();
m=read();
q=read();
for(int i=2;i<=n;i++){
fa[i]=read();
add(fa[i],i);
}
for(int i=1;i<=n;i++)c[i]=read();
dfs(1);
dfs1(1,1);
// for(int i=1;i<=n;i++)cout<<col[i]<<endl;
build(1,1,n);
for(int i=1;i<=q;i++){
num=read();
int d;
for(int j=1;j<=num;j++){
if(j==1)d=pos[j]=read();
else d=lca(d,pos[j]=read());
}
for(int j=1;j<=num;j++){
S[j]=que(pos[j],d);
// cout<<S[j]<<endl;
}
tot=inf;
for(int T=1;T<=(1<<num)-1;T++){
bitset<len>sum;
int pnum=0;
for(int j=1;j<=num;j++){
if(T&(1<<(j-1))){
pnum++;
sum|=S[j];
}
}
int x=sum.count();
tot=min(tot,x/pnum);
}
for(int j=1;j<=num;j++)S[j].reset();
printf("%d\n",tot*num);
}
return 0;
}
D. 半夜
首先题意转化为将 串复制一倍,没一个子串与 串的
暴力
复习一下 转移方程式为
考虑优化:
设
很明显有 可以推出
同理 推出
那么发现 的转移有分解点 和 表示:
那么推出下图(盗图 这篇博客):
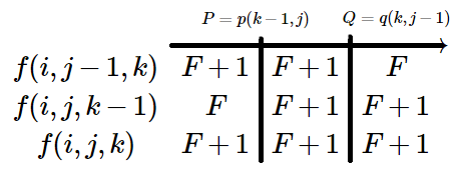
这是 且 的情况,设 根据递推式推出前两行,取 推出第三行,发现 ,
所有 的情况和这个相同
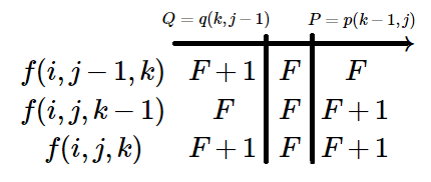
这是 的情况,同理推出 ,
这样两个分界点数组可以递推出来,然后实现 转移
代码实现
#include<bits/stdc++.h>
using namespace std;
const int maxn=4005;
char a[maxn],b[maxn];
int n,p[maxn][maxn],q[maxn][maxn],sum,ans;
int main(){
cin>>n;
scanf("%s",a+1);
scanf("%s",b+1);
for(int i=1;i<=n;i++)a[i+n]=a[i];
for(int i=1;i<=n*2;i++)p[i][0]=i+1,q[i][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=n*2;j++){
int P=p[j][i-1],Q=q[j-1][i];
if(a[j]!=b[i]&&P>Q){
p[j][i]=P,q[j][i]=Q;
}
else p[j][i]=Q,q[j][i]=P;
}
}
for(int i=1;i<=n;i++){
sum=0;
for(int j=i;j<n+i;j++){
if(i>=p[j][n])sum++;
}
ans=max(ans,sum);
}
cout<<ans;
return 0;
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】