特殊的图
竞赛图
定义：任意两点之间都有连边的有向图
性质1：缩点后成链状，拓扑序小的快指向大的块（注意这里的链并不是指严格的入出度都为 \(1\) 的形态，而是指其有严格顺序，没有分叉形态）
性质2：强联通块中存在一条哈密顿回路
性质3：整张竞赛图存在一条哈密顿路径
性质3.5：大小 \(n>1\) 的强联通块中，大小为 [3,n] 的简单环均存在
判定定理：令 \(s_i\) 表示第 \(i\) 个点的出度，排序后若满足 \(\sum_{i=1}^{k} s_i\le \binom{k}{2}\)，且 \(\sum s_i=\binom{n}{2}\)
首先根据竞赛图的性质，缩完点后一定形成了一条链，那么最终要求的即为链上点的个数
缩完点的图一个块是不好刻画的，那么不妨统计前缀的个数，因为这样就满足这个集合中的所有和外界的连边都是朝外的
通过期望的线性性可以做到 \(2^n\) 级别求答案
考虑将复杂度降为 \(m\) 有关
不妨枚举 \(m\) 条边的定向方式，那么对于一个集合，原来的贡献是 \(2^{x(n-x)}\)，每多一条固定的边，变化 \(2p\)
那么发现这个表达式中目前只与 \(x\)，即连通块大小有关系了
那么我们统计出每种大小的块的贡献，即定向以后形成若干连通块，对这些连通块做背包即可，这样复杂度是 \(2^mn^2\)
考虑不管边集怎样定向，最终形成的连通块的样子都是一样的，而且联通块的点数最多为 \(m+1\)，那么转而枚举每个连通块的情形，即可做到 \(2^{m+1}m\) 的复杂度了
欧拉路
欧拉路指经过图中每条边恰好一次的路径
欧拉回路还要求是一条回路，充要条件是所有点的度数为偶数
欧拉路径还可以有两个点为奇数，分别作为起点和终点
还有一个小性质：一个欧拉图是若干个环的并，且每条边被奇数个环包含
如果要求出图中的欧拉路径，只需要从起点开始 \(dfs\)，最后一定会在中结束
首先需要明确，为了保证正确性，一定一定要回溯时再入栈！！！
因为栈这个玩意儿有拼接功能，以这张图为例：
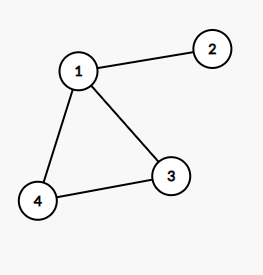
发现为了走最小的，会先到 \(2\) 号点，回溯，然后走一个圈，回到 \(1\) 号点，这样的顺序是 \(12341\)，这是不合法的
显然发现正确的走法是 \(13412\)
那么如果使用栈，会自然而然的记录成 \(21431\)，然后倒序输出即可
另一个坑点是每次 \(dfs\) 后要更新邻接表的 \(hd\) 值，比如构造出这样的图：
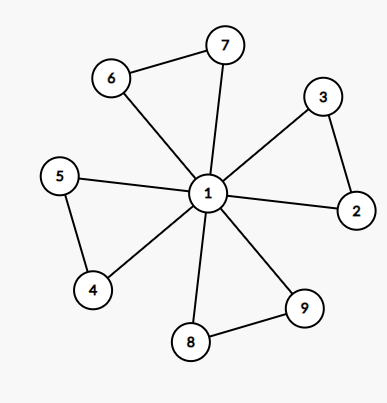
每次遍历完一个小图都会回到 \(1\) 号点，然后继续从头开始遍历邻接表，被卡成 \(n^2\)
一般我喜欢这样写：
for(int i=hd[u];i;i=edge[i].nxt){
int v=edge[i].to;
hd[u]=i;
dfs(v);
i=hd[u];
}
一般欧拉路径的题会藏得比较深，对于“每件物品只能使用恰好一次”等字眼要保持充分的警惕
首先把图中的连通块们都找出来，然后进行连接，首先如果连通块内部奇数点数量多，那么先两两匹配消掉，但是需要和别的相连，那么如果有奇数点直接连，然而如果一个没有则需要额外弄一个
遍历所有的道路，这样我们想到欧拉回路
但是原图上会产生奇数度点，根据贪心的策略，可以直接向下一个点连边，因为沿着多条这样的边走过去相当于走出任何情况
为了让图连通，还需要求一遍最小生成树，同样根据 \(kruscal\) 的理论，只在相邻的异色连通块间连边即可
AT3968 [AGC025E] Walking on a Tree
考虑如果已知可以都跑完该怎样构造方案，可以对两端点连边然后跑欧拉路即导出一种跑完所有路径的方案
如果建完图发现有点是奇数，那么可以类似于上一题一样直接将父子连边，这样可以考虑到所有情况
对于一张完全无向图，如果不连通，可行的办法是将所有奇数点连在超级点上跑一遍，可以保证此时所有点的度数 \(\le1\)
这启发我们在看到 \(\le1\) 的字眼时思考欧拉路径
对于混合图的求法，放到网络流里
欧拉图的计数
考虑欧拉图的关键性质是所有点的度数为偶数
那么考虑怎样计算偶图的个数
一种思考方式是由于任意连边后所有奇数度点再加一条边后就会变得合法，因此选出一个点后剩余点是可以随意连边的
而统计则为总偶图-不连通图偶图，这类容斥只需要枚举一个连通的，然后强行分开即可
注意这种拿出一个特殊点作为补偿点的思路在欧拉图中很常见！！
BEST 定理
一个有向图的欧拉回路个数为：
其中 \(w\) 为以某个点为根的内向生成树个数，\(out\) 为出度
注意这样计算下的个数是在去重循环同构的情况下的
那么需要手动乘上第一个点的度数 \(d\)
由于是无向图，只需要知道每个点的出度即可
考虑基环树上其实树边的定向方案是固定的，必须为 \(\frac{x}{2}\)，而环上只需要枚举出任意一条边的正方向个数，所有的点便都可以确定了
然后基环树上树形态计数也是非常简单的
