noip模拟31
\(\color{white}{\mathbb{峭壁通天，横崖无岸，惊无识之马，断无疆之虹，名之以：悬崖}}\)
一看完题就暴肝 \(t1\)，胡了两个贪心，实现了一个，发现都是错的，然后奖金两个小时还处于一分没有的状态
慌张之中赶紧打后两题暴力，\(t3\) 打了树形 \(dp\) 外加口胡部分分做法，期望70，然后十分钟又胡了一个 \(t2\) 的自认为的假贪心，然后又写了 \(t1\) \(n^3\) 的貌似正确的贪心
一度以为要暴零了，\(t2\) 生死未卜，\(t3\) 样例过水，也没对拍
考完发现好像都不高……
%%%两位巨佬场切 \(t2\)
A. Game
考场上想到一种看上去非常正确但其实无可救药的贪心方法：
随便生成一种答案最小的方案，然后枚举每个位置，试图和后面更大的交换
然而可能存在一种情况是本来和后面的大数交换不了，但是通过若干媒介实现了交换……
于是一个半小时只得到用来对拍的程序的20分的好成绩～
然后打完后两题暴力有回来看这题，又胡出了一个复杂度略高但肯定正确的做法，后来发现是正解的待优化版(强烈谴责出题人没给\(n^3\)的部分分)
首先算出最优答案，考虑每个位置，从大到小试图填未选的数，填入后计算答案若等于最优答案则可以选择
发现如果一个一个试太浪费了，可以尝试寻找单调性，采用二分的思想
写出来式子：\(presum+(b[i]>a[i])+sufsum\)
当前两项相同时，最后的值是满足单调的
由于随着 \(b[i]\) 的取值不同，中间的会不同，所以中间可能产生断层
画一个图图～
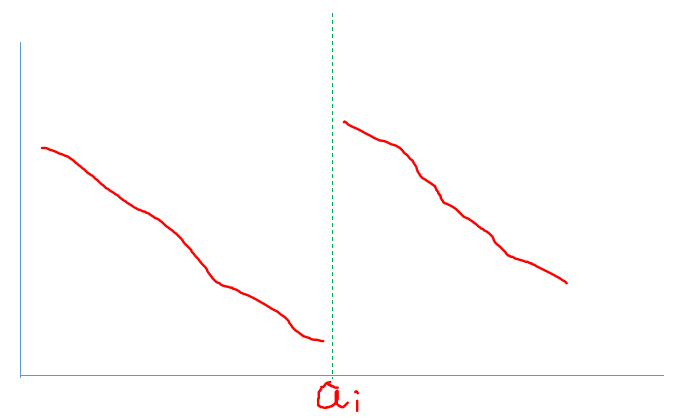
那么发现需要二分两次
首先尽量选大的，所以先二分右面，如果不行再来左边
然后就是怎样快速计算出一些 \(a、b\) 产生的贡献了
题解用了一棵玄妙的线段树
开一个权值线段树
每个节点记录区间内尚未抵消的 \(a\) 和 \(b\) 的数量
左右子树合并时每一个右子树的 \(b\) 都可以匹配左子树的一个 \(a\)，所以产生的贡献是两者个数的 \(min\)
然后发现二分的时候还需要一个东西维护当前剩下的 \(b\) 的集合，那么再开一棵权值线段树维护即可
总复杂度为 \(nlog^2n\)
代码实现
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
const int MAX=1e5;
int n,a[maxn],ans1[maxn],ans,pos[maxn],b[maxn];
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
struct Seg{
int l,r,sum,suma,sumb;
}t[maxn*4];
void build(int p,int l,int r){
t[p].l=l;
t[p].r=r;
if(l==r){
pos[l]=p;
return ;
}
int mid=l+r>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
return ;
}
void update(int p){
int sump=min(t[p<<1].suma,t[p<<1|1].sumb);
t[p].sum=t[p<<1].sum+t[p<<1|1].sum+sump;
t[p].suma=t[p<<1].suma+t[p<<1|1].suma-sump;
t[p].sumb=t[p<<1].sumb+t[p<<1|1].sumb-sump;
return ;
}
void add(int pp,int sum1,int sum2){
int p=pos[pp];
t[p].suma+=sum1;
t[p].sumb+=sum2;
while(p>>1){
p>>=1;
update(p);
}
return ;
}
namespace p1{
int pos[maxn];
struct Seg{
int l,r,num;
}t[maxn*4];
void build(int p,int l,int r){
t[p].l=l;
t[p].r=r;
if(l==r){
pos[l]=p;
return ;
}
int mid=l+r>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
return ;
}
void update(int p){
t[p].num=t[p<<1].num+t[p<<1|1].num;
return ;
}
void add(int pp,int w){
int p=pos[pp];
// cout<<p<<endl;
t[p].num+=w;
while(p>>1){
p>>=1;
t[p].num+=w;
// cout<<t[p].num<<" ";
}
return ;
}
int k_th(int p,int k){
if(t[p].l==t[p].r)return t[p].l;
int mid=t[p].l+t[p].r>>1;
if(t[p<<1].num>=k)return k_th(p<<1,k);
return k_th(p<<1|1,k-t[p<<1].num);
}
int pre(int p,int pos){
if(t[p].l==t[p].r)return t[p].num;
int mid=t[p].l+t[p].r>>1;
if(pos<=mid)return pre(p<<1,pos);
return t[p<<1].num+pre(p<<1|1,pos);
}
}
int main(){
n=read();
build(1,1,MAX);
p1::build(1,1,MAX);
for(int i=1;i<=n;i++)a[i]=read(),add(a[i],1,0);
for(int i=1;i<=n;i++)b[i]=read(),add(b[i],0,1),p1::add(b[i],1);
ans=t[1].sum;
int sum=0;
// cout<<ans<<endl;
for(int i=1;i<=n;i++){
add(a[i],-1,0);
// if(i==2){
// cout<<"hhh "<<p1::k_th(1,3)<<endl;
// }
int num=p1::pre(1,a[i]);
int l=num+1,r=n-i+1;
// cout<<l<<" "<<r<<endl;
while(l<r){
int mid=l+r+1>>1;
// if(i==2)cout<<mid<<" ";
int val=p1::k_th(1,mid);
add(val,0,-1);
// if(i==2)cout<<"ppp "<<mid<<" "<<t[1].sum<<endl;
if((t[1].sum+1+sum)==ans)l=mid;
else r=mid-1;
add(val,0,1);
}
// cout<<l<<endl;
int val=p1::k_th(1,l);
add(val,0,-1);
if((t[1].sum+(val>a[i])+sum)==ans&&l<=n-i+1){
ans1[i]=p1::k_th(1,l);
p1::add(ans1[i],-1);
sum++;
}
else{
add(val,0,1);
int l=1,r=num;
while(l<r){
int mid=l+r+1>>1;
int val1=p1::k_th(1,mid);
add(val1,0,-1);
if((t[1].sum+sum)==ans)l=mid;
else r=mid-1;
add(val1,0,1);
}
ans1[i]=p1::k_th(1,l);
add(ans1[i],0,-1);
p1::add(ans1[i],-1);
}
}
for(int i=1;i<=n;i++)cout<<ans1[i]<<" ";
return 0;
}
B. Time
又是一个玄妙的贪心
每次取最小值贪心地放在序列左边或者右边
这个可以先拍好序，数状数组维护移动产生的位置加减
当有值相同时出 \(bug\)，那么排序时以位置作为第二关键字，对于一个值，每次选取这个值所在区间左端点和右端点的数计算即可
代码实现
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int n,c[maxn],last[maxn];
long long ans;
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
struct P{
int val,id;
bool flag;
}a[maxn];
bool cmp(P a,P b){
return a.val!=b.val?a.val<b.val:a.id<b.id;
}
void add(int x,int op){
x++;
for(;x<=n+1;x+=x&-x)c[x]+=op;
return ;
}
int ask(int x){
x++;
int ans=0;
for(;x;x-=x&-x)ans+=c[x];
return ans;
}
int main(){
n=read();
// cout<<n<<endl;
for(int i=1;i<=n;i++){
a[i].val=read();
a[i].id=i;
}
// cout<<n<<endl;
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++){
if(a[i].val!=a[i+1].val)last[a[i].val]=i;
}
int l=0,r=0;
for(int i=1;i<=n;i++){
if(a[i].flag)continue;
if(i==last[a[i].val]){
int pos=a[i].id+ask(a[i].id);
/// cout<<"hhh "<<pos<<endl;
if(pos-l<(n+1-r)-pos){
l++;
ans+=pos-l;
add(1,1);
add(a[i].id+1,-1);
}
else{
ans+=(n-r)-pos;
r++;
add(a[i].id+1,-1);
}
}
else{
int pos1=a[i].id+ask(a[i].id);
int pos2=a[last[a[i].val]].id+ask(a[last[a[i].val]].id);
int dis1=min(pos1-l,n+1-r-pos1);
int dis2=min(pos2-l,n+1-r-pos2);
if(dis1<dis2){
if(pos1-l<=(n+1-r)-pos1){
l++;
ans+=pos1-l;
add(1,1);
add(a[i].id+1,-1);
}
else{
ans+=(n-r)-pos1;
r++;
add(a[i].id+1,-1);
}
}
else{
if(pos2-l<(n+1-r)-pos2){
l++;
ans+=pos2-l;
add(1,1);
add(a[last[a[i].val]].id+1,-1);
}
else{
ans+=(n-r)-pos2;
r++;
add(a[last[a[i].val]].id+1,-1);
}
a[last[a[i].val]].flag=true;
last[a[i].val]--;
i--;
}
}
// cout<<ans<<endl;
}
cout<<ans;
return 0;
}
C. Cover
首先有一个很明显的树形 \(dp\)，设 \(f[i][j]\) 表示以 \(i\) 为根的子树选取 \(j\) 层的最大值
转移：\(f[i][j]=max(\sum f[v][j],\sum f[v][j-1]+a[i])\)
那么发现如果树被构造地很长，转移很费时间
那么可以采用类似启发式合并的思想，先将 \(f[i]\) 继承于他最深的子树，然后转移
数组的继承不太好实现，可以使用堆 (堆的 swap 是 O(1)) 的
发现当前的 \(a\) 值产生贡献当 \(a[i]>f[i][j]-f[i][j-1]\)，发现出现了差分，可以再维护一个 \(g[i][j]=f[i][j]-f[i][j-1]\)，然后 \(g\) 是单调的，可以把这一堆东西放进堆继续维护
代码实现
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e5+5;
int n,m;
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
struct S{
int l,r,val,len;
}a[maxn];
bool cmp(S a,S b){
return a.len<b.len;
}
namespace p1{
int ans,mxdep[maxn],son;
long long g[maxn];
struct Edge{
int nxt,to;
}edge[maxn];
int hd[maxn],cnt;
void add(int u,int v){
// cout<<u<<" "<<v<<endl;
edge[++cnt].nxt=hd[u];
edge[cnt].to=v;
hd[u]=cnt;
return ;
}
priority_queue<long long>f[maxn];
void dfs(int u){
mxdep[u]=1;
int son=0;
for(int i=hd[u];i;i=edge[i].nxt){
int v=edge[i].to;
dfs(v);
mxdep[u]=max(mxdep[u],mxdep[v]+1);
if(mxdep[v]>mxdep[son])son=v;
}
swap(f[u],f[son]);
for(int i=hd[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v!=son){
int s=f[v].size();
for(int j=1;j<=s;j++)g[j]=f[u].top(),f[u].pop();
for(int j=1;j<=s;j++)g[j]+=f[v].top(),f[v].pop();
for(int j=1;j<=s;j++)f[u].push(g[j]);
}
}
f[u].push(a[u].val);
return ;
}
void start(){
sort(a+1,a+m+1,cmp);
a[m+1].l=1,a[m+1].r=n;
for(int i=1;i<=m;i++){
for(int j=i+1;j<=m+1;j++){
if(a[i].l>=a[j].l&&a[i].r<=a[j].r){
add(j,i);
break;
}
}
}
dfs(m+1);
int s=f[m+1].size();
for(int i=1;i<=s;i++)g[i]=f[m+1].top(),f[m+1].pop();
for(int i=1;i<=m;i++){
g[i]+=g[i-1];
printf("%lld ",g[i]);
}
return ;
}
}
signed main(){
n=read();
m=read();
for(int i=1;i<=m;i++){
a[i].l=read();
a[i].r=read()-1;
a[i].val=read();
a[i].len=a[i].r-a[i].l+1;
}
p1::start();
return 0;
}
\(\color{white}{\mathbb{宝剑锋从磨砺出,梅花香自苦寒来。}}\)
