noip模拟16
\(\color{white}{\mathbb{雨淅惊梦，黯然无光，颓然于角落，空对四角之天怅惘焉，名之以：谷底}}\)
考场
再次对难度估计错误，以为 \(t1\) 是二分，而且非常显然嘛，觉得这场考试估计比较简单，那么 \(t2\)、\(t3\) 必须再有一道做得差不多才能有一个不错的名次，于是半个小时是就把 \(t1\) 写完了，根本没对拍没查错。
然后花了两个小时看 \(t2\)，也没有胡出一个靠谱的方法。
\(t3\) 本来大了一个非常漂亮的暴力，又胡了一个觉得正确其实很不正确的单调栈做法，以为暴力只能过20%的数据，于是判了一下，没想到数据有锅没给够部分分，而且居然能过随机数据，居然还有一个水的点也能过，于是人均暴力50的题只拿了10分
（tips：一般随机数据下树的形态非常好，可以认为是 \(log\) 的期望）
于是又有一个非常非常难看的成绩……
\(rk1\) 130
\(cyh\) 巨佬 110 \(rk3\)
A. Star Way To Heaven
考场上一眼看到最小值最大，以为是二分裸题，再加上一个 \(k^2\) 建图 \(O（k）\) dfs一遍check，稳稳能过80分。结果……T成20
一开始以为有环，后来想了一晚上才想清楚
首先必须要开个vis数组记录走过的点不能再次经过，虽然是有向图也会被这种图卡到T
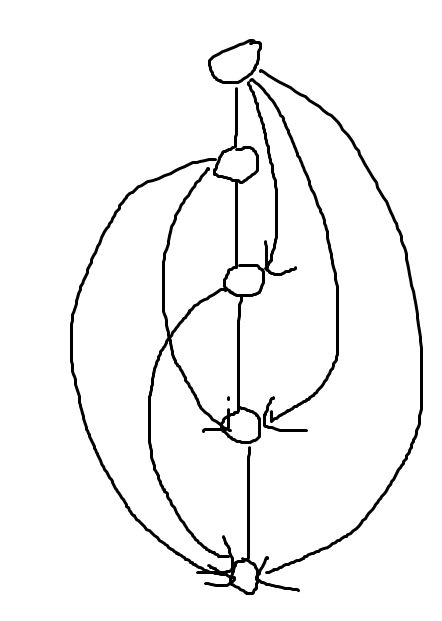
这题需要建双向边，因为会出现这样的阻拦地带：
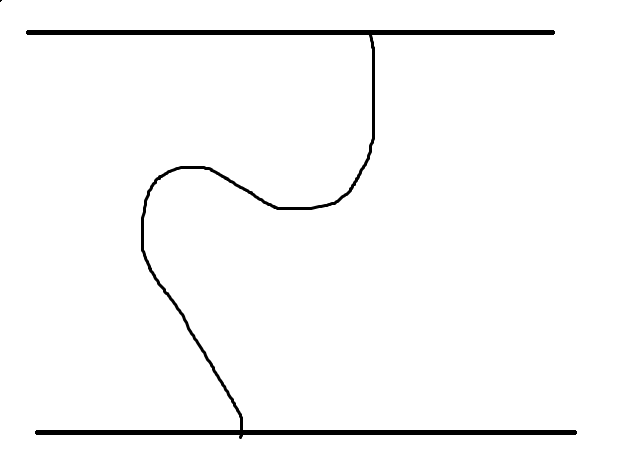
正解并不需要二分，直接最小生成树
将上边界看做起点，下边界看做终点，跑一遍最小生成树相当于找到了限制他往右走的一系列横贯上下的点，只要他能从这道墙走过去，那么一定可以走过剩下所有的墙（因为穿过一堵墙需要走最大值的地方，既然其他的墙没有贯通到下边界，那么一定证明中间有一个很大的空隙导致这些点一直没有更新到树里，从这个缝隙可以轻易穿过这堵墙），那么穿过这些点距离最远的点对之间的缝隙可以取到最大值
可以算是最小生成树的经典妙用，最小生成树经常可以用来维护路径上最小值问题，比如这道题比较类似
关于实现，因为是完全图，需要用 \(prim\)
代码实现
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int n,m,k;
double x[maxn],y[maxn],dis[maxn],ans;
bool vis[maxn];
int main(){
dis[0]=1000000000;
cin>>n>>m>>k;
for(int i=1;i<=k;i++){
cin>>x[i]>>y[i];
dis[i]=y[i];
}
dis[k+1]=m;
while(1){
int u=0;
for(int i=1;i<=k+1;i++){
if((!vis[i])&&dis[i]<dis[u])u=i;
}
ans=max(ans,dis[u]);
vis[u]=true;
if(u==k+1)break;
for(int i=1;i<=k;i++){
dis[i]=min(dis[i],sqrt((x[i]-x[u])*(x[i]-x[u])+(y[i]-y[u])*(y[i]-y[u])));
}
dis[k+1]=min(dis[k+1],m-y[u]);
}
printf("%.8lf",ans/2);
return 0;
}
B. God Knows
这道题算法极不明显，考场上在这道题上花费了很多时间，先后想到建图、网络流、dp 等一系列做法，但是最后 dp 状态没有设计对
考场上设计的状态是 \(f[i][0/1]\) 表示这个点及以前的点都被割掉，这个点选不选的最小花费，但是发现状态有杂糅，非常不好区分
正解是这样的 \(f[i]\) 表示选这个点且这个点以前的点都被割掉，这样设计状态不重不漏，可以很方便地从 \(f[j]\) 转移
然后思考转移条件，如果 \(j\) 是 \(i\) 之前最后一个选的点，那么要保证 \([j+1,i-1]\) 的所有点都没割过，那么要么 \(p_k>p_i\)，要么 \(p_k<p_j\)，这样就设计出了 \(n ^ 2\) 的dp
可以发现在 \(i\) 固定的情况下，\(j\) 的候选集合的 \(p\) 值是单调递减的，可以画个图理解一下
于是这是一个单调栈问题，然而棘手的问题是对于每个 i 来说 \(p_j \le p_i\) 这个条件都不相同，单调栈的形态是不一样的
那么现在有两个约束条件：\(j<i\) 和 \(p_j<p_i\)
那么想到第一个条件好满足，那么可以以第二个条件为下标构建单调栈，那么 \(p_i\) 左边的所有值都是可选的。
首先可以发现转置以后还是单调递减的（注意这里的翻转，如果原来的坐标是（i,p[i]），那么翻转后坐标是\((p[i],MAX-i)\)，这样画出图来以后可以发现还是递减的）
这样整个横坐标表示的是 \(p\) 数组，坐标上面对应的值表示对应的 \(i\) 的值，用以满足第一个条件，每个位置拥有一个值表示 \(f\) 数组的 dp 值
对于这个问题需要用线段树来维护
维护的时候维护两个变量，\(lmn\) 表示左半个区间里面大于右半个区间最大值的最小的高度对应的 \(f\) 值，\(mx\) 表示整个区间里最大的高度
首先写一个 \(calc\) 函数，用来查询区间内大于标准值的单调栈的最小元素的 f 值
查询的时候要先计算右区间，将标准值设为右区间的最大值，再进入左区间统计答案
代码实现
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
const int inf=0x3f3f3f3f;
int n,p[maxn],now,ans,x;
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
struct Seg{
int l,r,lmn,mx,f;
}t[maxn*4];
void build(int p,int l,int r){
t[p].l=l;
t[p].r=r;
t[p].lmn=inf;
if(l==r)return ;
int mid=l+r>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
return ;
}
int calc(int p,int limit){
if(t[p].l==t[p].r){
if(t[p].mx>limit)return t[p].f;
return inf;
}
if(t[p<<1|1].mx>=limit)return min(t[p].lmn,calc(p<<1|1,limit));
return calc(p<<1,limit);
}
void insert(int p,int pos,int height,int val){
if(t[p].l==t[p].r&&t[p].l==pos){
t[p].mx=height;
t[p].f=val;
return ;
}
int mid=t[p].l+t[p].r>>1;
if(pos<=mid)insert(p<<1,pos,height,val);
else insert(p<<1|1,pos,height,val);
t[p].lmn=calc(p<<1,t[p<<1|1].mx);
t[p].mx=max(t[p<<1].mx,t[p<<1|1].mx);
return ;
}
void ask(int p,int pos){
if(t[p].r<=pos){
ans=min(ans,calc(p,now));
now=max(now,t[p].mx);
return ;
}
int mid=t[p].l+t[p].r>>1;
if(pos>mid)ask(p<<1|1,pos);
ask(p<<1,pos);
return ;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
p[i]=read();
}
build(1,1,n);
for(int i=1;i<=n;i++){
x=read();
now=0,ans=inf;
ask(1,p[i]);
insert(1,p[i],i,(ans!=inf)?ans+x:x);
}
ans=inf;
now=0;
ask(1,n);
cout<<ans;
return 0;
}
C. Lost My Music
先把柿子化一下：
如果把每个点坐标看做 \((dis[i],c[i])\)，那么要求的式子相当于两点连线的斜率
这个可以维护下凸壳来做
将每个点的所有祖先用单调栈维护出下凸壳，但是如果暴力弹栈暴力回溯会TLE，那么可以考虑采用倍增弹栈，每个节点 \(f[i][j]\) 表示凸包上 \(2^j\) 的祖先是谁，每次如果有弹栈操作不是真的弹掉，而是把当前节点的父亲认作凸包上第一个满足条件的节点即可
代码实现
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
const int maxm=2e6+5;
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
int n,c[maxn],dep[maxn],f[maxn][25],fa[maxn],hd[maxn],cnt,x;
struct Edge{
int nxt,to;
}edge[maxm];
void add(int u,int v){
edge[++cnt].nxt=hd[u];
edge[cnt].to=v;
hd[u]=cnt;
return ;
}
bool check(int k,int j,int i){
return 1ll*(c[i]-c[j])*(dep[j]-dep[k])<=1ll*(c[j]-c[k])*(dep[i]-dep[j]);
}
void dfs(int u){
dep[u]=dep[fa[u]]+1;
int p=fa[u];
for(int i=20;i>=0;i--){
if(f[p][i]<=1)continue;
int t=f[p][i];
if(check(f[t][0],t,u))p=t;
}
if(p!=1){
if(check(f[p][0],p,u))p=f[p][0];
}
f[u][0]=p;
// cout<<p<<endl;
for(int i=1;i<=20;i++){
f[u][i]=f[f[u][i-1]][i-1];
}
for(int i=hd[u];i;i=edge[i].nxt){
int v=edge[i].to;
dfs(v);
}
return ;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
c[i]=read();
}
for(int i=2;i<=n;i++){
fa[i]=read();
add(fa[i],i);
}
dfs(1);
for(int i=2;i<=n;i++){
// cout<<i<<" "<<f[i][0]<<endl;
printf("%.10lf\n",(double)(c[f[i][0]]-c[i])/(double)(dep[i]-dep[f[i][0]]));
}
return 0;
}
\(\color{white}{\mathbb{会当凌绝顶，一览众山小}}\)
