最短路
最短路算法
Bellman-Ford
没想到这个算法还真的有用
它其实就是不断地进行松弛,一次松弛是用每一条边更新其出点的距离
那么一般情况下进行 \(n\) 次就一定可以完成所有更新
否则就说明出现了负环,即如果设 \(f[i][j]\) 表示第 \(i\) 轮更新第 \(j\) 个点的距离,那么 \(\exists v,f[n-1][v]>f[n][v]\) 时产生了负环
可以发现其本质上是在把负环的求解 \(dp\) 化,这样的工作 \(spfa\) 是不能胜任的
考虑原图上的一个环会对答案产生什么影响,可以统计其环上 \(x\) 的系数,写成 \(kx+b\) 的形式
考虑在负环条件的约束下,当 \(k\) 相等时,一定是 \(b\) 越小约束性越强
因此可以对每一个 \(k\) 跑出最短路
即设 \(f[t][u][k]\) 表示第 \(t\) 轮第 \(u\) 个点经过 \(k\) 个 \(x\) 的最短路
此时对于每一个点 \(u\),为了不在这个点上产生负环,那么需要保证 \(min_i f[n-1][u][i]+ix\le min_j f[n][u][j]+jx\)
那么即 \(\forall i,\exists j, f[n-1][u][i]+ix\le f[n][u][j]+jx\)
那么就是对这个不等式先求解,然后求出并集,再对所有 \(i\) 的答案求交集
同时每个点 \(i\) 对能到达的点更新取值范围
直接应用
这道题居然想到了状态:\(f[i][j]\) 表示节点 \(i\) 经过距离比最短路多 \(j\) 的方案数,由于 \(k\) 特别小,所以第二维可以装下。转移也比较容易
关于这题零环的判断以及多次绕正环的处理比较麻烦,于是采用新科技——倒叙dfs遍历
因为从终点开始遍历可以减去很多超过 \(k\) 的枝,对于零环,每次遍历都用 \(bool\) 打标记,如果一个点在相同深度经过了两次,说明有零环直接退就可以了
首先看清题——修改是暂时的,只对当前询问有效!!!
可以分类讨论:
- 不在最短路上,变大了:答案不变
- 不在最短路上,变小了:答案可能变成 \(dis(1,u)+dis(v,n)+val\)
- 在最短路上,变小了:答案可能变成 \(dis(1,n)-edge[i].val+val\)
- 在最短路上,变大了:这时是最棘手的情况,可能最短路变成了其他路径,然而并不一定是原图上的次短路,因为次短路可能也用到了这段路径
于是引入新科技——线段树来求解
首先预处理出原图的一条最短路径,并记录上面所有的边、点
线段树维护不经过路径上区间 \([l,r]\) 的点的最短路长度
至于维护,需要预处理另外一个东西:
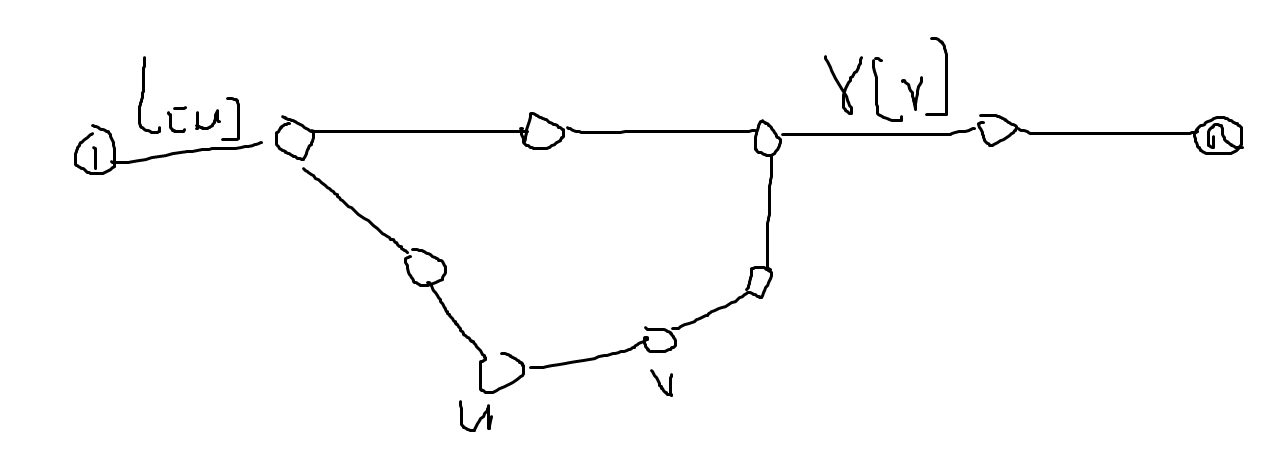
像这张图一样,\(l[u]\) 表示从1到 \(u\) 这个点经过最短路上最后一条边是哪一个,\(r[v]\) 同理
这样对于每条边,更新其端点限制的一段区间即可,即 \(l[u]+1,r[v]-1\)
发现最短路不再仅和到达的时间有关了,还和保护它的所有点什么时候走到有关
于是设 \(arrive[i]\) 表示走到这点的时间最短是多少(相当于原来的 \(dis\))
\(into[i]\) 表示这个点所有保护节点最晚被炸的点时间是多少
那么 \(dis[i]=max(arrive[i],into[i])\)
按原来的写法转移即可
至于为啥不开 long long 就能水过去俺也不知道
二维最短路
其实也就见过一个题还起个这么大的名字hhh
设 \(dis[x][y]\) 表示从 \(1\) 走到 \(x\) 以及 \(y\) 走到 \(1\) 的总代价
其中第二部分跑反向边变成 \(1\) 走到 \(y\)
那么每次分别尝试更新 \(x\) 的出边和 \(y\) 的出边,并且用 \(bitset\) 保存最优状态下走过了哪些点
最短路树
对于一个固定起点,只保留其到各点最短路上边而形成的树形图即为最短路树。
性质:每个点到根节点的距离即是其最短路
构建:每次最短路更新时记录每个节点最后一次由哪条边更新的,那么这条边是这个点的父亲边
最短路 \(DAG\)
最短路 \(DAG\) 就是对于所有保留了不会破坏从 \(s\) 出发的最短路的边形成的有向图
然后便可以在上面使用拓扑排序等来处理
答案为同时保留两人最短路 \(DAG\) 上的公共边形成的有向图的最长链
以每个标签为起点 \(s\) 跑最短路,然后处理这个标签的所有知识点的答案
可以发现对与一个点 \(v\),设 \(w\) 为 \(s\) 到 \(v\) 的距离,\(i\) 到 \(v\) 的答案是 \(w\) 或 \(w-1\),而这个取决于最短路 \(DAG\) 上的到达关系,那么跑出来以后看是前驱还是后继即可
首先对于每个起点建出 \(DAG\),然后拓扑排序即可,只需要 \(f[v]+=f[u]\)
然后每条边是 \(f_u* g_v\),正确性不难理解
下面的算法涉及最短路的本质
来看一下最短路的本质式:
\({\color{Violet} {\LARGE f[v]=f[u]+val_{(u,v)} } }\)
以及跑完以后满足的性质:
\({\color{Violet} {\LARGE f[v]\le f[u]+val_{(u,v)} } }\)
负环和差分约束
既然跑完满足那个性质,那么对于不等式组 \(dis_v-dis_u\le val\) 都是成立的
因此可以通过跑最短路来判断不等式组成立并给出合法解
首先可以把所有提供的信息以及询问转化为每两个砝码差值可能的取值范围 \([l,r]\)
那么对于上界跑最短路,下界跑最长路,\(floyd\) 一下即可算出
Johnson 全源最短路
最传统的方法碰上稠密图直接 \(O(n^3)\) Floyd
还有一种每个点跑一边 dij,复杂度 \(O(nmlog(n))\)
但是 dij 的天然缺陷是不能处理负边权
于是看上面,发现了性质式长得挺好
有一个值非负:\(f[u]+val_{(u,v)}-f[v]\),要是把这个值当成新权值弄进去就好了
为了处理出一个 f,可以建一个虚拟零号点,向每个点连一条边跑一遍最短路
这样以后最终的最短路也发生了相应的改变
先给结论: \(dis(u,v)=dis'(u,v)+f_v-f_u\)
简单证明(抄袭)一下:
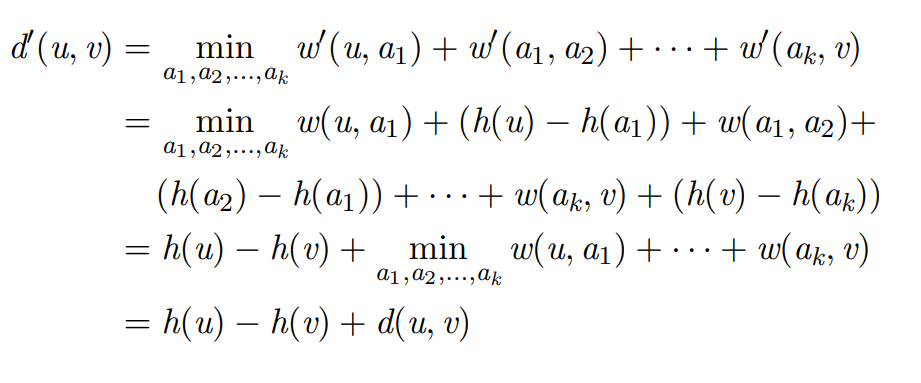
找到一一对应关系以后便可以变回去了
同余最短路
从这道经典例题说起:
首先可以钦定一个最小的数作为模数(这道题即为 x),然后努力用其他数拼出一些层,则一直加 x 即可算出所有可达层
由于模x没有影响,设 \(f(i)\) 表示用其他数可以拼出的模 x 等于 i 的最小层数
转移:\(f((i+y)\%x)=f(i)+y\)
咦?这和转移的本质式很像诶~
于是转到图上来,根据对应关系建边 \((i,i+y)\)
之后跑一遍最短路,那么结果便是所求
再有就是加强版本: P2371 [国家集训队]墨墨的等式
一些trick
二进制拆分
对于这类一些点之间的最短路而且不需要辨别点点区别,可以采用多个起点同时跑最短路的思路,把一些点一起丢进堆里,最后一起统计距离
那哪些点做起点呢?
由于关键点非起点即终点,可以采用二进制拆分的思想,对于每一位,分别让 0和1 的点当起点和终点,由于没有两个点编号完全相同,这样可以做到不重不漏
貌似这道题的最优秀的解法并不是二进制拆分,比如这道题时间就被卡了
有两种更优秀的做法:
法一:直接多源最短路,标记每个点转移点的源点,最后枚举每一条边,如果两端点颜色不同,更新这两点的答案
法二:直接求多源次短路,由于最短路一定是自己,那么次短路是满足条件的
首先最小环可以转化成这样的问题:从1号点跑最短路,对于一个包含节点 u、v 的环,长度为 \(dis(1,u)+dis(1,v)+dis(u,v)\)
发现式子里又出现了经典模型,二进制处理即可
最小环问题
对于有向图最小环,可以直接 \(floyd\),无向图上当然也可以像上面那样二进制分组,这里介绍一种更简便的 \(floyd\) 方法
考虑 \(floyd\) 的每一轮,相当于是求出了任意两点间经过 \(1\sim i\) 的最短路
那么可以发现刚进入某一轮的时候,\(i\) 一定还不在 \(u,v\) 的最短路上,那么此时更好可以统计出经过 \(i\) 点的最小环了
for(i = 1; i <= V; ++i){
for(u = 1; u < i - 1; ++u)
for(v = u + 1; v < i; ++v)
down(w, G[i][u] + d[u][v] + G[v][i]);
for(u = 1; u <= V; ++u)
for(v = 1; v <= V; ++v)
down(d[u][v], d[u][i] + d[i][v]);
}
边权相等
如果每个节点的出边都是一个固定的权值,那么此时可以直接把 \(dis_u+a_u\) 扔进堆里,此时每个点只会被放进去一次,获得很优的复杂度
这道题就是一个经典应用,这个 \(trick\) 提供给点分树以正确的复杂度,否则如果被压进堆里可能会更新多次


 浙公网安备 33010602011771号
浙公网安备 33010602011771号