树形dp
树形背包
树形背包类问题的模型一般是选择不超过 \(m\) 个点求最值，通常会出现诸如选儿子必须先选父亲的条件，因此，对于每一个节点的子树而言，每一个儿子相当于分组背包的一个组，而像下图不同颜色标注的选取部分相当于每组中可选的物品。
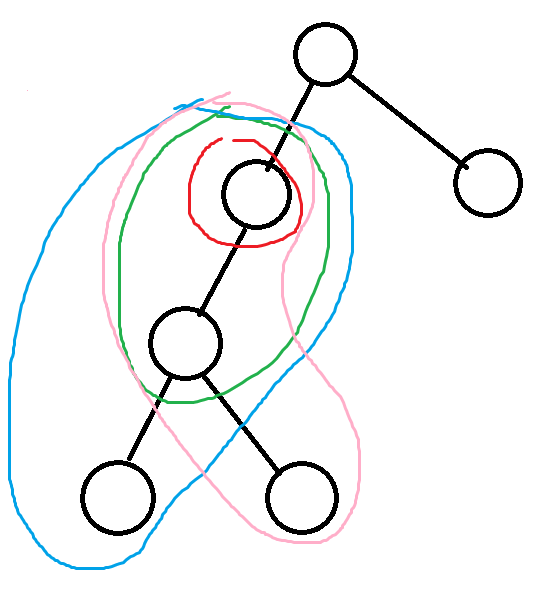
从一道例题说起：
很明显，选择的课程个数相当于物品，而先修的规则满足树形背包的要求。
按照一般套路，设 \(f[i][j]\) 表示以 \(i\) 为根的子树中选修 \(j\) 门课获得的最大学分是多少
转移类似于分组背包，枚举儿子 \(v\) 相当于枚举组，第二维倒序枚举容量，第三位枚举物品，则 \(f[u][j]=max\{f[u][j-k]+f[v][k]\}\)
好的，目前时间复杂度为 \(O(n^3)\)
再来考虑优化：
观察代码，发现枚举背包容量的时候每次都要枚举到 \(m\)，这其实非常浪费的，因为有可能当前子树很小，则容许的背包容量也很小。
于是可以只枚举到 \(siz[u]\) 即可
关于时间复杂度：总之这样是 \(O(n^2)\) 的，至于为什么——简单理解一下因为每个点对都只在LCA 处计算一次
对于背包容量上限较大的题，更严格的复杂度是 \(O(nm)\)
这几道题很类似且较为简单：
P1272 重建道路
P1270 “访问”美术馆
CF815C Karen and Supermarket
一年前曾经做过然而现在又不会了……
直接算点对肯定不好算，那么考虑每条边权对答案的贡献
那么只要知道边两端黑白点个数分别是多少便可以
由于黑点总数已知，那么只需要记录黑点个数，便可以知道其他所有信息
设 \(f[i][j]\) 表示子树内共有 \(j\) 个黑点的总和，树形背包转移即可
下面就是难一点不会做的题了
首先，放置监听器数量的严格固定，相当于背包容量
这题有一个非常特殊的限制——“放置在节点 u 的监听设备并不监听 u 本身的通信”，于是对于一个点的状态并不只受当前点放不放的控制
另一个关键点是因为管辖半径为1，那么对于节点 u 来说，如果儿子没被监听，u也不监听，那么以后就没有机会了，所以对于 u 节点的子树，除 u 节点外其他节点必须已经被监听
于是设计状态： \(f[u][j][0/1][0/1]\)表示节点 u 的子树共使用 j 个监听器，u 节点是否放置， u 节点是否被监听，且此时其他点都被监听的方案数
由于涉及组合数学，可以考虑直接按照优化后的树形 dp 来写会更方便。
于是 4 种情况分别转移：
\(f[u][j+k][0][0]+=f[u][j][0][0]*f[v][k][0][1]\)
\(f[u][j+k][0][1]+=f[u][j][0][0]*f[v][k][1][1]+f[u][j][0][1]*(f[v][k][0][1]+f[v][k][1][1])\)
\(f[u][j+k][1][0]+=f[u][j][1][0]*(f[v][k][0][1]+f[v][k][0][0])\)
\(f[u][j+k][1][1]+=f[u][j][1][0]*(f[v][k][1][0]+f[v][k][1][1])+f[u][j][1][1]*(f[v][k][0][0]+f[v][k][0][1]+f[v][k][1][0]+f[v][k][1][1])\)
注意这道题 m 很小，而 \(size[u]\) 很大，需要取 \(min\)
和上道题比起来，数据范围友好了许多，但是有一个很难受的是价值的计算，为到最近伐木场的距离，这样以来一个节点的状态不再之和父亲、儿子有关，而是需要关联到很远的祖先
状态为：\(f[u][j][k][0/1]\)表示u节点最近的建场祖先是 j 节点，子树内共建场k个，u建没建的最小代价
由于这道题节点数量本身很小，可以直接枚举祖先
转移：
\(f[u][j][k][0]=min(min(f[v][j][k-x][0]+f[u][j][x][0])+val,f[u][j][k-1][1])\)
\(f[u][j][k][1]=min(f[v][u][k-x][0]+f[u][j][x][1])+val\)
\(val=sum[u]*(deep[j]-deep[u])\)
注意这里，相当于把 \(f[u][][][1]\) 向 \(f[u][][][0]\) 合并，方便下一层的转移
换根 \(dp\)
对于树的方向（即根的不同）对答案产生影响的 \(dp\)，往往可以通过换根 \(dp\) 来求出每个点为根的答案
换根的过程关键在于消除子树影响
对于最值问题的 \(dp\) 通常可以记录子树的最小值和次小值的方式来实现
对于加和之间减去，乘积问题可以处理逆元，比如 B. 树论
对于一些朴素的换根 \(dp\)，可以使用 up and down 的方式简单书写
比如树上最短路，可以直接向上取 \(min\)，向下取 \(min\) 即可，这种 \(min\) 和 \(max\) 都不会算重不会产生问题
树形 \(dp\) 的优化
树形 \(dp\) 的第二维常常与子树大小、深度有关，那么采用启发式合并的思路直接把重（长）儿子的信息继承过来复杂度就可以优化为 \(log\) 级别
可以发现在这种情境下树内的物品没有限制关系，是随意选的，那么可以发现第二维越大得到的新贡献就越小，因此 \(f\) 的差分数组是单调的
把差分放进堆里，利用堆 \(swap\) 的 \(O(1)\) 特性复杂度就变得正确了
具体见 这里
注意这道题并不能长剖，因为要求求出每个的值
对于一种特殊的 \(dp\)，其每个节点上的合法状态都是一些区间集合，并且叶节点区间个数为 \(1\)，这样的 \(dp\) 如果合并过程中保证每个节点的区间都是没有包含关系的话，复杂度也是 \(log\) 的
其他神奇的树形dp
上下分别维护
一些题中需要统计树上满足条件的路径数，并且路径具有一定的方向性
那么可以 \(dp\) 出一个点子树向上路径和向下路径分别的 \(dp\) 值，在当前节点进行拼接
神奇的 \(dp\) 题
首先发现作为起点是独特的，贡献为周围点权和，其他地方都需要减去父亲节点的权值
那么需要区分起点和终点，可以设 \(f[u][i]\) 表示以 \(u\) 为根的子树里从某个点为起点到点 \(u\) 的路径撒了 \(i\) 次的最大收获
\(g[u][i]\) 表示从 \(u\) 开始到从 \(u\) 到以 \(u\) 为根子树内一点作为终点的的路径撒了 \(i\) 次的最大收获
那么更新答案为 \(f[u][i]+g[v][m-i]\)，考虑更新：
初始化为 \(f[u][i]=sum[u]\)，\(g[u][i]=sum[u]-a[father]\)
实现的时候还有一个问题：由于一个是起点另一个是终点，更新答案是根据儿子的顺序来更新的，那么遍历的顺序是有影响的，还需要倒的扫一遍
这道题的巧妙之处更在于条件的转化
可以每种颜色分开考虑：一种颜色的贡献是 包含这种颜色至少1个点的路径条数
继续转化，一般情况“至少为1”这样的条件不好处理，可以利用补集思想用总路径条数减去没有出现这种颜色点的路径数
首先来看暴力算法：
因为固定颜色后是这种颜色的点不能经过，于是这种颜色的点将整棵树分割成若干个连通块，每个连通块中所有路径均满足条件，贡献 tot*(tot-1)/2 条路径
时间复杂度 \(O(n^2)\)
再来优化，首先可以将形式变为树形 \(dp\), 开一个二维数组放颜色，这样就改成了普通 dp 的样子
于是现在优化以后时间空间都过不去了
再来考虑，因为一个点只有一种颜色，所以除了这种颜色以外其他颜色的转移都是在浪费时间，于是只考虑当前颜色即可，解决了时间问题
因为子树的连续性以及分割，每种颜色没必要每个点开一个，开成全局记录即可，对于当前连通块的统计可以用子树总大小减去被截出去的部分，解决了空间问题
于是解决了这道题
首先要解决一个问题是怎样求一个子树的重心
一个比较方便的做法是一直走重儿子，直到其子树大小小于等于总点数一半
但是如果暴力跳会非常慢，可以考虑倍增，\(f[i][j]\) 表示节点 \(2^j\) 倍重儿子是谁
再考虑统计答案
从根节点出发，每次将一个节点作为根，其与一个儿子的连边作为答案统计边，然后分别求出以 \(u\) 为根的子树和以 \(v\) 为根的子树内重心并统计答案
有一个问题是当换根时父子关系转置，重儿子要重新更新，并且枚举到的 \(v\) 不能作为重儿子
当找到子树内倍增后的最后一个点后需要判断两个重心的情况，那么将其父亲、重儿子、自己都判断一下统计进答案
杂题
考虑两个人的移动方式是怎样的
一定是一个人往叶子上走，这个人等着传送，直到最后一次出发，这个人同时向剩下的那个子树中移动
那么设 \(f_u\) 表示到达 \(u\) 且子树外已经计算过的最优情况
转移方程为
\(d_m[u,v]\) 为主链上结点 u 到 结点 v （不包括结点 v） 往外伸出去的子树中最深的叶子的深度
观察发现有结论每次从 \(fa+1\) 转移过来的同时，只需要转移 \(d_m[u]\ge d[v]\) 的节点即可
进一步发现这类似于多步转移，那么只需要找到单调递减栈上最后一个点转移即可
于是就需要找到每个点上方第一个 \(d_m\) 大于它的点
当然可以二分栈之类的科技
一种神奇的方式是从下往上合并，然后子树之间暴力抵消更新，这样做完的复杂度正确！
考虑这个过程的本质，其实就是说从 \(s\) 的深度都 \(t\) 的深度，把所有深度的点的权值取 \(max\) 作为深度的权值，那么一定是对着深度尽量小的权值一直死，然后晋级到下一深度，以此类推，直到能走过路径上的最大值为止
于是相当于要动态地对深度维护单调栈
现在要做的就是单调栈的合并，可以发现启发式合并复杂度正确，为 \(O(nlogn)\)
