联赛测试2 3.25
A. Merchant
考场上很快看上去像是个二分，然而斜率有下降的造成错觉导致一直没有证出来，再加上没有及时 return 爆了 long long ，最后交上乱搞的版本分还变低了……
证明
对于所有 \(k_i\) 大于 0 的情况，很容易证明出是单调递增的
对于存在 \(k_i<0\) 的情况：若 t=0 的时刻值已经满足，则 0 为答案；否则，由于题目规定保证有解，则存在某个 t>0 满足条件，那么 \(\sum k_i\) 一定大于零，函数仍为单调递增的
而二分答案后贪心选取前m大且大于零的，直接sort 会TLE，可以使用 c++11 内置函数 \(nth\_element()\) 实现，这个函数会在 \(O\)（\(len\)） 时间内将数列中第 k 大的数放在第k 的位置上，且比k小的数在位置 k 左侧“乱序”排列，大的元素同理
代码实现
const int maxn=1e6+5;
ll y[maxn],d;
ll k[maxn],b[maxn],n,m,a[maxn],sum;
bool check(ll x){
for(int i=1;i<=n;i++){
y[i]=k[i]*x+b[i];
}
nth_element(y+1,y+n-m+1,y+n+1);
ll sum=0;
for(int i=n;i>=n-m+1;i--){
if(y[i]>0)sum+=y[i];
if(sum>=d)return true;
}
return false;
}
int main(){
n=read();
m=read();
d=read();
for(int i=1;i<=n;i++){
k[i]=read();
a[i]=b[i]=read();
}
sort(a+1,a+n+1);
for(int i=n;i>=n-m+1;i--){
if(a[i]<0)break;
sum+=a[i];
}
if(sum>=d){
cout<<0;
return 0;
}
ll l=0,r=1e9;
while(l<r){
ll mid=l+r>>1;
if(check(mid))r=mid;
else l=mid+1;
}
cout<<l;
return 0;
}
//数据比较水，下面这个样例有的题解过不了
/*
2 1 100
-100 105
1 1
*/
B. Equation
考场上曾经想到将每个变量用 \(x_1\) 表示出来，然而想着走到别的枝上在爬树回去，中间不知道哪里写挂了……
正解：
将每个变量表示出来后，得 \(X_u=a-X_1\), \(X_v=b-X_1\),再加上 \(X_u+X_v=S\) ,可以解出 \(X_1\) 。
然而每次X的表达式可以考虑通过树状数组维护的树上差分实现。由于值是一正一反相减得到的，那么深度为奇数的点的值之间有差分关系，而偶数点通过求父亲推倒即可
代码实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e6+5,maxm=1e6+5;
int n,q,cnt,hd[maxn],c[maxn],dep[maxn],fa[maxn],val[maxn],num[maxn],tot,size[maxn],op,x,y,u,v,w;
struct Edge{
int nxt,to;
}edge[maxm];
void add(int u,int v){
edge[++cnt].nxt=hd[u];
edge[cnt].to=v;
hd[u]=cnt;
return ;
}
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
void update(int x,int y){
for(;x<=n;x+=x&-x)c[x]+=y;
return ;
}
int sum(int x){
int ans=0;
for(;x;x-=x&-x)ans+=c[x];
return ans;
}
void dfs(int u,int deep){
dep[u]=deep;
num[u]=++tot;
size[u]=1;
for(int i=hd[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa[u])continue;
dfs(v,deep+1);
size[u]+=size[v];
if((deep+1)&1){
update(num[v],val[v]-val[u]);
update(num[v]+size[v],val[u]-val[v]);
}
}
return ;
}
int ask(int p){
if(dep[p]&1){
return sum(num[p]);
}
return val[p]-sum(num[fa[p]]);
}
signed main(){
// freopen("shuju.in","r",stdin);
// freopen("my.out","w",stdout);
n=read();
q=read();
for(int i=1;i<=n-1;i++){
fa[i+1]=read();
add(fa[i+1],i+1);
val[i+1]=read();
}
dfs(1,1);
int flag=0;
for(int i=1;i<=q;i++){
op=read();
if(op==1){
flag++;
u=read();
v=read();
w=read();
int uu=ask(u);
int vv=ask(v);
int ku=((dep[u]&1)==1?1:-1);
int kv=((dep[v]&1)==1?1:-1);
y=w-uu-vv;
x=ku+kv;
if(!x){
if(y)printf("none\n");
else printf("inf\n");
}
else if(y%x)printf("none\n");
else printf("%lld\n",y/x);
}
else{
u=read();
w=read();
if(dep[u]&1){
update(num[u],w-val[u]);
update(num[u]+size[u],val[u]-w);
}
else if(hd[u]){
update(num[edge[hd[u]].to],val[u]-w);
update(num[edge[hd[u]].to]+size[u]-1,w-val[u]);
}
val[u]=w;
}
}
return 0;
}
由于比较难调，还写了个对拍，可以配合食用由于比较难调，还写了个对拍，可以配合食用
#include<bits/stdc++.h>
using namespace std;
int main(){
freopen("shuju.in","w",stdout);
srand(time(0));
int n=rand()%10+2;
cout<<n<<endl;
int q=10;
cout<<q<<endl;
for(int i=2;i<=n;i++){
cout<<rand()%(i-1)+1<<" "<<rand()%10+1<<endl;
}
for(int i=1;i<=q;i++){
int op=rand()%2+1;
cout<<op<<" ";
if(op==1){
cout<<rand()%n+1<<" "<<rand()%n+1<<" "<<rand()%10+1<<endl;
}
else{
cout<<rand()%n+1<<" "<<rand()%10+1<<endl;
}
}
return 0;
}
C. Rectangle
暴力挂分中……
略……
update 8.9:
再次看 \(t3\)，终于理解了题解的思路
由于值域不大，可以 \(n^2\) 枚举横坐标，作为矩形的长
然后统计当前长下有多少对宽产生贡献
设横坐标为 \(l\) 和 \(r\) 的点，\(mx\) 为两者纵坐标最大值，\(mn\) 为最小值
那么产生的贡献为:
\(\displaystyle\sum_{y_i>mx}\sum_{y_j<mn}y_i-y_j\)
\(=\displaystyle\sum_{y_i>mx}y_i*siz_j-sum_j\)
\(=sum_i*siz_j-siz_i*sum_j\)
其中 \(siz\) 和 \(sum\) 分别表示点的个数和坐标和
发现这个式子用两个树状数组维护即可
但是如果对于 \(l\) 和 \(r\) 上有多个点的情况可能会算重
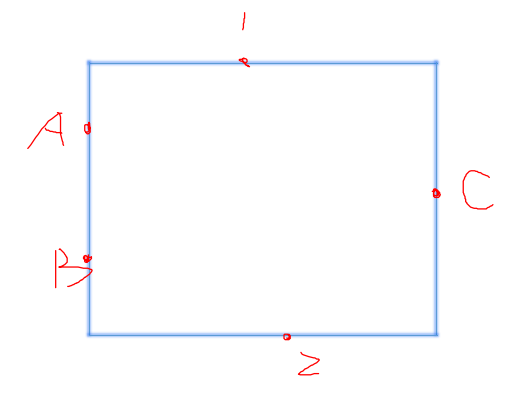
比如对于这个矩形，当标准点为 A、C 时会算到，而标准点为 B、C 的时候也会算到
那么可以把纵轴切割成一段一段的，然后分别计算：
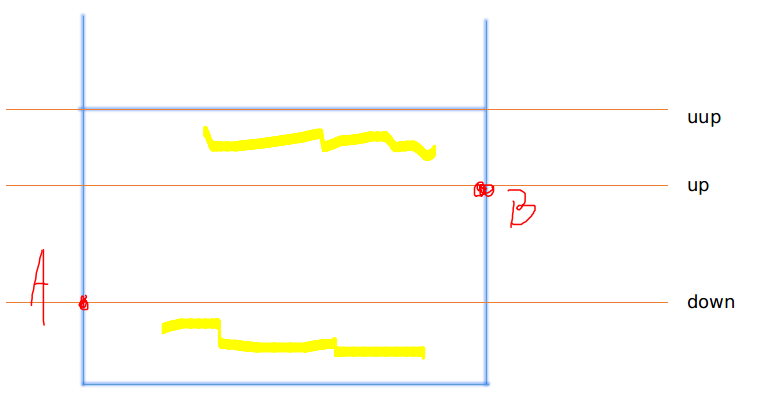
这样就可以有效解决重复问题
代码实现
#include<bits/stdc++.h>
using namespace std;
//#define int long long
const int mod=1e9+7;
const int MA=2500;
const int maxm=2505;
int n,c[maxm][maxm][2],x,y;
long long ans;
vector<int>a[maxm];
bool vis[maxm][maxm];
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
void add(int pos,int x,int w,int op){
for(;x<=MA;x+=x&-x)c[pos][x][op]+=w;
return ;
}
int ask(int pos,int x,int op){
int ans=0;
for(;x;x-=x&-x)ans+=c[pos][x][op];
return ans;
}
signed main(){
// freopen("shuju.in","r",stdin);
// freopen("my.out","w",stdout);
n=read();
for(int i=1;i<=n;i++){
x=read();
y=read();
a[x].push_back(y);
}
for(int i=1;i<=MA;i++){
sort(a[i].begin(),a[i].end());
a[i].push_back(MA+1);
}
// cout<<"hhh"<<endl;
for(int i=1;i<=MA;i++){
// cout<<i<<endl;
if(a[i].size()==1)continue;
for(int j=0;j<a[i].size()-1;j++){
if(!vis[i][a[i][j]]){
vis[i][a[i][j]]=true;
add(i,a[i][j],1,0);
add(i,a[i][j],a[i][j],1);
}
}
for(int j=i-1;j;j--){
if(a[j].size()==1)continue;
for(int k=0;k<a[j].size()-1;k++){
if(!vis[i][a[j][k]]){
vis[i][a[j][k]]=true;
add(i,a[j][k],1,0);
add(i,a[j][k],a[j][k],1);
}
}
int tp1=0,tp2=0,up=max(a[i][0],a[j][0]);
while(a[i][tp1+1]<=up)tp1++;
while(a[j][tp2+1]<=up)tp2++;
while(tp1<a[i].size()-1&&tp2<a[j].size()-1){
int uup=min(a[i][tp1+1],a[j][tp2+1]);
int down=min(a[i][tp1],a[j][tp2]);
// cout<<tp1<<" "<<tp2<<" "<<uup<<" "<<up<<endl;
ans=(ans+1ll*(i-j)*(
(ask(i,uup-1,1)-ask(i,up-1,1))*ask(i,down,0)-
(ask(i,uup-1,0)-ask(i,up-1,0))*ask(i,down,1)
))%mod;
up=uup;
if(a[i][tp1+1]<=up)tp1++;
if(a[j][tp2+1]<=up)tp2++;
}
}
}
cout<<ans<<endl;;
return 0;
}
Summary
-
T1 挂分比较严重，又一次死在了 long long 上……
-
T2 思路没有缕清，没有进一步思考
-
收获一枚 STL 神器——\(nth\_element\)
这场考试发挥极不好——恰逢一场春雨，是以乘意作《惊梦》篇：
惊梦时节起云烟，嫩柳清明蕴浽溦。
雨落应闻鹂莺叫，雁归本看杏花肥。
春秋丞案惜白羽，南北征途叹乌骓。
忍顾今夕杨柳岸，来斯何日雪霏霏。
