有日子没写博客了，这些天忙着一些杂七杂八的事情，直到某天，老师喊我好好把数据挖掘的算法搞一搞！于是便由再次埋头看起算法来！说起数据挖掘的算法，我想首先不得的不提起的就是大名鼎鼎的由决策树算法演化而来的C4.5算法，毕竟这是当年各个“鼻祖”在数据挖掘大会投票结果最高的一个算法了!
那我们现在就来具体看看C4.5算法到底是个什么东东？我想，首先我们应该提起的是决策树算法，我们首先要弄明白该算法的目的是什么，其本质目的实质就是预测！在一个系统当中，通过输入某些属性值可以预测出我们的预测属性！这么说可能有些绕，我们来举个现实点的例子来说明。
比如我们判断一个人能不能结婚，那么每个人就可以作为一个具体的对象，该对象有着很多属性，比如年龄，性别，帅不帅，工作NB不，有没有女朋友，是不是富二代6个属性，而结婚也作为该对象的一个属性，而”结婚”属性就可以作为我们的预测属性！然后根据其他属性来预测我们的目标属性--结婚属性，比如说，年龄：30，性别：男，长的帅，工作不错，又女朋友，还是富二代！根据这些属性我们就可以得出该人今年可以结婚！当然这是预测出来的！这时，我们肯定有个疑问了，这是如何预测的呢？这实质上是根据我们的统计数据得出的，比如我们统计10000个人，根据这一万个人的6个属性以及目标属性（结婚）最终得出一组数据，我们用这组数据做成一个决策树！而其中这10000个人的样本我们则称为训练样本！
我们还是拿”打高尔夫球”这个经典的例子来作具体研究吧!该例其实就是通过一些列的属性来决定是否适合打高尔夫！刚刚说了训练样本，我们就来看看训练样本吧！图1是我用WPF做了一个简单的CRUD界面，用来把我们的样本显示的展现出来。具体看图1。
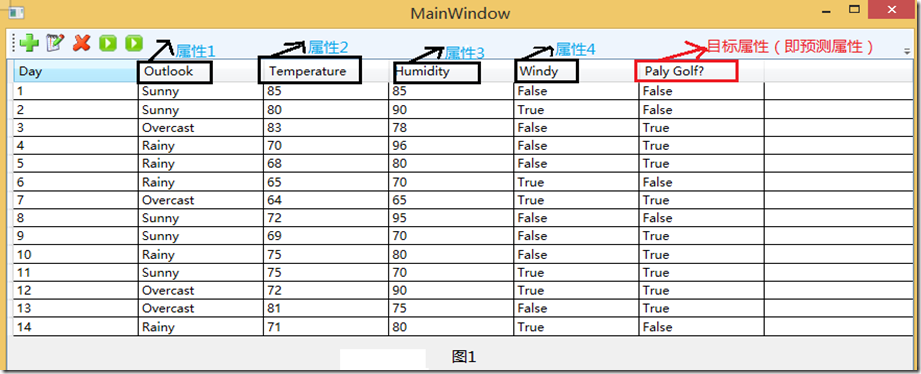
我们从图中可以看出，该表中共有6列，而每一列中的列名对应一个属性，而我们以实践经验知道，“Day”即日期这个属性并不能帮我们预测今天是否适合去打Golf.故该属性我们就应该选择摒弃！再看该系统中的其他5给属性。很显然，图1中我用红笔画出来的属性“Play Golf”该属性就是我们的预测属性。而其他4个属性“Outlook”（天气）”、Temperature”（温度） 、“Humdity”（湿度）、“Windy”(是否刮风)这四个属性进行判断今天去 Play Golf。
那我们接下来的工作自然就是根据属性1-4得出我们的决策树了!那么我们来想想该决策树的算法，实质上其遵循一种统一的递归模式：即，首先用根节点表示一个给定的数据集（比如在这，就是我们的14个样本）；然后，从根节点开始在每个节点上测试一个特定的属性，把节点数据集划分成更小的子集（这一步，比如根据属性Outlook划分，可以划分出三个子集出来，即属于Sunny的一个子集样本，属于Overcast的子集样本，属于Rainy的子集样本），该子集并用子树进行表示；该过程就开始一直进行，直到子集称为“纯的”,也就是说直到子集中的所有实例都属于同一个类别，树才停止生长。
看到这里，可能一些同学还不能理解什么才叫“纯”的，我们这里根据该算法推出一个决策树来，用图2表示，在这里，我们具体根据图来说明到底什么是“纯”的？先来看图2。
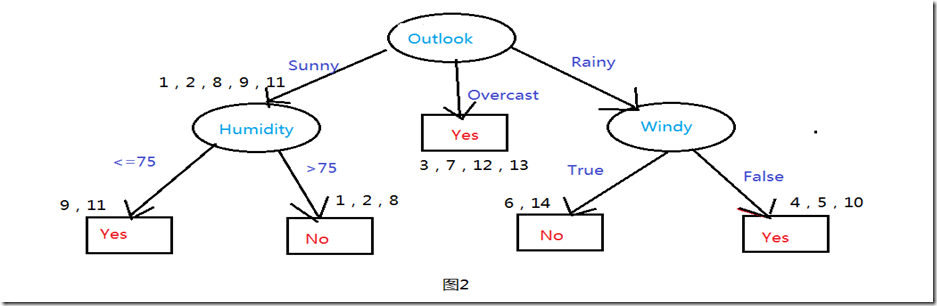
我们知道该数据集即有14个测试样例，所谓纯的数据集即使指最终的数据集所包含的每一个样例的最终预测属性值都是相同的（比如这里全部是Yes 或者全部是No）。比如样例3，7,12,13这四个样例的Play Golf值都是Yes。
我们看图2，首先是根据Outlook属性进行划分，根据Outlook的三个属性值（Sunny、Overcast、Rainy）划分出了三个组合，而其中Overcast划分中的集合是“纯”的了。故此子树就停止生长了。而根据Sunny属性值划分中的样例集合1，2，8，9，11显然还不是“纯”的（该组样例中有的PlayGolf是Yes,而有的是No）,故需要再次对其进行划分，直到分组中的所有样例都是“纯”的位置，才停止生长。
看到这里，你可能已经明白了该算法的过程。但是你马上在脑中就会蹦出一个问题来，那就是凭什么先要根据Outlook属性划分，怎么不是先是根据Humidity属性划分呢？总不能是随便根据一个属性就来划分吧！
在这里我们就需要引入一个信息论里面的概念了---熵。
信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序，信息熵就越低，反之，一个系统越是混乱，信息熵就越高。所以，信息熵也可以是系统有序化程度的一个度量。我们在这里，不妨把信息熵理解为某种特定信息的出现概率。
其具体的计算公式为：
H(x) = E[I(xi)] = E[ log(2,1/p(xi)) ] = -∑p(xi)log(2,p(xi)) (i=1,2,..n)
而在我们C4.5算法中，其目标就是通过合适的提问来获得信息，实现熵值的下降，我们依次考察每个属性，计算该属性导致的熵值下降幅度，而这个下降幅度我们称为信息增益。
其公式为：
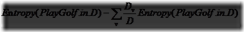
但实际上，信息增益并不能很正确的去预测，信息增益一般偏向于属性值多的属性。故我们一般采取的是更为准确的办法：那就是采取信息增益率，其定义为：
，其中，Gain(a)为属性a的信息增益,Entropy(a)为a的熵值。
之后，我们通过比较信息增益率，值最大的则为最佳节点。
说了这么多，我们还是上代码，具体来看如何来计算各个属性的信息增益率的！ 代码中有详细注释哦！
Codeusing System;
using System.Collections;
using System.Collections.Generic;
using System.Data;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace C4._5.BLL
{
public class Entropy
{
public int[] statNum = new int[2];//训练统计结果:0->No 1->Yes
public double EntropyValue = 0;
private int mTotal = 0;
private string mTargetAttribute = "PlayGolf";
public void getEntropy(DataTable samples)
{
CountTotalClass(samples,out statNum[0],out statNum[1]);
EntropyValue = CalcEntropy(statNum[0],statNum[1]);
}
/// <summary>
/// 统计各个样本集合中所包含的目标属性Yes或者No的数目
/// </summary>
public void CountTotalClass(DataTable samples,out int no,out int yes)
{
yes = no = 0;
foreach (DataRow aRow in samples.Rows)
{
if ((string)aRow[mTargetAttribute] == "Yes")
yes++;
else if ((string)aRow[mTargetAttribute] == "No")
no++;
else
throw new Exception("出错！");
}
}
/// <summary>
/// 计算熵值
/// </summary>
/// <returns></returns>
public double CalcEntropy(int no,int yes)
{
double entropy = 0;
double total = (double)(yes + no);
double p = 0;
if (no != 0)
{
p = no / total;
entropy += -p * Math.Log(p,2);
}
if (yes != 0)
{
p = yes / total;
entropy += -p * Math.Log(p, 2);
}
return entropy;
}
/// <summary>
/// 从属性中的样本集合中得到yes或者no的数目
/// </summary>
/// <param name="samples"></param>
/// <param name="attribute"></param>
/// <param name="value"></param>
/// <param name="no"></param>
/// <param name="yes"></param>
public void GetValuesToAttribute(DataTable samples, Attribute attribute, string value, out int no, out int yes)
{
no = yes = 0;
foreach (DataRow row in samples.Rows)
{
if ((string)row[attribute.AttributeName] == value)
{
if ((string)row[mTargetAttribute] == "No")
{
no++;
}
else if ((string)row[mTargetAttribute] == "Yes")
{
yes++;
}
else
{
throw new Exception("出错");
}
}
}
}
/// <summary>
/// 计算信息收益
/// </summary>
/// <param name="samples"></param>
/// <param name="attribute"></param>
/// <returns></returns>
public double Gain(DataTable samples, Attribute attribute)
{
mTotal = samples.Rows.Count;
string[] values=attribute.values;
double sum=0.0;
for (int i = 0; i < values.Length; i++)
{
int no, yes;
no = yes = 0;
GetValuesToAttribute(samples,attribute,values[i],out no,out yes);
if (yes == (yes + no) || no == (yes + no))
{
sum += 0;
}
else
{
sum += (double)(yes + no) / (double)mTotal * (-(double)yes / (double)(yes + no) * Math.Log(((double)yes / (double)(yes + no)), 2) - (double)no / (double)(yes + no) * Math.Log(((double)no / (double)(yes + no)), 2));
}
}
return SplitInfo(samples,mTargetAttribute)- sum;
}
/// <summary>
/// 获得targetAttribute属性下的所有属性值
/// </summary>
/// <param name="samples"></param>
/// <param name="targetAttribute"></param>
/// <returns></returns>
private ArrayList GetDistinctValues(DataTable samples, string targetAttribute)
{
ArrayList distinctValues = new ArrayList(samples.Rows.Count);
foreach (DataRow row in samples.Rows)
{
if (distinctValues.IndexOf(row[targetAttribute]) == -1)
distinctValues.Add(row[targetAttribute]);
}
return distinctValues;
}
/// <summary>
/// 按某个属性值计算该属性的熵值
/// </summary>
/// <param name="samples"></param>
/// <param name="attribute"></param>
/// <returns></returns>
public double SplitInfo(DataTable samples, string attribute)
{
ArrayList values = GetDistinctValues(samples,attribute);
for (int i = 0; i < values.Count; i++)
{
if (values[i] == null || (string)values[i] == "")
{
values.RemoveAt(i);
}
}
int[] count=new int[values.Count];
for (int i = 0; i < values.Count; i++)
{
foreach (DataRow aRow in samples.Rows)
{
if ((string)aRow[attribute] == (string)values[i])
count[i]++;
}
}
double entropy = 0;
double total = samples.Rows.Count;
double p = 0;
for (int i = 0; i < values.Count; i++)
{
if (count[i] != 0)
{
p = count[i] / total;
entropy += -p * Math.Log(p,2);
}
}
return entropy;
}
/// <summary>
/// 获得指定属性的信息增益率
/// </summary>
/// <param name="samples">样本集合</param>
/// <param name="attribute"></param>
/// <returns></returns>
public double GainRatio(DataTable samples, Attribute attribute)
{
double splitInfoA = this.SplitInfo(samples,attribute.AttributeName);//计算各个属性的熵值
double gainA = Gain(samples,attribute);//信息增益
double gainRatioA = gainA / splitInfoA;
return gainRatioA;
}
}
}
写到这里，我想一个关键的问题--如何选取最佳节点已经解决掉了，那么下一步就开始我们算法了！到底如何构造决策树呢？还记得刚刚说的递归模式吗！具体看代码吧！在代码中有详细的解释。
Code /// <summary>
/// 构造决策树
/// </summary>
/// <param name="samples">样本集合</param>
/// <param name="targetAttribute">目标属性</param>
/// <param name="attributes">该样本所含的属性集合</param>
/// <returns></returns>
private TreeNode BuildTree(DataTable samples, string targetAttribute, Attribute[] attributes)
{
TreeNode temp = new TreeNode();
//如果samples中的元祖是同一类C
string c = AllSamplesSameClass(samples,targetAttribute);
if (c != null) //返回N作为叶节点，以类C标记
return new TreeNode(new Attribute(c).AttributeName + c);
//if attributes为空，then
if (attributes.Length == 0)//返回N作为叶子节点，标记为D中的多数类，多数表决
{
return new TreeNode(new Attribute(GetMostCommonValue(samples,targetAttribute)).AttributeName);
}
//计算目标属性的熵值，即PlayGolf的熵值
mTargetAttribute = targetAttribute;
en.getEntropy(samples);
//找出最好的分类属性，即信息熵最大的
Attribute bestAttribute = getBestAttribute(samples,attributes);
//标记为节点root
DTreeNode root = new DTreeNode(bestAttribute);
temp.Text = bestAttribute.AttributeName;
DataTable aSample = samples.Clone();
//为bestAttribute的每个输出value划分元祖并产生子树
foreach (string value in bestAttribute.values)
{
aSample.Rows.Clear();
//aSamples为满足输出value的集合，即一个划分（分支）
DataRow[] rows = samples.Select(bestAttribute.AttributeName+"="+"'"+value+"'");
foreach (DataRow row in rows)
{
aSample.Rows.Add(row.ItemArray);
}
//删除划分属性
ArrayList aArributes = new ArrayList(attributes.Length-1);
for (int i = 0; i < attributes.Length; i++)
{
if (attributes[i].AttributeName != bestAttribute.AttributeName)
{
aArributes.Add(attributes[i]);
}
}
//如果aSample为空，加一个树叶到节点N，标记为aSample中的多数类
if (aSample.Rows.Count == 0)
{
TreeNode leaf = new TreeNode();
leaf.Text = GetMostCommonValue(samples, targetAttribute).ToString() + "(" + value + ")";
temp.Nodes.Add(leaf);
}
else //加一个由BulidTree(samples,targetAttribute,attributes)返回的节点到节点N
{
DTree_ID3 dc3 = new DTree_ID3();
TreeNode ChildNode = dc3.BuildTree(aSample,targetAttribute,(Attribute[])aArributes.ToArray(typeof(Attribute)));
ChildNode.Text += "(" + value + ")";
temp.Nodes.Add(ChildNode);
}
}
roots = temp;
return temp;
}
最终生成如图3的决策树。
既然生成了决策树，那么我们自然就要真正实时的来一把预测了！根据生成的决策树进行预测了！界面如图4所示。
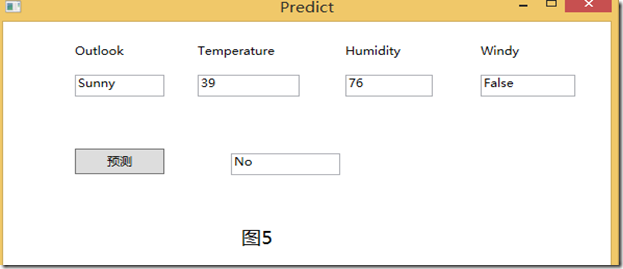
这时，我们在4个属性中输入我们所需输入的值，然后直接点击“预测”按钮就可以得到我们今天是否去PlayGolf! 如图5所示。
事实上，我们还没有对其预测的准确性进行判断，以及如何提高其准确性呢？那么下一篇将讲讲决策树剪枝来说明这一问题!
大功告成！不妨你也来试一把，看看你是否去PlayGolf！下面附上整个源码。
点击此处下载C4.5示例代码
