webgl变换:深入图形缩放
前言
关于图形的动画内容,之前已经分享完成了两篇,分别是webgl变换:深入图形平移和webgl变换:深入图形旋转。
在以往的学习中,大家都会发现一个问题,没有基础的知识,即使能学会,也会忘的很快。所以在之前的文章中,不仅跟大家介绍了如何通过矩阵实现图形的平移和旋转,也详细的分析了如何通过数学知识推导得到想要的矩阵。
也希望通过推导和矩阵的关联记忆,大家都可以将图形变换记忆和理解的更加深刻。
今天我们来分享下最后一个变换内容:图形的缩放 🤔
闲言少叙,来看第一个内容。
1.缩放矩阵
1.1 得到各坐标表达式
这里我们需要通过一个小实例来说明如何得到缩放矩阵
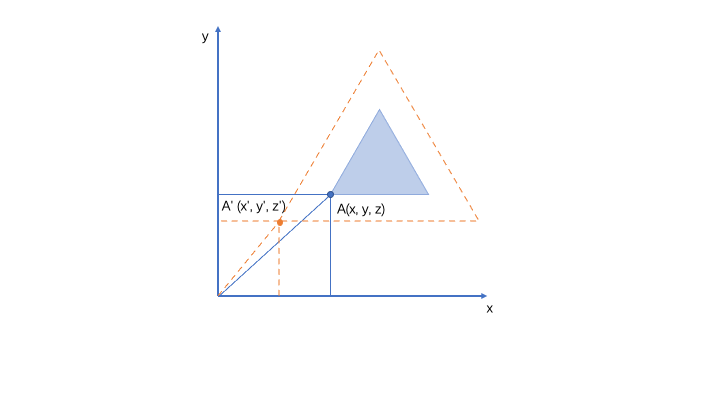
描述:
上图中,通过缩放,将蓝色三角形伸展到橙色虚线位置。
通过点A和点A’来观察三角形的坐标变化,我们可以得到如下等式:
x’ = Tx * xy’ = Ty * yz’ = Tz * z
1.2 查看点A和点A’之间的映射公式

通过上图,我们可以得到点A和点A’之间的关联计算关系
ax + by + cz + w = x'
ex + fy + gz + h = y'
ix + jy + kz + l = z'
mx + ny + oz + p = w'
ps: 这个公式我们已经写过很多次了 ,不明白的话可以看下之前的文章哟~~
1.3 得到缩放矩阵
将第一步和第二步得到的公式组合,可以得到如下等式:
ax + by + cz + w = Tx * x:只有当a = Tx,b = c = w = 0的时候,等式左右两边成立ex + fy + gz + h = Ty * y:只有当f = Ty, e = g = h = 0的时候,等式左右两边成立ix + jy + kz + l = Tx * z:只有当k = Tz, i = j = l = 0的时候,等式左右两边成立mx + ny + oz + p = 1:只有当m = n = o = 0, p = 1的时候,等式左右两边成立
经过处理,可得旋转矩阵为:
| Tx 0 0 0 |
| 0 Ty 0 0 |
| 0 0 Tz 0 |
| 0 0 0 1 |
可以看到,这个矩阵不论是行主序还是列主序。都是相等的,这种沿主对角线对称的矩阵,称为对称矩阵
2. 实践
1. 绘制一个三角形 (已经写烂了的代码~~)
const vertexShaderSource = "" +
"attribute vec4 apos;" +
"void main(){" +
" gl_Position = apos;" +
"}";
const fragmentShaderSource = "" +
"void main(){" +
" gl_FragColor = vec4(0.0,0.0,1.0,1.0);" +
"}";
const program = initShader(gl,vertexShaderSource,fragmentShaderSource);
const aposLocation = gl.getAttribLocation(program,'apos');
const data = new Float32Array([
0.0,0.3,
-.3,-.3,
.3,-.3
]);
const buffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER,buffer);
gl.bufferData(gl.ARRAY_BUFFER,data,gl.STATIC_DRAW);
gl.vertexAttribPointer(aposLocation,2,gl.FLOAT,false,0,0);
gl.enableVertexAttribArray(aposLocation);
gl.drawArrays(gl.TRIANGLES,0,3); // 第二步需要将此方法注释
2. 添加矩阵变量和绘制方式
因为矩阵会影响到所有顶点,所以我们使用 uniform 类型的数据。
const vertexShaderSource = "" +
"attribute vec4 apos;" +
"uniform mat4 mat;" + // 添加的矩阵变量
"void main(){" +
" gl_Position = mat * apos;" +
"}";
const matLocation = gl.getUniformLocation(program,'mat');
let Tx = 0; // x轴初始缩放
let Ty = 0; // y轴初始缩放
let Tz = 1; // z轴固定为1
let step = 0.06; // 每次的变化量
let status = true
function run () {
// 定义最大所放量为 2 倍
if (Tx >= 2) {
status = false
}
if (Tx <= 0) {
status = true
}
if (status) {
Tx += step;
Ty += step;
} else {
Tx -= step;
Ty -= step;
}
// 初始化一个旋转矩阵。
const mat = new Float32Array([
Tx, 0.0, 0.0, 0.0,
0.0, Ty, 0.0, 0.0,
0.0, 0.0, Tz, 0.0,
0.0, 0.0, 0.0, 1.0,
]);
// 将旋转矩阵赋值给着色器
gl.uniformMatrix4fv(matLocation,false,mat);
// 绘制新的三角形
gl.drawArrays(gl.TRIANGLES,0,3);
// 使用此方法实现一个动画
requestAnimationFrame(run)
}
run()
3. 效果演示

3. 总结
经过三篇文章的分享,我们已经得到了三种图形变换的矩阵,这里我们来总结一下:
1. 平移矩阵
| 1 0 0 x |
| 0 1 0 y |
| 0 0 1 z |
| 0 0 0 1 |
2. 旋转矩阵
| cos(β) sin(β) 0 0 |
| -sin(β) cos(β) 0 0 |
| 0 0 1 0 |
| 0 0 0 1 |
3. 缩放矩阵
| Tx 0 0 0 |
| 0 Ty 0 0 |
| 0 0 Tz 0 |
| 0 0 0 1 |
ps:旋转矩阵我们只推导了绕z轴旋转的矩阵。绕x轴和绕y轴的矩阵也可以自己试着推导下。
4. 完整代码
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Title</title>
</head>
<body>
<canvas id="webgl" width="500" height="500"></canvas>
<script>
const gl = document.getElementById('webgl').getContext('webgl');
const vertexShaderSource = "" +
"attribute vec4 apos;" +
"uniform mat4 mat;" +
"void main(){" +
" gl_Position = mat * apos;" +
"}";
const fragmentShaderSource = "" +
"void main(){" +
" gl_FragColor = vec4(0.0,0.0,1.0,1.0);" +
"}";
const program = initShader(gl,vertexShaderSource,fragmentShaderSource);
const aposLocation = gl.getAttribLocation(program,'apos');
const matLocation = gl.getUniformLocation(program,'mat');
const data = new Float32Array([
0.0,0.3,
-.3,-.3,
.3,-.3
]);
const buffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER,buffer);
gl.bufferData(gl.ARRAY_BUFFER,data,gl.STATIC_DRAW);
gl.vertexAttribPointer(aposLocation,2,gl.FLOAT,false,0,0);
gl.enableVertexAttribArray(aposLocation);
let Tx = 0; // x轴初始缩放
let Ty = 0; // y轴初始缩放
let Tz = 1; // z轴固定为1
let step = 0.06; // 每次的变化量
let status = true
function run () {
// 定义最大所放量为 2 倍
if (Tx >= 2) {
status = false
}
if (Tx <= 0) {
status = true
}
if (status) {
Tx += step;
Ty += step;
} else {
Tx -= step;
Ty -= step;
}
// 初始化一个旋转矩阵。
const mat = new Float32Array([
Tx, 0.0, 0.0, 0.0,
0.0, Ty, 0.0, 0.0,
0.0, 0.0, Tz, 0.0,
0.0, 0.0, 0.0, 1.0,
]);
// 将旋转矩阵赋值给着色器
gl.uniformMatrix4fv(matLocation,false,mat);
// 绘制新的三角形
gl.drawArrays(gl.TRIANGLES,0,3);
// 使用此方法实现一个动画
requestAnimationFrame(run)
}
run()
function initShader(gl,vertexShaderSource,fragmentShaderSource){
const vertexShader = gl.createShader(gl.VERTEX_SHADER);
const fragmentShader = gl.createShader(gl.FRAGMENT_SHADER);
gl.shaderSource(vertexShader,vertexShaderSource);
gl.shaderSource(fragmentShader,fragmentShaderSource);
gl.compileShader(vertexShader);
gl.compileShader(fragmentShader);
const program = gl.createProgram();
gl.attachShader(program,vertexShader);
gl.attachShader(program,fragmentShader)
gl.linkProgram(program);
gl.useProgram(program);
return program;
}
</script>
</body>
</html>



