最长公共子串(动态规划)

引言

最长公共子串

描述

有两个字符串，通过遍历找出最长的公共连续子串。

示例

输入两个字符串
abnacty
eabtnacm

输出最长公共连续子串
nac

分析

1. 将两个字符串分别以行和列的形式组成一个二维矩阵；
2. 比较二维矩阵中每个点对应的行和列的字符是否相等，相等的话，值设为1，不相等则为0；
3. 通过进一步查找，找出值为1的最长连续对角线就能找到最长公共子路

如图，给定两个字符串abcddf和acbcdf，求出其最长公共子串为 bcd

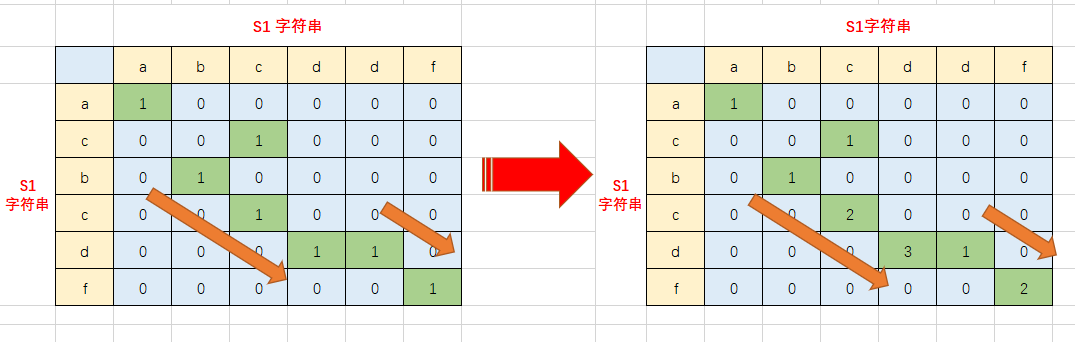
得出递推公式

//最长公共子串长度
maxLen = 0
//最长公共子串在a中的结束位置
endAIndex = 0
当 a[i] != b[j]时
  r[i] = 0
当 a[i] == b[j]时，
    若 i==0 或 j==0
        则r[i][j] = 1
    否
        r[i][j] = r[i-1][j-1] + 1

    如果r[i][j] > maxLen
        maxLen = r[i][j]
        endIndex = i

Java代码

public static String f(String s1, String s2) {
        if ("" == s1 || "" == s2) {
            return "";
        }
        //最长公共子串在S1串中的结束位置
        int endS1Index = 0;
        //最长公共子串的长度
        int maxLength = 0;
        int r[][] = new int[s1.length()][s2.length()];

        for (int i = 0; i < s1.length(); i++) {
            for (int j = 0; j < s2.length(); j++) {
                if (s1.charAt(i) != s2.charAt(j)) {
                    r[i][j] = 0;
                } else {
                    if (i == 0 || j == 0) {
                        r[i][j] = 1;
                    } else {
                        r[i][j] = r[i - 1][j - 1] + 1;
                    }
                    
                    if (maxLength < r[i][j]) {
                        maxLength = r[i][j];
                        endS1Index = i;
                    }
                }
            }
        }
        return s1.substring(endS1Index - maxLength+1, endS1Index+1);
    }