LCA（最近公共祖先）算法

首先看一下定义，来自于百度百科
LCA（Lowest Common Ancestors），即最近公共祖先，是指在有根树中，找出某两个结点u和v最近的公共祖先。
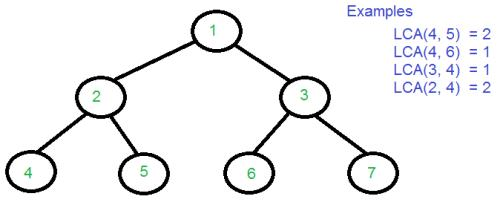注意：这里某个节点本身也是它的祖先节点。
求最近公共祖先的算法：
1.暴力：每次查询的时间复杂度为O(N)
2.Tarjan（离线）算法：在一次遍历中把所有查询解决，预处理时间复杂度O(nlogn),每次查询时间复杂度O(1)，总时间复杂度是O(nlogn+q)
3.倍增算法：利用二分两个节点同时往上走，直到相遇，预处理时间复杂度O(nlogn)，每次查询时间复杂度O(logn)

Tarjan（离线）算法

Tarjan算法大致实现过程

1.先选择一个节点u为根节点，从根节点开始搜索。（标记u已访问过）
2.遍历该点u的所有儿子节点v，并标记v已访问过。
3.若v还有儿子节点，对v重复ii操作，否则进入下一操作。
4.把v合并到u上（并查集）。
5.把当前的点设为u，遍历与u有询问关系的节点v。
6.如果v在之前已经被访问过，那么u和v的最近公共祖先就是v通过并查集合并后的父亲节点（注意是合并后），即当前的find（v）。

Tarjan算法的伪代码

Tarjan(u)           //根节点u
{
    for each(u,v)
    {
        Tarjan(v);  //v还有儿子节点
        join(u,v);  //把v合并到u上
        vis[v]=1;   //访问标记
    }
    for each(u,v)   //遍历与u有询问关系的节点v
    {
        if(vis[v])
        {
            ans=find(v);
        }
    }
}

Tarjan算法的代码

void Tarjan(int u)
{
    vis[u]=1;
    for(int i=0;i<mp[u].size();i++)
    {
        int v=mp[u][i];
        if(vis[v]==0)
        {
            Tarjan(v);
            join(u,v);
        }
    }
    for(int i=0;i<mp2[u].size();i++)//利用mp2集合来存储查询关系
    {
        int v=mp2[u][i];
        if(vis[v]==1)
        {
            lca[u][v]=find(v);
        }
    }
}

倍增算法

算法铺垫

分析刚才的算法，两个节点到达同一节点后，不论怎么向上走，达到的显然还是同一节点。利用这一点，我们就能够利用二分搜索求出到达最近公共祖先的最小步数了。
首先我们要进行预处理。对于任意的节点，可以通过fa2[v]=fa[fa[v]]得到其向上走2步到达的顶点，再利用这个信息，又可以通过fa4[v]=fa2[fa2[v]]得到其向上走4步所到的顶点。以此类推，我们可以得到其向上走2^k步所到的顶点fa[v][k],预处理的时间点复杂度为O(nlogn)。

void init()
{
    lg[1]=0;
    for(int i=2;i<=n;i++)
        lg[i]=lg[i-1]+(1<<(lg[i-1]+1)==i);//用来求log2(n)
}
void dfs(int f,int fath)
{
    deepth[f] = deepth[fath]+1;
    fa[f][0] = fath;
    for(int i = 1; (1<<i)<=deepth[f]; i++)
        fa[f][i] = fa[fa[f][i-1]][i-1];
    for(int i = 0; i < mp[f].size(); i++)
        if(mp[f][i] != fath)
            dfs(mp[f][i],f);
}
int lca(int x,int y)
{
    if(deepth[x]<deepth[y])
        swap(x,y);
    while(deepth[x]>deepth[y])
        x = fa[x][lg[deepth[x]-deepth[y]]];
    if(x==y)
        return x;
    for(ll k=lg[deepth[x]];k>=0;k--)
        if(fa[x][k]!=fa[y][k])
            x=fa[x][k], y=fa[y][k];
    return fa[x][0];
}