拟合

拟合与插值的不同

与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线拟合的最好（最小化损失函数）。

拟合的步骤

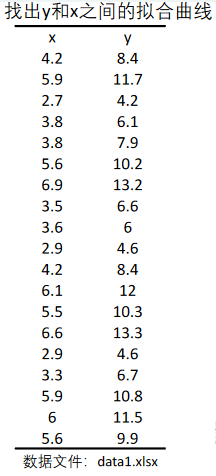
首先，我们需要绘制散点图，观察点的走向，选择合适的函数进行拟合

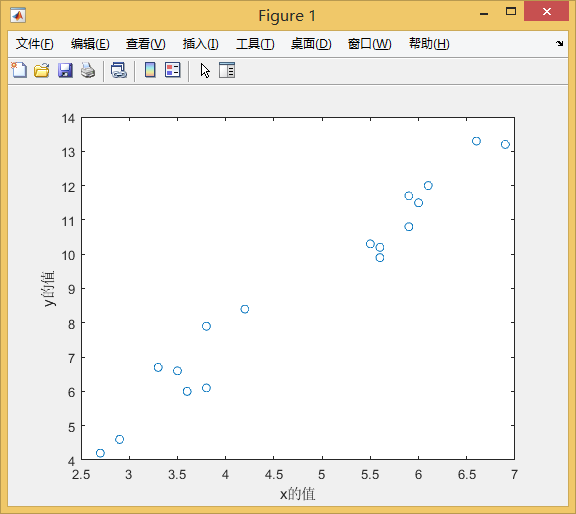这里我们选用一元函数 y=kx+b 进行拟合

使用最小二乘法进行拟合

最小二乘法的思想就是选择参数k和b使得y的实际值和y的估计值的平方和最小，用数学公式表达如下：
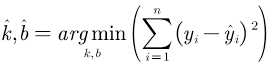求解的过程如下：
定义L，通过对k和b求导找到使得L最小的k和b

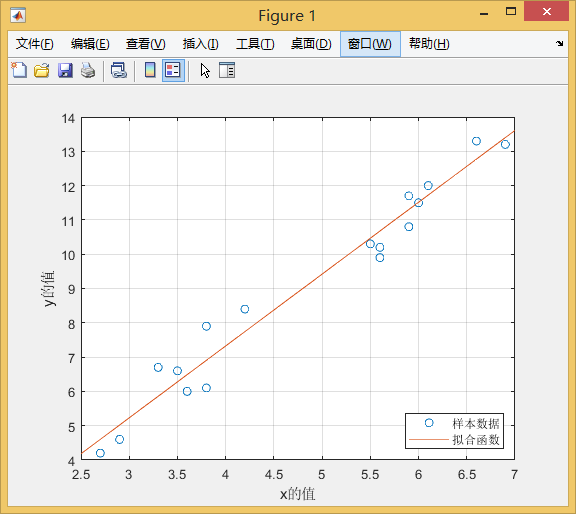
通过拟合优度评价拟合的好坏

拟合优度适用于线性函数，这里的线性指的是对参数线性。对参数线性是指，在函数中，参数仅以一次方出现，且不能乘以或除以其他任何的参数，并不能出现参数的复合函数形式。