插值

一、插值的定义

在离散数据的基础上补插连续函数，使得这条连续曲线通过全部给定的离散数据点。插值的目的是为了补齐样本数据或者对未来的数据进行预测。

一维插值问题的定义如下：

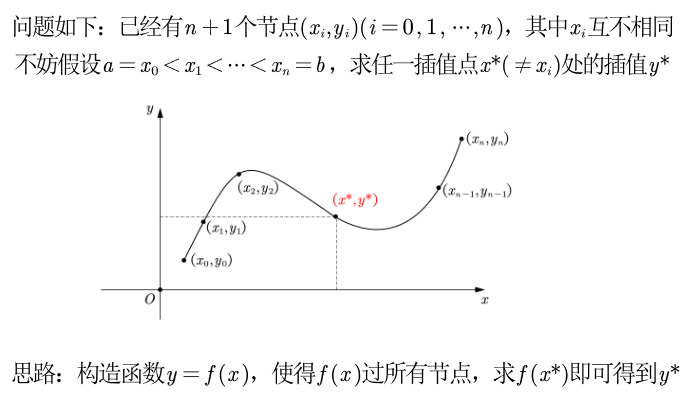
二、多项式插值

构造f(x)，使得f(x)满足以下形式：

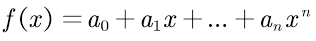
即为多项式插值。

解决多项式插值的方法有拉格朗日插值法和牛顿插值法。

（1）拉格朗日插值法

存在两个数据点f(x0,y0)和f(x1,y1)时

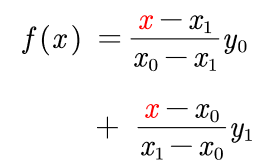
存在三个数据点f(x0,y0)、f(x1,y1)和f(x2,y2)时

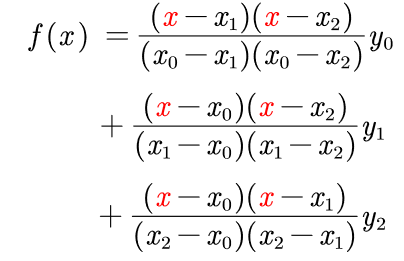
存在四个数据点f(x0,y0)、f(x1,y1)、f(x2,y2)和f(x3,y3)时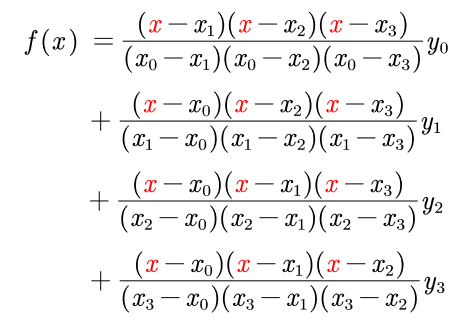

以此向下进行类推

（2）牛顿插值法

差商的定义：给定函数f(x)和插值节点用表示f(x)关于节点的k阶差商(k-th Difference Quotient)(k=1，2，…，n)，它们可递归定义为

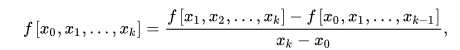
构造f(x)如下所示

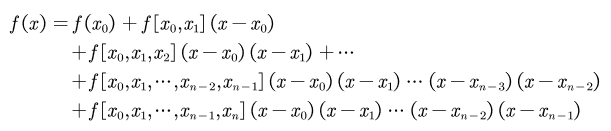
相比于拉格朗日插值法，牛顿插值法再增加第n+1个插值点时，可以重用第n个插值的数据，在原来的函数上添加新的项

 （3）龙格现象

在计算方法中，有利用多项式对某一函数的近似逼近，计算相应的函数值。一般情况下，多项式的次数越多，需要的数据就越多，而预测也就越准确。插值次数越高，插值结果越偏离原函数的现象称为龙格现象。（摘自百度百科）

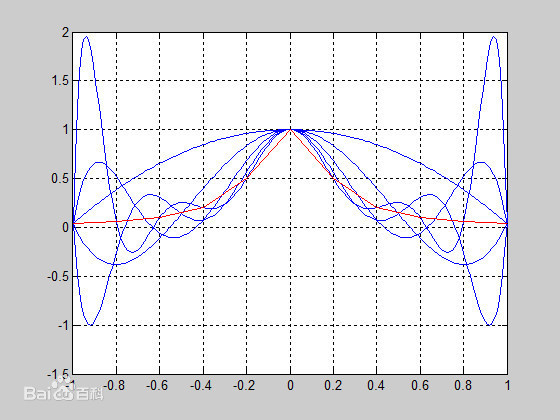
 为了避免高次多项式插值带来的龙格现象，往往采用分段低次插值

三、分段插值

（1）分段三次埃尔米特插值

埃尔米特插值的定义：不仅要求在节点上的函数值相等，而且还要求对应的导数值也相等,甚至要求高阶导数也相等，满足这种要求的插值多项式就是埃尔米特插值多项式。

直接使用Hermite插值得到的多项式次数较高，也存在着龙格现象，因此在实际应用中，往往使用分段三次Hermite插值多项式(PCHIP)。

matlab中有内置函数pchip(x,y, new_x)

其中x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标

matlab示例：

 

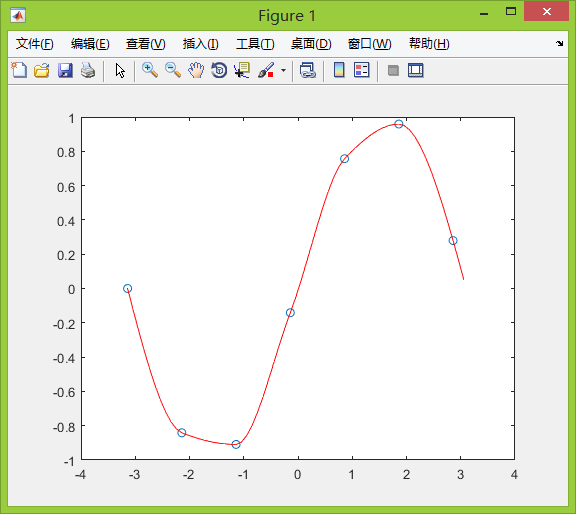
 （2）三次样条插值

三次样条插值定义：

 

 

 

 

 

 

 

matlab中有内置函数spline(x,y, new_x)

其中x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标

 

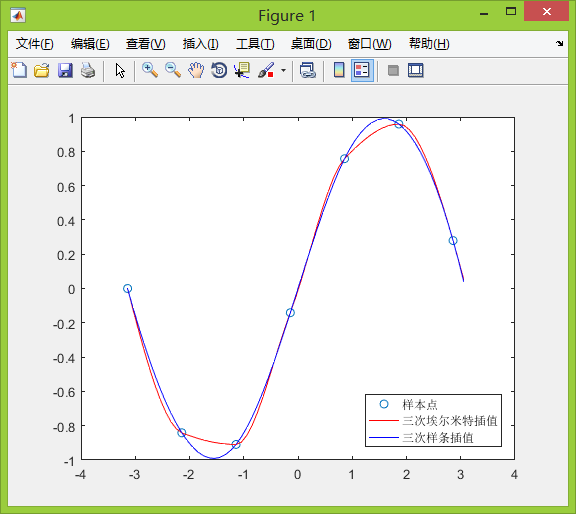
 相对于三次埃尔米特插值，三次样条插值更为平滑，在实际拟合过程中不知道数据的生成过程，因此两种插值均可使用