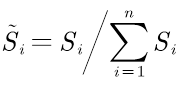优劣解距离法(TOPSIS)
一、模型介绍
TOPSIS 法是一种常用的综合评价方法,其能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。
基本过程为先将原始数据矩阵统一指标类型(一般正向化处理)得到正向化的矩阵,再对正向化的矩阵进行标准化处理以消除各指标量纲的影响,并找到有限方案中的最优方案和最劣方案,然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制,数据计算简单易行。
二、基本步骤
(一)将原始矩阵正向化
|
指标名称 |
指标特点 |
例子 |
|
极大型(效益型)指标 |
越大(多)越好 |
成绩、GDP增速、企业利润 |
|
极小型(成本型)指标 |
越小(少)越好 |
费用、坏品率、污染程度 |
|
中间型指标 |
越接近某个值越好 |
水质量评估时的PH值 |
|
区间型指标 |
落在某个区间最好 |
体温、水中植物性营养物量 |
所谓的将原始矩阵正向化,就是要将所有的指标类型统一转化为极大型指标,公式是不唯一的。
1)极小型指标->极大型指标
极小型指标转换为极大型指标的公式:

2)中间型指标->极大型指标
中间型指标:指标值既不要太大也不要太小,取某特定值最好(如水质量评估PH 值)
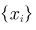 是一组中间型指标序列,且最佳的数值为,那么正向化公式如下:
是一组中间型指标序列,且最佳的数值为,那么正向化公式如下:
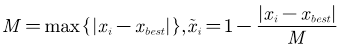
3)区间型指标
区间型指标:指标值落在某个区间内最好,例如人的体温在36°~37°这个区间比较好。

(二)正向化矩阵标准化
标准化的目的是消除不同指标量纲的影响。
假设有n个要评价的对象,m个评价指标(已经正向化了),构成的正向化矩阵如下:
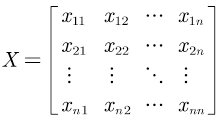 那么,对其标准化的矩阵记为Z,Z中的每一个元素:
那么,对其标准化的矩阵记为Z,Z中的每一个元素:
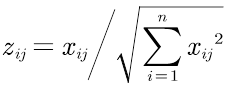
(每一个元素除以根号下每一列元素的平方和)
(三)计算得分并归一化
假设有n个评价对象,m个评价指标的标准化矩阵

定义最大值Z+=(Z1+,Z2+,..,Zm+)
=(max{z11,z21,..,zn1},max{z12,z22,..,zn2},...,max{z1m,z2m,..,znm})
定义最小值Z-=(Z1-,Z2-,..,Zm-)
=(min{z11,z21,..,zn1},min{z12,z22,..,zn2},...,min{z1m,z2m,..,znm})
定义第i(i=1,2,..,n)个评价对象与最大值的距离
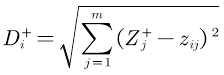
定义第i(i=1,2,..,n)个评价对象与最小值的距离
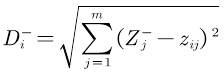
那么可以计算得出第i(i=1,2,..,n)个评价对象未归一化的得分
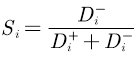
很明显0<=Si<=1,且Si越大Di+越小,即越接近最大值
将得分进行归一化