层次分析法(AHP)
一、模型介绍
层次分析法(简称AHP)的主要特点是通过建立递阶层次结构,把人类的判断转化到若干因素两两之间重要度的比较上,从而把难于量化的定性判断转化为可操作的重要度的比较上面。在许多情况下,决策者可以直接使用AHP进行决策,极大地提高了决策的有效性、可靠性和可行性,但其本质是一种思维方式,它把复杂问题分解成多个组成因素,又将这些因素按支配关系分别形成递阶层次结构,通过两两比较的方法确定决策方案相对重要度的总排序。
主要用于解决评价类问题(例如:选择哪种方案最好、哪位运动员或者员工表现的更优秀)。
评价类问题一般涉及三个要素
①评价的目标是什么
② 为了达到这个目标有哪几种可选的方案
③ 评价的准则或者说指标
二、具体步骤
1、分析系统中各因素之间的关系,建立系统的递阶层次结构
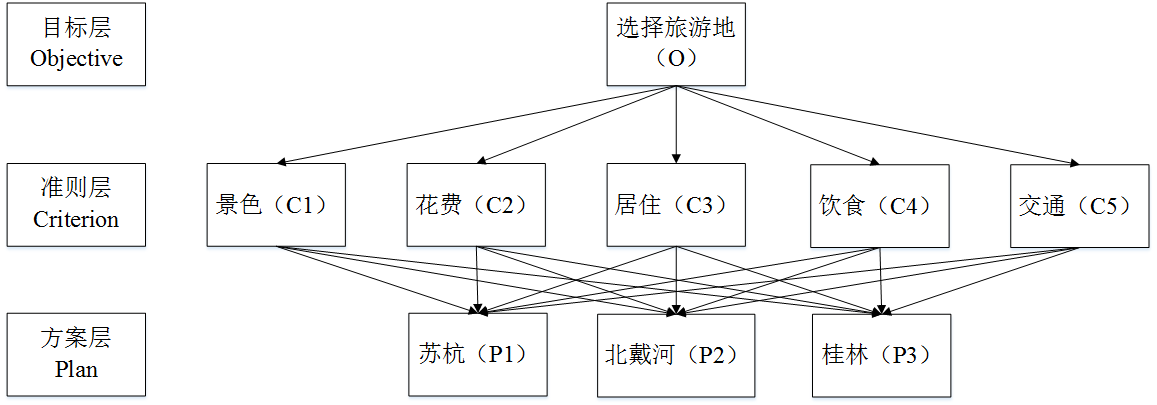
2、对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)。
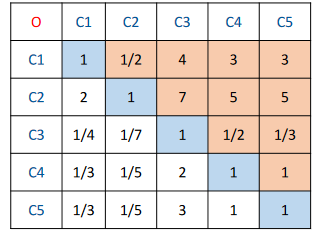
任何评价类模型都具有主观性:理想:采用专家群体判断现实:几乎都是自己填的
3、由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验(检验通过权重才能用)。
三种方法计算权重:(1)算术平均法(2)几何平均法(3)特征值法
4、一致性检验的步骤
第一步:计算一致性指标CI

第二步:查找对应的平均随机一致性指标RI

注:在实际运用中,n很少超过10,如果指标的个数大于10,则可考虑建立二级指标体系,或使用模糊综合评价模型。
第三步:计算一致性比例CR
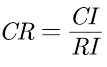
如果CR < 0.1, 则可认为判断矩阵的一致性可以接受;否则需要对判断矩阵进行修正。
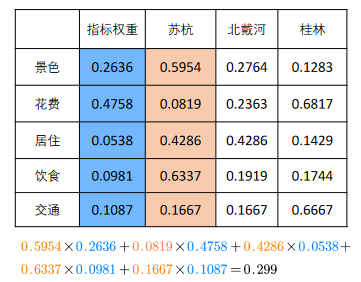
5、根据权重矩阵计算得分,并进行排序。