什么是梯度
向量的内积
a、 b 的内积 a · b 的定义如下所示:

注:当 a、 b 有一个为 0 或两者都为 0 时,内积定义为 0。
柯西 - 施瓦茨不等式
根据内积的定义式,我们可以推导出下式:
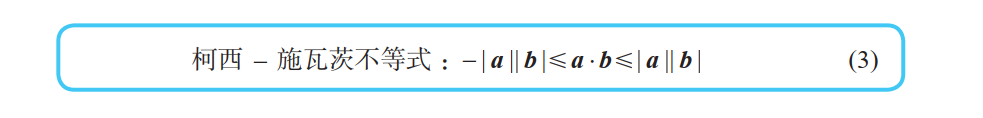
证明:
根据余弦函数的性质,对任意的 θ,有 - 1 ≤ cosθ ≤ 1,两边同时乘以 | a || b |,有:
利用定义式 (2),我们可以得到式 (3),证毕。
当两个向量a、b大小固定时,有下面三种情况:
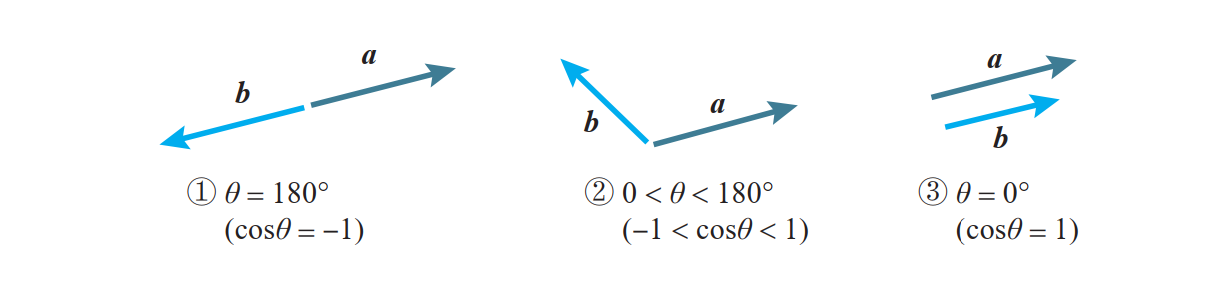
根据柯西 - 施瓦茨不等式 (3),可以得出以下事实:
①当两个向量方向相反时,内积取得最小值。【梯度下降法的基本原理】
②当两个向量不平行时,内积取平行时的中间值。
③当两个向量方向相同时,内积取得最大值。
向量的一般化
向量的方便之处在于,二维以及三维空间中的性质可以照搬到任意维空间中。神经网络虽然要处理数万维的空间,但是二维以及三维空间的向量性质可以直接利用。出于该原因,向量被充分应用在后述的梯度下降法中。
将二维以及三维空间中的向量公式推广到任意的 n 维空间:

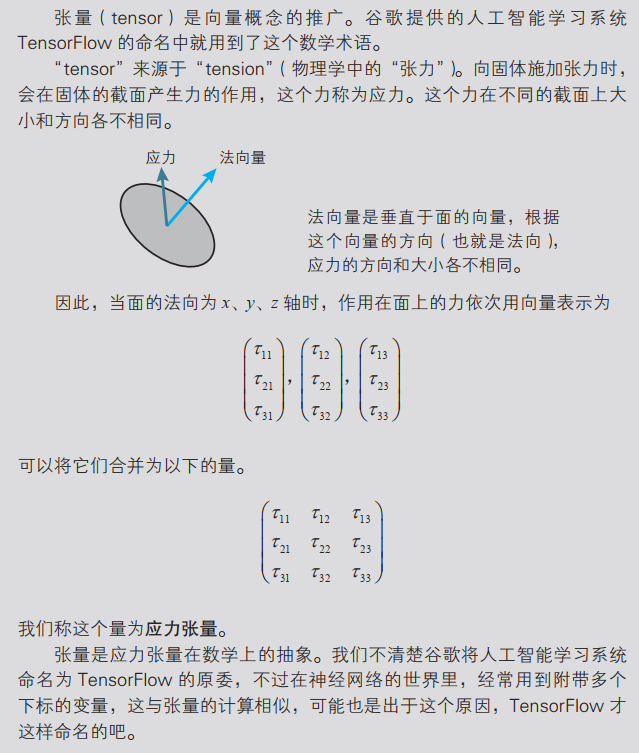
张量
导数的定义
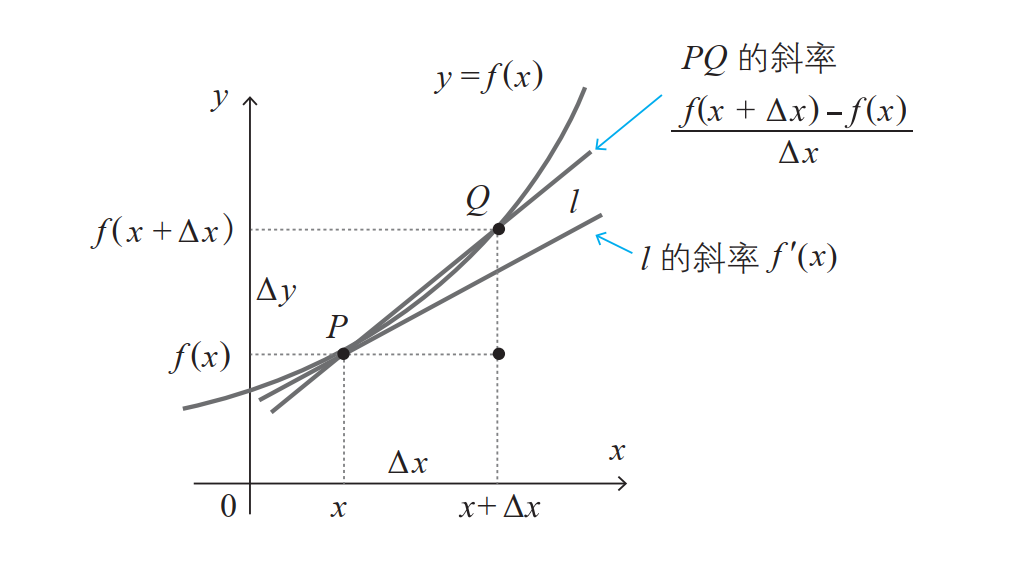
函数 y =f (x) 的导函数 f '(x) 的定义如下所示:
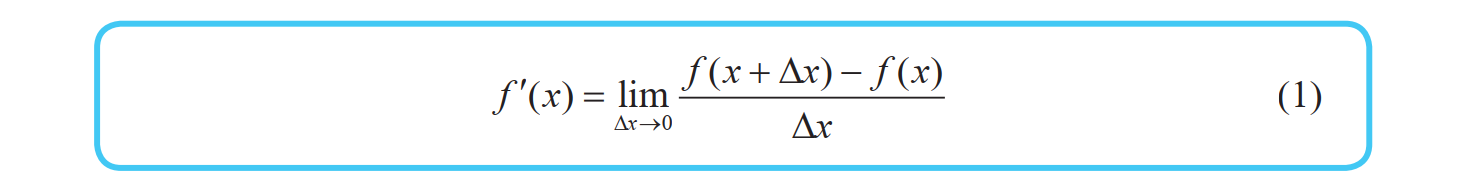
注:希腊字母 ∆ 读作 delta,对应拉丁字母 D。此外,带有 '(prime)符号的函数或变量表示导函数。
已知函数 f (x),求导函数 f '(x),称为对函数 f (x) 求导。当式 (1) 的值存在时,称函数可导。
导函数的含义如下图所示。作出函数 f (x) 的图像, f '(x) 表示图像切线的斜率。因此,具有光滑图像的函数是可导的。
导数符号
函数 y = f (x) 的导函数用 f '(x) 表示,但也存在不同的表示方法,例如可以用如下的分数形式来表示:
导数的性质
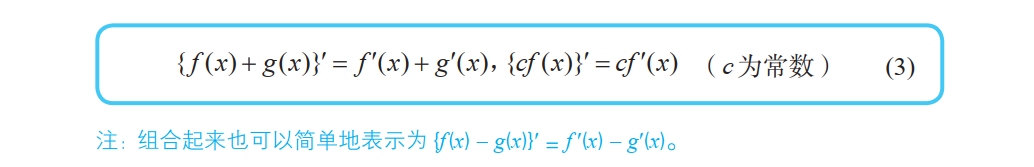
式 (3) 称为导数的线性性。
分数函数的导数和 Sigmoid 函数的导数
当函数是分数形式时,求导时可以使用下面的分数函数的求导公式:

Sigmoid 函数 σ(x) 是神经网络中最有名的激活函数之一,其定义如下所示:
在后述的梯度下降法中,需要对这个函数求导。求导时使用下式会十分方便。
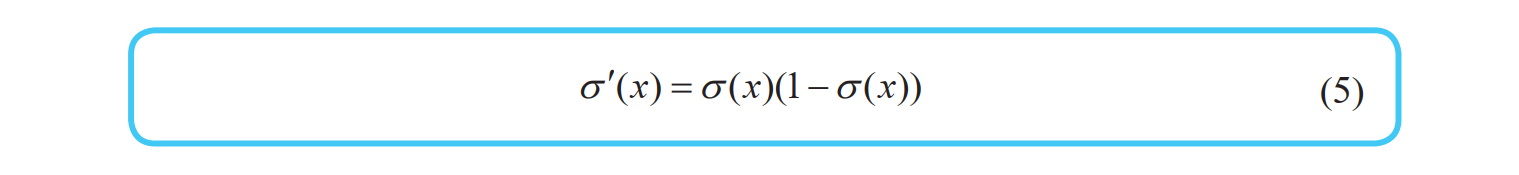
证明:
将 \(1+e^{-x }\)带入式(4)的 f(x),在利用导数公式:\((e^{-x })^{'} = -e^{-x}\),可得
证毕!
最小值的条件
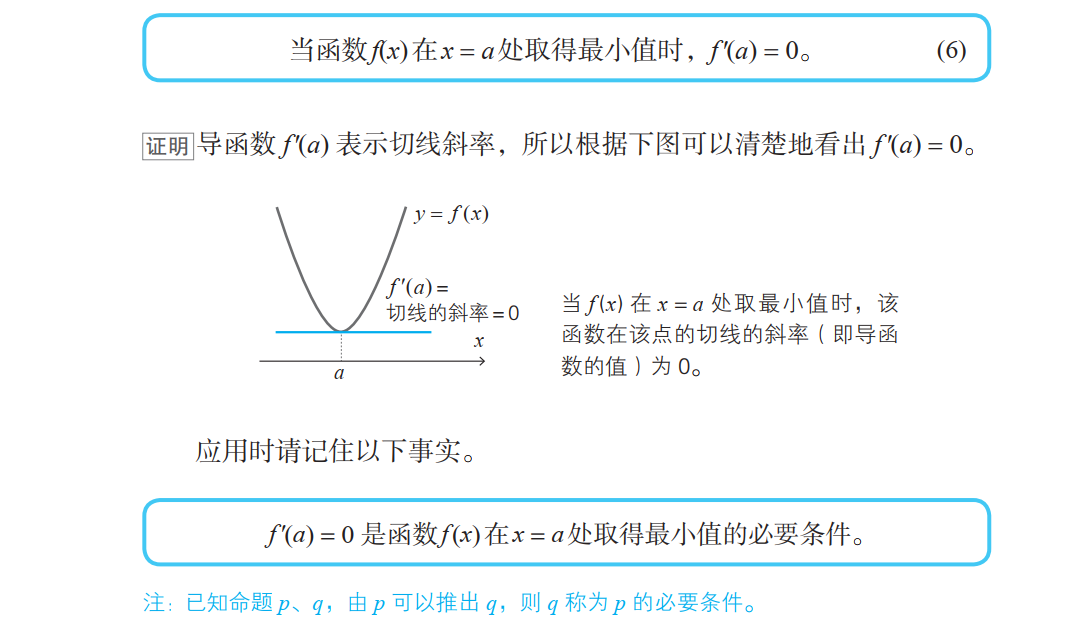
因为存在下面的函数:
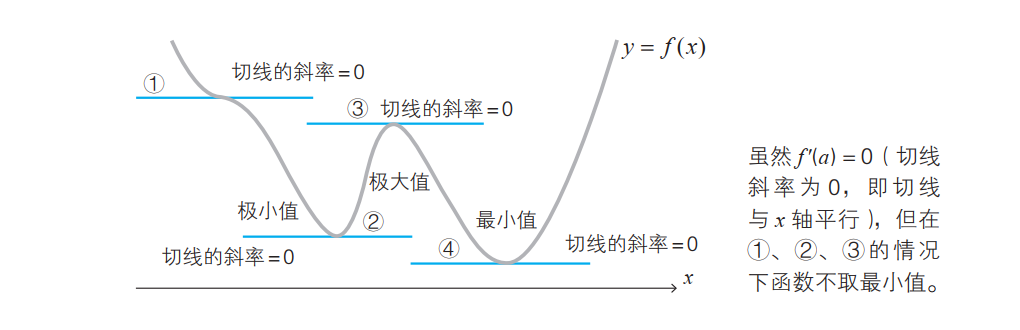
偏导数
关于某个特定变量的导数就称为偏导数( partial derivative)
例如,让我们来考虑有两个变量 x、 y 的函数 z = f (x, y)。只看变量 x,将 y 看作常数来求导,以此求得的导数称为“关于 x 的偏导数”,用下面的符号来表示:
关于 y 的偏导数也是同样的:
举例:

多变量函数的最小值条件
光滑的单变量函数 y = f (x) 在点 x 处取得最小值的必要条件是导函数在该点取值 0 ,这个事实对于多变量函数同样适用。例如对于有两个变量的函数,可以如下表示:

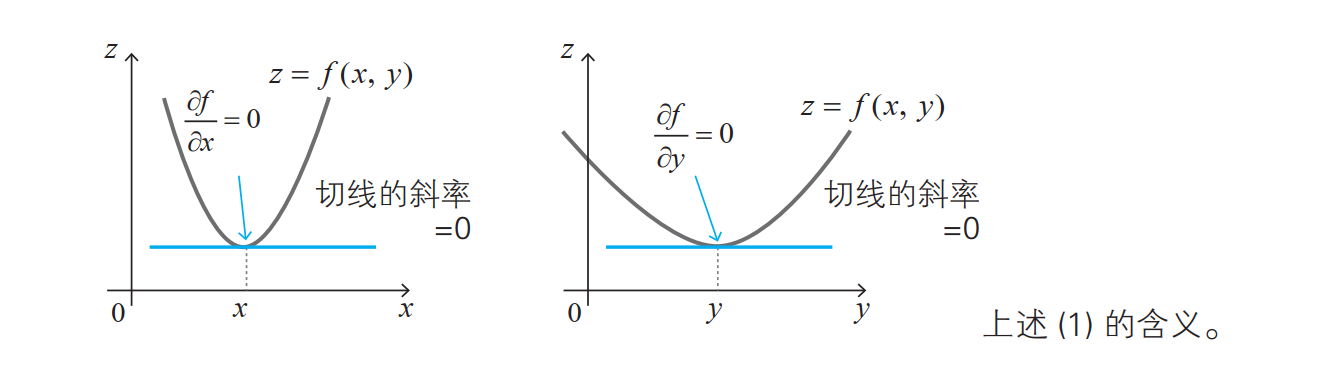
链式法则
单变量函数的链式法则
已知单变量函数 y = f (u),当 u 表示为单变量函数 u = g(x) 时,复合函数 f (g(x)) 的导函数可以如下简单地求出来:
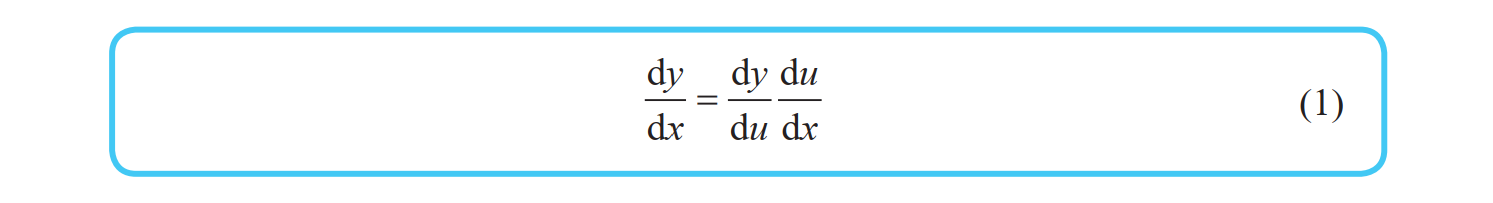
这个公式称为单变量函数的复合函数求导公式,也称为链式法则。
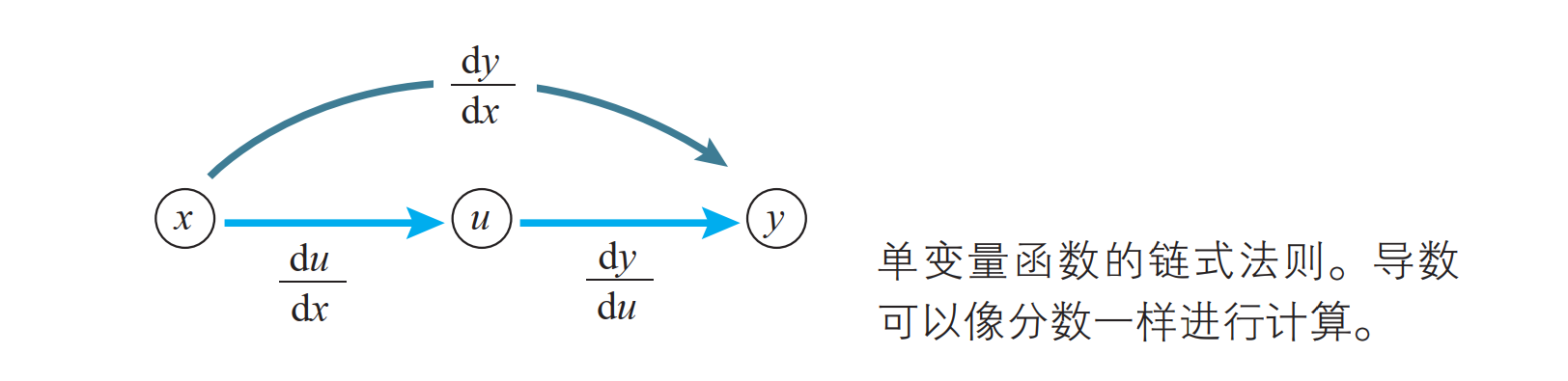
多变量函数的链式法则
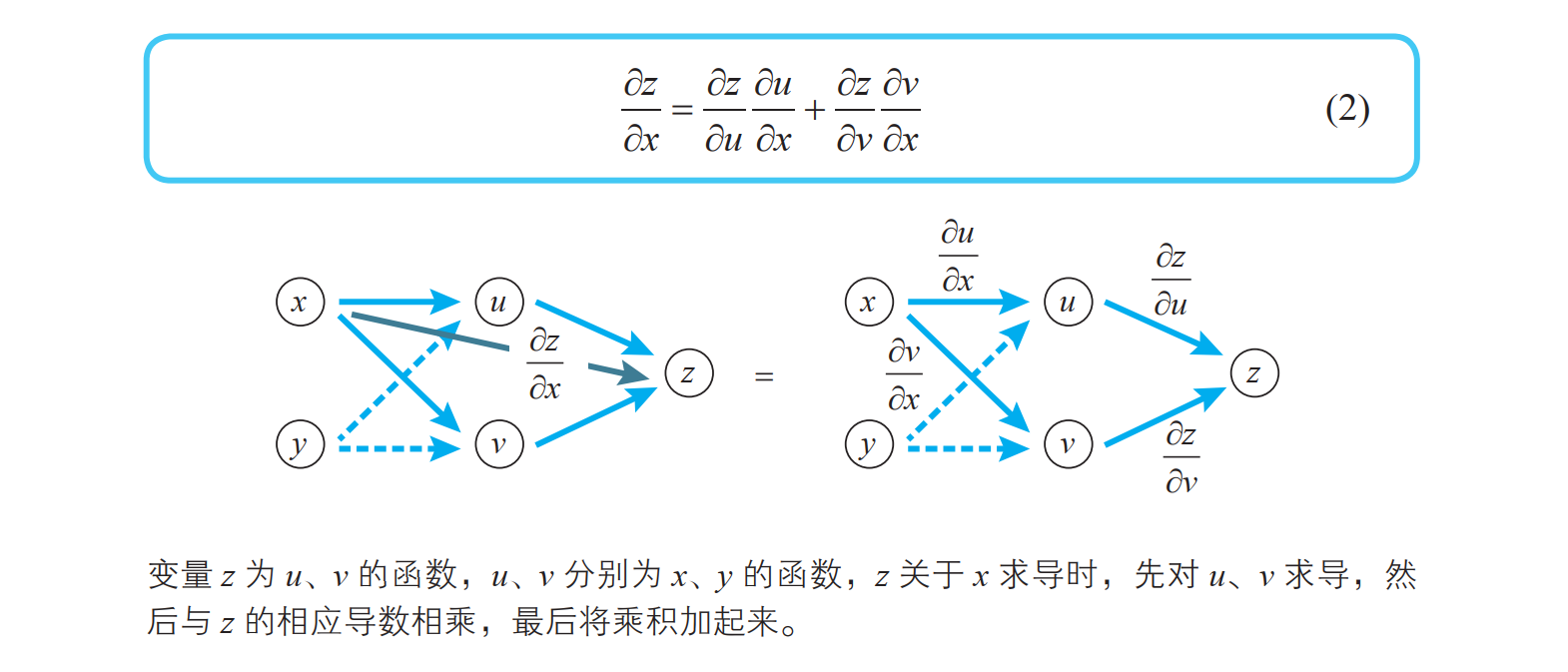
变量 z 为 u、 v 的函数,如果 u、 v 分别为 x、 y 的函数,则 z 为 x、 y的函数,此时下式( 多变量函数的链式法则)成立:
梯度下降法的基础
单变量函数的近似公式
首先我们来考察单变量函数 y = f(x)。如果 x 作微小的变化,那么函数值 y 将会怎样变化呢?答案就在导函数的定义式中:
在这个定义式中, ∆x 为“无限小的值”,不过若将它替换为“微小的值”,也不会造成很大的误差。因而,下式近似成立:
注意:\(≒\) 表示近似于
将上式变形,可以得到以下单变量函数的近似公式:
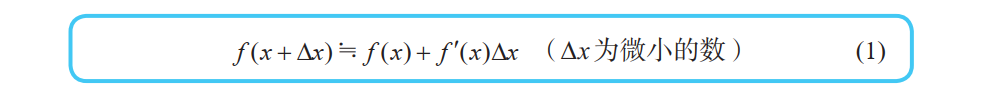
举例:
当 \(f(x) = e^x\) 时, x = 0 附近的近似公式为:
取x=0,重新\(\bigtriangleup x\)将替换为x,可得:
其几何意义如下:

多变量函数的近似公式
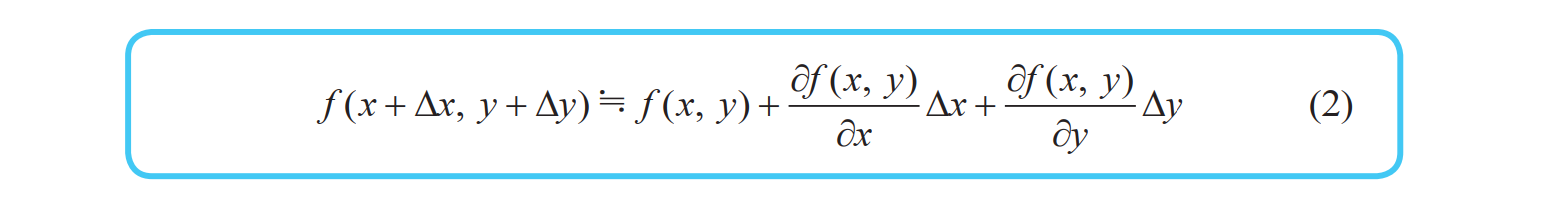


近似公式的向量表示
三个变量的函数的近似公式 (4) 可以表示为如下两个向量的内积∇z ⋅∆ x 的形式:
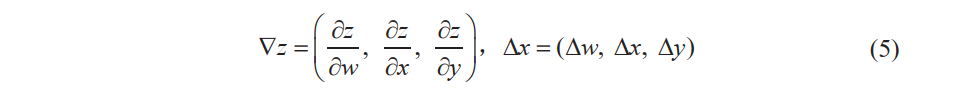
梯度下降法的含义与公式
梯度下降法的思路
已知函数 z = f(x, y),怎样求使函数取得最小值的 x、 y 呢?最有名的方法就是利用“使函数 z = f (x, y) 取得最小值的 x、 y 满足以下关系”这个事实:
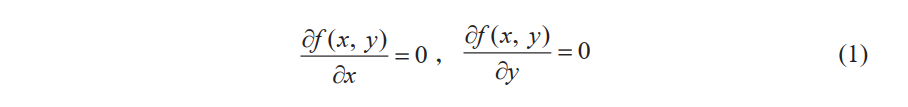
这是因为,在函数取最小值的点处,就像葡萄酒杯的底部那样,与函数相切的平面变得水平。
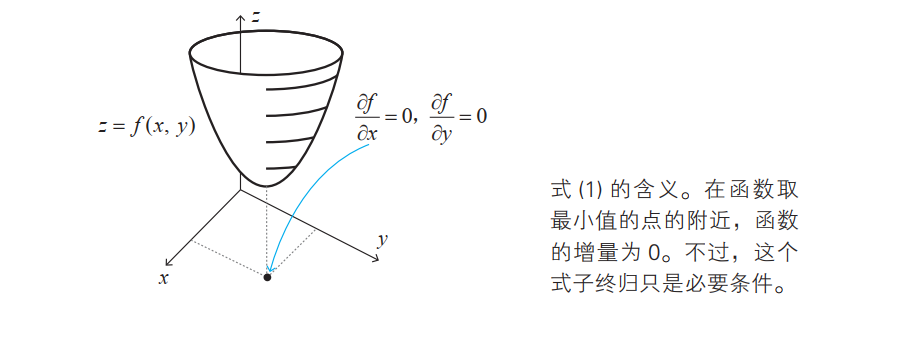
近似公式和内积的关系
函数 z = f(x, y) 中,当 x 改变 ∆x, y 改变 ∆y 时,我们来考察函数 f(x, y) 的值的变化 ∆z。
根据近似公式,以下关系式成立:
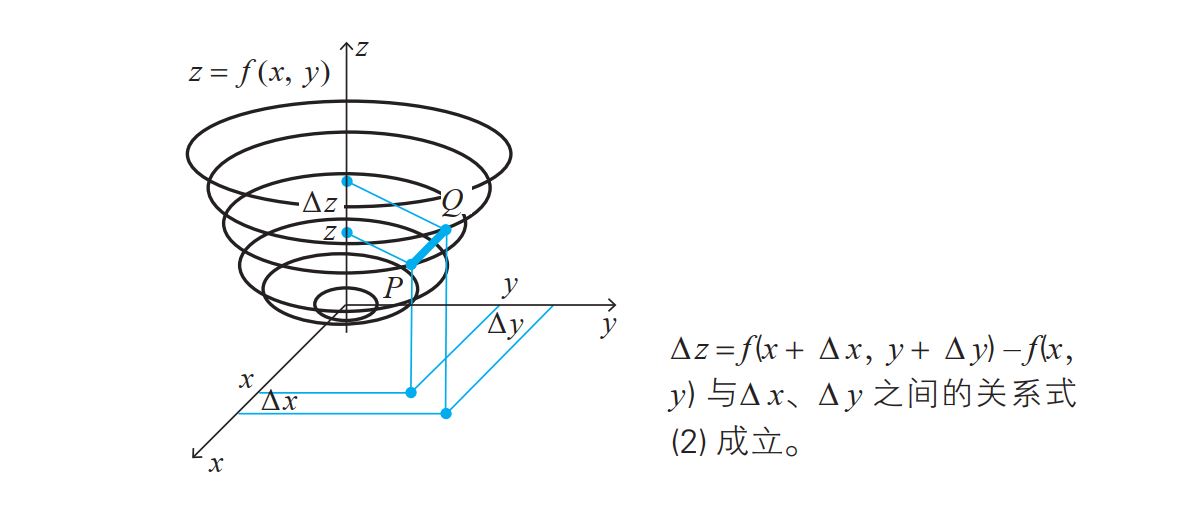
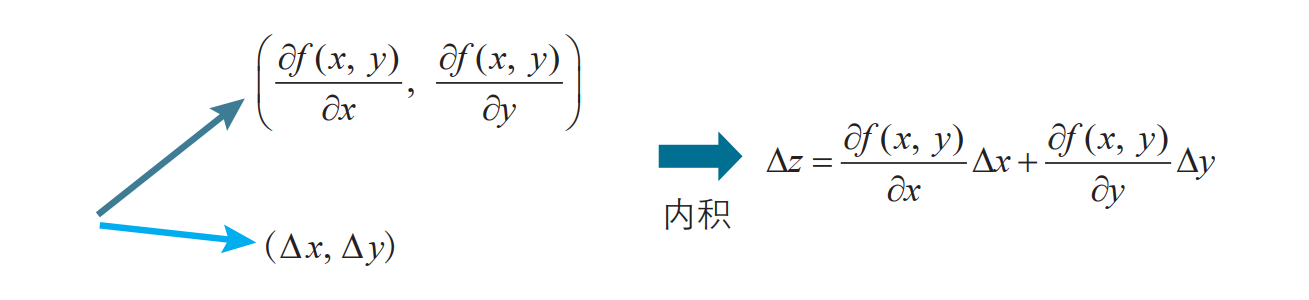
\(\bigtriangleup z=\frac{\partial f(x,y) }{\partial x} \bigtriangleup x+\frac{\partial f(x,y) }{\partial y} \bigtriangleup y\) 的右边可以表示为如下两个向量的内积形式:
请大家注意这个内积的关系,这就是梯度下降法的出发点。
我们来考察两个固定大小的非零向量 a、 b。当 b 的方向与 a 相反时,内积 a · b 取最小值:
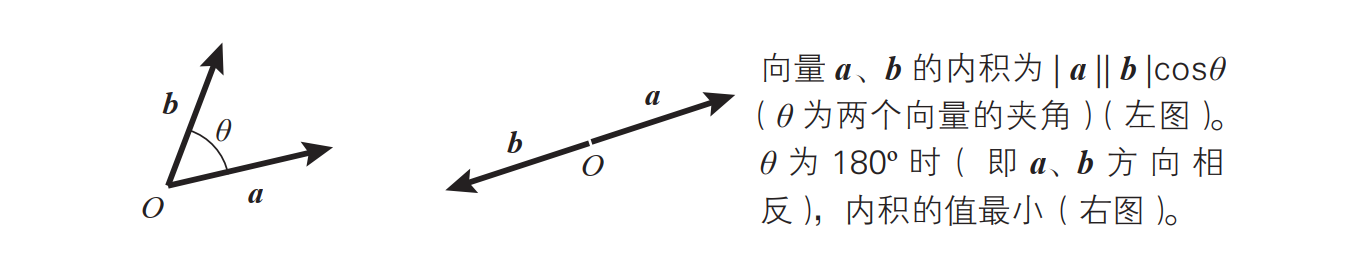
换句话说,当向量 b 满足以下条件式时,可以使得内积 a · b 取最小值:
内积的这个性质就是梯度下降法的数学基础。
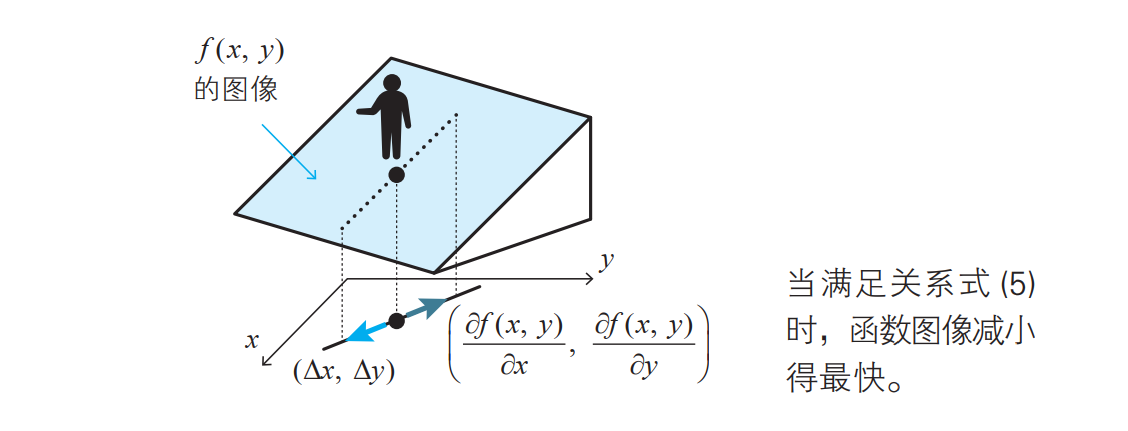
根据上面我们可以知道,从点 (x, y) 向点 (x + ∆x, y + ∆y) 移动时,当满足以下关系式时,函数 z = f (x, y) 减小得最快。这个关系式就是二变量函数的梯度下降法的基本式:
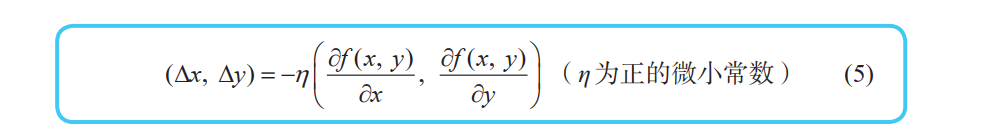
如果从点 (x, y)向点(x + ∆x, y + ∆y)移动就可以从图像上点 (x, y) 的位置最快速地下坡。
右边的向量 \((\frac{\partial f(x,y) }{\partial x},\frac{\partial f(x,y) }{\partial y} )\) 称为函数 f (x, y) 在点 (x, y) 处的梯度( gradient)。这个名称来自于它给出了最陡的坡度方向。
将梯度下降法推广到三个变量以上的情况
当函数 f 由 n 个自变量 x1, x2, …, xn 构成时,梯度下降法的基本式可以像下面这样进行推广:

哈密顿算子\(\bigtriangledown\)
在实际的神经网络中,主要处理由成千上万个变量构成的函数的最小值。在这种情况下,像式上面 (7) 那样的表示往往就显得十分冗长。因此我们来考虑更简洁的表示方法。
在数学的世界中,有一个被称为向量分析的领域,其中有一个经常用到的符号 ∇ 。 ∇ 称为哈密顿算子,其定义如下所示:
利用这个符号,式 (7) 可以如下表示:
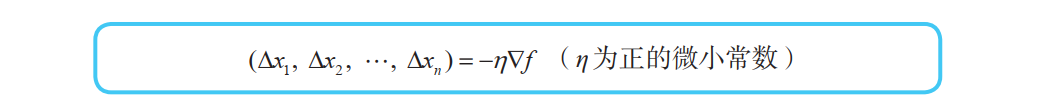
其中,左边的向量 (∆x1, ∆x2, …, ∆xn) 称为位移向量,记为 ∆x。
利用这个位移向量,梯度下降法的基本式 (7) 可以更简洁地表示:

η 可以看作人移动时的“步长”,根据 η 的值,可以确定下一步移动到哪个点。
如果步长较大,那么可能会到达最小值点,也可能会直接跨过了最小值点(左图)。
而如果步长较小,则可能会滞留在极小值点(右图)。
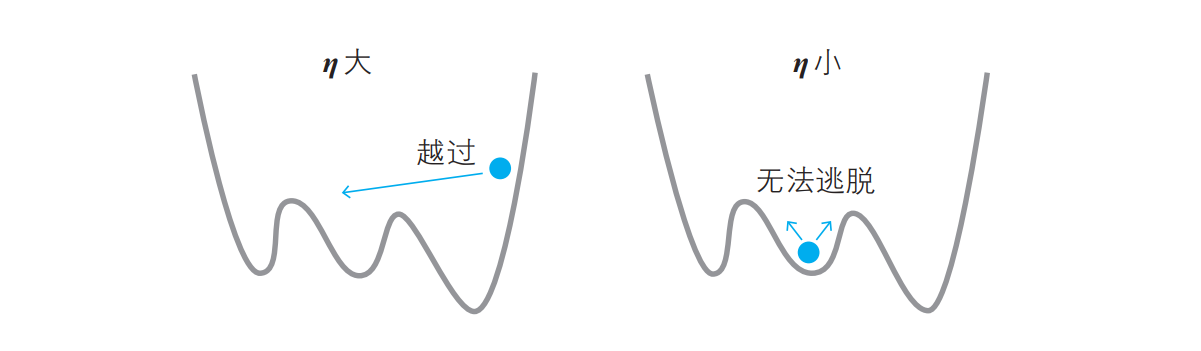
在神经网络的世界中, η 称为学习率。遗憾的是,它的确定方法没有明确的标准,只能通过反复试验来寻找恰当的值。
\(f(x_0+x_1)= x_0^{2}+x_1^{2}\)的梯度呈现为有向向量(箭头)。观察下图,
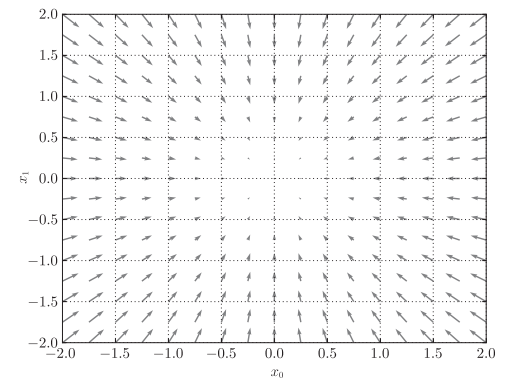
我们发现梯度指向函数\(f(x_0+x_1)\)的“最低处”(最小值),就像指南针一样,所有的箭头都指向同一点。其次,我们发现离“最低处”越远,箭头越大。
实际上,梯度会指向各点处的函数值降低的方向。更严格地讲,梯度指示的方向是各点处的函数值减小最多的方向
在复杂的函数中,梯度指示的方向基本上都不是函数值最小处。
函数的极小值、最小值以及被称为鞍点(saddle point) 的地方,梯度为0。
极小值是局部最小值,也就是限定在某个范围内的最小值。
鞍点是从某个方向上看是极大值,从另一个方向上看则是极小值的点。
虽然梯度法是要寻找梯度为0的地方,但是那个地方不一定就是最小值(也有可能是极小值或者鞍点)。
此外,当函数很复杂且呈扁平状时,学习可能会进入一个(几乎)平坦的地区,陷入被称为“学习高原”的无法前进的停滞期。
参考:
[1]深度学习的数学/(日)涌井良幸,(日)涌井贞美著;杨瑞龙译.--北京:人民邮电出版社,2019.5
[2]深度学习入门:基于Python的理论与实现/(日)斋藤康毅著;陆宇杰译.--北京:人民邮电出版社,2018.7


 浙公网安备 33010602011771号
浙公网安备 33010602011771号