激活函数（ activation function）

目录

• 单位阶跃函数
  • Python实现
• Sigmoid函数
  • Python实现
• ReLU函数
  • Python实现
  • 从ReLU衍生的激活函数
• softmax函数
  • Python实现
  • 改进softmax函数
  • softmax函数的特征

---

返回 我的研究方向(Research Interests)

---

单位阶跃函数

定义如下：

\[u(x)=\begin{cases} 0 & \text{ if } x=0 \\ 1 & \text{ if } x≥0 \end{cases} \]

从这个式子我们可以知道，单位阶跃函数在原点处不连续，也就是在原点不可导。由于这个不可导的性质，单位阶跃函数不能成为主要的激活函数。

Python实现

def step_function(x):
    return np.array(x > 0, dtype=np.int)

解释：

>>> import numpy as np
>>> x = np.array([-1.0, 1.0, 2.0])
>>> x
array([-1., 1., 2.])
>>> y = x > 0
>>> y
array([False, True, True], dtype=bool)
>>> y = y.astype(np.int)
>>> y
array([0, 1, 1])

Sigmoid函数

定义如下：

\[\sigma (z) = \frac{1}{1+e^{-z}} (e=2.718281...) \]

Python实现

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

根据NumPy 的广播功能，如果在标量和NumPy数组之间进行运算，则标量会和NumPy数组的各个元素进行运算。

ReLU函数

ReLU函数可以表示为下面的式:

\[h(x) = \begin{cases} x & \text{ if } x> 0 \\ 0 & \text{ if } x\le 0 \end{cases} \]

Python实现

def relu(x):
    return np.maximum(0, x)

这里使用了NumPy的 maximum函数。 maximum函数会从输入的数值中选择较大的那个值进行输出。

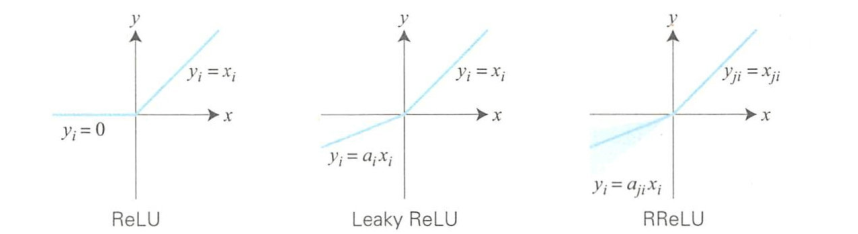
从ReLU衍生的激活函数

ReLU激活函数是一个非线性函数，如果输入小于0则输出0，如果大于等于0则输出该值。
为了在输入小于0时能够输出负值，人们提出了Leaky ReLU、PReLU和 RReLU等激活函数。

这些函数的负数端斜率和正数端的不同。

如LeakyReLU激活函数中，设\(a_i\)是一个很小的值（如1/100 )，则负数端斜率较小。\(a_i\)的值通常都是训练前确定的。

\[y_i = \begin{cases} x_i & \text{ if } x_i\ge 0 \\ \frac{x_i}{a_i} & \text{ if } x_i< 0 \end{cases} \]

而PReLU中的\(a_i\)是在根据误差反向传播算法进行训练时确定的，是从一个均匀分布中随机抽取的数值。
测试时，\(a_i\)使用均匀分布的中央值。通过性能对比测试报告可知，几种函数的实现性能差异不大，不过RReLU的性能最优。

softmax函数

分类问题中使用的softmax函数可以用下面的式表示:

\[y_k= \frac{e^{a_k}}{\sum_{i=1}^{n}e^{a_i}} （e是纳皮尔常数2.7182 . . .） \]

上面式子表示，假设输出层共有n个神经元，计算第k个神经元的输出 \(y_k\)。
softmax函数的分子是输入信号\(a_k\)的指数函数，分母是所有输入信号的指数函数的和。

Python实现

def softmax(a):
	exp_a = np.exp(a)
	sum_exp_a = np.sum(exp_a)
	y = exp_a / sum_exp_a
	
	return y

实现softmax函数时的注意事项:
上面代码，在计算机的运算上有一定的缺陷。这个缺陷就是溢出问题。 softmax函数的实现中要进行指数函数的运算，但是此时指数函数的值很容易变得非常大。
比如， \(e^10\)的值会超过20000， \(e^100\)会变成一个后面有40多个0的超大值， \(e^1000\)的结果会返回一个表示无穷大的inf。
如果在这些超大值之间进行除法运算，结果会出现“不确定”的情况。

改进softmax函数

在分子和分母上都乘上C这个任意的常数（因为同时对分母和分子乘以相同的常数，所以计算结果不变）。
然后，把这个 C 移动到指数函数（exp）中，记为\(logC\)。最后，把\(logC\)替换为另一个符号\(C^{'}\)。

这里的\(C^{'}\)可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值。

\[y_k= \frac{exp(a_k)}{\sum_{i=1}^{n}exp(a_i)} =\frac{C\bullet exp(a_k)}{C \bullet \sum_{i=1}^{n}exp(a_i)}= \frac{exp(a_k+logC)}{\sum_{i=1}^{n}exp(a_i+logC)}= \frac{exp(a_k+C^{'})}{\sum_{i=1}^{n}exp(a_i+C^{'})} \]

对应的Python代码:

def softmax(a):
	c = np.max(a)
	exp_a = np.exp(a - c) # 溢出对策
	sum_exp_a = np.sum(exp_a)
	y = exp_a / sum_exp_a
	
	return y

softmax函数的特征

>>> a = np.array([0.3, 2.9, 4.0])
>>> y = softmax(a)
>>> print(y)
[ 0.01821127 0.24519181 0.73659691]
>>> np.sum(y)
1.0

softmax函数的输出是0.0到1.0之间的实数。并且， softmax函数的输出值的总和是1。输出总和为1是softmax函数的一个重要性质。正因为有了这个性质，我们才可以把softmax函数的输出解释为“概率”。

即便使用了softmax函数，各个元素之间的大小关系也不会改变。
这是因为指数函数（y = exp(x)）是单调递增函数。
因此，神经网络在进行分类时，输出层的softmax函数可以省略。
在实际的问题中，由于指数函数的运算需要一定的计算机运算量，因此输出层的softmax函数一般会被省略。

参考： [1]图解深度学习/(日)山下隆义著;张弥译.--北京:人民邮电出版社，2018.5