线性表
目录
线性表:零个或多个数据元素的有限序列
线性表的顺序存储结构
线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素
注意:
- 任意时刻,线性表的长度应该小于等于数组长度
- 线性表的顺序存储结构,在存、读数据时,不管是哪个位置,时间复杂度都是O(1);而插入或删除,时间复杂度都是O(n)
C语言实现代码
#define MAXSIZE 20 /*存储空间初始分配量*/
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status; /*Status是函数的类型,其值是函数结果状态代码,如ok等*/
typedef int ElemType; /*ElemType 类型*/
/*
*线性表的 【顺序存储结构】
*/
typedef struct
{
ElemType data[MAXSIZE]; /*数组存储数据元素,最大值为MAXSIZE【注意:在任意时刻,线性表的长度应该小于等于数组的长度!】*/
int length; /*线性表当前长度*/
} SqList;
/*
*【1】获得元素操作
*初始条件:顺序线性表 L 已经存在,1≤i≤ListLength(L)
*操作结果:用 e 返回 L 中第 i 个数据元素的值
*
* 解释说明:Status GetElem(SqList L, int i, ElemType *e)
* SqList L :因为取值操作不需要修改原始的线性表,所以传入的是一个副本,可以理解为普通变量
* int i :要获取的元素的下标
* ElemType *e:即 int *e ,之所以是指针类型,是因为一旦GetElem()这个函数执行完,整个函数的变量等信息就会被释放,没法保存
*/
Status GetElem(SqList L, int i, ElemType *e)
{
/*这里是检查空表、要获取元素下标不在范围内的情况*/
if (L.length == 0 || i<1 || i>L.length) /*普通变量,通过 点运算符 操作结构体成员*/
{
return ERROR;
}
*e = L.data[i - 1];
return OK;
}
/*
*【2】插入元素操作
*初始条件:顺序线性表 L 已经存在,1≤i≤ListLength(L)
*操作结果:在 L 中第 i 个位置之前插入新的元素 e , L 的长度加 1
*
* 解释说明:ListInsert(SqList* L, int i, ElemType e)
* SqList* L :因为插入操作是需要修改原始的线性表,所以传入的SqList*指针类型,指针指向原始线性表,这样操作的是原始线性表
* int i :要插入元素在线性表的位置
* ElemType e:即 int e
*/
Status ListInsert(SqList* L, int i, ElemType e)
{
int k;
/*判断 顺序线性表已经满 和 当 i 不在范围的时候*/
if (L->length == MAXSIZE || i<1 || i>L->length+1)
return ERROR;
/*若插入数据位置不在尾表*/
if (i <= L->length) /*指针变量,通过->操作结构体成员*/
{
for (k = L->length - 1; k >= i - 1; k--) /*将要插入位置后数据元素往后移动一位*/
{
L->data[k + 1] = L->data[k];
}
}
L->data[i - 1] = e; /*插入新元素*/
L->length++;
return OK;
}
/*
*【3】删除元素操作
*初始条件:顺序线性表 L 已经存在,1≤i≤ListLength(L)
*操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1
*
* 解释说明:ListDelete(SqList *L, int i, ElemType *e)
* SqList *L :因为插入操作是需要修改原始的线性表,所以传入的SqList*指针类型,指针指向原始线性表,这样操作的是原始线性表
* int i :要删除的元素在线性表的位置
* ElemType *e:即 int *e,保存删除的元素,之所以是指针类型,是因为一旦ListDelete()这个函数执行完,整个函数的变量等信息就会被释放,没法保存
*/
Status ListDelete(SqList *L, int i, ElemType *e)
{
int k;
/*判断 顺序线性表为空 和 当 i 不在范围的时候*/
if (L->length == 0 || i<1 || i>L->length)
return ERROR;
*e = L->data[i - 1]; /*保存要删除的元素*/
if (i < L->length) /*如果删除的不是最后位置*/
{
for (k = i; k < L->length; k++) /*将删除的位置的后继元素前移*/
L->data[k - 1] = L->data[k];
}
L->length--;
return OK;
}
优缺点
优点:
- 无须为表示表中元素之间的逻辑关系而增加额外的存储空间【因为是顺序存储,地址是连续的】
- 可以快速地存取表中任意位置的元素【因为有地址】
缺点:
- 插入和删除操作需要移动大量元素【插入你得给个位置;有空位你得往前走】
- 当线性表长度变化比较大时,难以确定存储空间的容量【存储空间是初始分配好的】
- 造成存储空间的“碎片化”
线性表的链式存储结构
头指针和头结点
头指针:
- 头指针是链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针
- 头指针具有表识作用,所以常用头指针冠以链表名
- 无论链表是否为空,头指针均不能为空。即头指针是链表必要元素
头结点:
- 头结点是为了操作的同意和方便而设立的,放在第一元素的结点之前,其数据域一般无意义(也可以存放链表长度)
- 头结点不一定是链表必须的
带头节点的单链表判空:看head->next是否为NULL;
不带头结点的单链表判空:看头指针head是否为NULL。
C语言实现
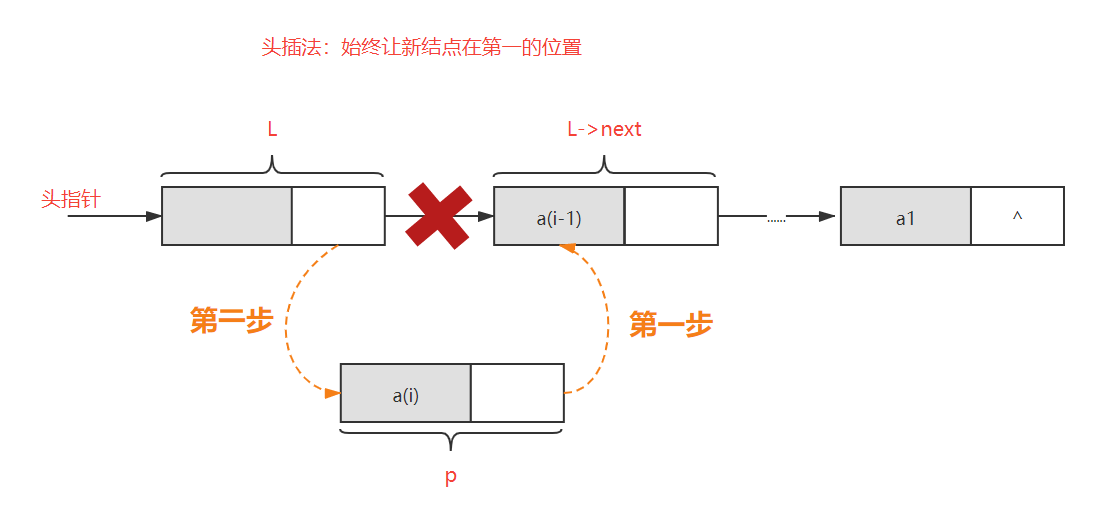
创建单链表【头插法】图解:
/*
*【0】单链表创建【头插法】
*操作结果:建立带头结点的单链表L(头插法)
*/
void CreateListHead(LinkList* L, int n)
{
LinkList p;
int i;
srand(time(0)); /*初始化随机种子*/
/*先建立一个带头结点的单链表*/
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL;
for (i = 0; i < n; i++)
{
/*创建结点并赋值*/
p = (LinkList)malloc(sizeof(Node));
p->data = rand() % 100 + 1;
p->next = (*L)->next;
(*L)->next = p;
}
}
sizeof()是运算符,不是函数!
创建单链表【尾插法】图解:
/*
*【0】单链表创建【尾插法】
*操作结果:建立带头结点的单链表L(尾插法)
*/
void CreateListHead(LinkList* L, int n)
{
LinkList p,r;
int i;
srand(time(0)); /*初始化随机种子*/
/*先建立一个带头结点的单链表*/
*L = (LinkList)malloc(sizeof(Node));
r = *L;
for (i = 0; i < n; i++)
{
/*创建结点并赋值*/
p = (Node*)malloc(sizeof(Node));
p->data = rand() % 100 + 1;
r->next = p;
r = p;
}
r->next = NULL;
}
读取操作图解:
#include <stdlib.h>
#define MAXSIZE 20 /*存储空间初始分配量*/
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status; /*Status是函数的类型,其值是函数结果状态代码,如ok等*/
typedef int ElemType; /*ElemType 类型*/
/*
*线性表的 【链式存储结构】
*/
typedef struct Node
{
ElemType data;
struct Node *next;
} Node;
typedef struct Node* LinkList; /*定义LinkList*/
/*
*【1】读取元素操作
*初始条件:顺序线性表 L 已经存在,1≤i≤ListLength(L)
*操作结果:用 e 返回 L 中第 i 个数据元素的值
*
* 解释说明:Status GetElem(LinkList L, int i, ElemType *e)
* LinkList L :因为取值操作不需要修改原始的线性表,所以传入的是一个副本,可以理解为普通变量
* int i :要获取的元素的下标
* ElemType *e:即 int *e ,之所以是指针类型,是因为一旦GetElem()这个函数执行完,整个函数的变量等信息就会被释放,没法保存
*/
Status GetElem(LinkList L, int i, ElemType* e)
{
int j;
LinkList p; /*声明一指针p*/
p = L->next; /*让指针p指向链表L的第一个结点*/
j = 1; /*j为计数器*/
while (p && j<i) /* 指针p 不为空,且计数器 j 还没有等于 i 时,循环继续*/
{
p = p->next; /*让 p 指向下一个结点*/
++j;
}
if (!p || j > i) /*第i个结点不存在*/
return ERROR;
*e = p->data; /*取第i个结点的数据*/
return OK;
}
插入操作图解:
/*
*【2】插入元素操作
*初始条件:顺序线性表 L 已经存在,1≤i≤ListLength(L)
*操作结果:在 L 中第 i 个位置之前插入新的元素 e
*
* 解释说明:ListInsert(LinkList *L, int i, ElemType e)
* SqList* L :因为插入操作是需要修改原始的线性表,所以传入的LinkList*指针类型,指针指向原始线性表,这样操作的是原始线性表
* int i :要插入元素在线性表的位置
* ElemType e:即 int e
*/
Status ListInsert(LinkList* L, int i, ElemType e)
{
int j;
LinkList p, s;
p = *L;
j = 1;
while (p&&j<i) /*寻找第i-1个结点*/
{
p = p->next;
++j;
}
if (!p || j > i)
return ERROR; /*不存在第i-1个结点*/
s = (LinkList)malloc(sizeof(Node)); /*生成新结点*/
s->data = e;
s->next = p->next; /*将p的后继结点赋值给s的后继结点*/
p->next = s; /*将s赋值给p的后继*/
return OK;
}
删除结点操作图解:
/*
*【3】删除元素操作
*初始条件:顺序线性表 L 已经存在,1≤i≤ListLength(L)
*操作结果:删除L的第i个数据元素,并用e返回其值
*
* 解释说明:ListDelete(LinkList *L, int i, ElemType *e)
* LinkList *L :因为插入操作是需要修改原始的线性表,所以传入的LinkList*指针类型,指针指向原始线性表,这样操作的是原始线性表
* int i :要删除的元素在线性表的位置
* ElemType *e:即 int *e,保存删除的元素,之所以是指针类型,是因为一旦ListDelete()这个函数执行完,整个函数的变量等信息就会被释放,没法保存
*/
Status ListDelete(LinkList* L, int i, ElemType* e)
{
int j;
LinkList p,q;
p = *L;
j = 1;
while (p->next && j < i) /*寻找第i-1个结点*/
{
p = p->next;
++j;
}
if (!(p->next) || j > i)
return ERROR; /*不存在第i-1个结点*/
q = p->next;
p->next = q->next; /*将q结点的后继赋值给p的后继*/
*e = q->data; /*将p结点中的数据给e*/
free(q); /*让系统回收此结点,释放内存*/
return OK;
}
删除链表操作图解:
/*
*【4】单链表删除
*操作结果:将L重置为空表
*/
Status ClearList(LinkList* L)
{
LinkList p, q;
p = (*L)->next;
while (p)
{
q = p->next;
free(p);
p = q;
}
(*L)->next = NULL;
return OK;
}
单链表结构与顺序存储结构优缺点
存储分配方式:
- 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素
- 单链表采用链式存储结构,用一组任意的存储单元存放线性表的元素
时间性能:
| 查找 | 插入和删除 | |
|---|---|---|
| 顺序存储结构 | O(1) | O(n) |
| 单链表 | O(n) | O(1) |
空间性能:
- 顺序存储结构需要预分配存储空间,分大了,浪费;分少了,溢出;且容易造成“空间碎片”
- 单链表不需要分配存储空间,只要有空间,就可以分配,元素个数也不受限制
循环链表
将单链表中终端结点的指针端由空指针改为指向头结点,就使得整个单链表形成一个环,这种头尾相接的单链表称为 单循环链表
两个单循环链表合并图解:
p = rearA->next;
rearA->next = rearB->next->next;
q = rearB->next;
rearB->next = p;
free(q);
双向链表
双向链表实在单链表的每个结点中,再设置一个指向其前驱结点的指针域
插入操作图解:
s->prior = p;
s->next = p->next;
p->next->prior = s;
p->next = s;
删除操作图解:
p->prior->next = p->next;
p->next->prior = p->prior;
free(p);
参考:
[1]大话数据结构/程杰著.——北京:清华大学出版社,2011.6











 浙公网安备 33010602011771号
浙公网安备 33010602011771号