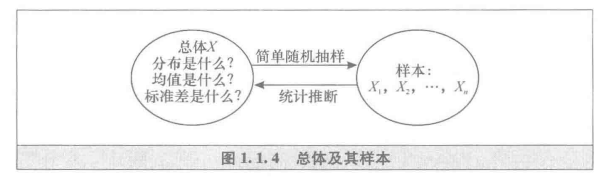
总体和样本
总体和分布
在一个统计问题中,我们把研究对象的全体称为总体,其中每个成员称为个体。
比如:
研究学龄前儿童这个总体,每个儿童就是一个个体,
每个个体都有很多侧面,如身高、体重、血色素、性别等。
若我们进一步明确:研究对象是儿童的血色素(X)的大小,这样一来每个个体(儿童)对应一个数。如果撤开实际背景,那么总体就是一堆数,这堆数中有的出现的机会大,有的出现的机会小,因此可以用一个概率分布来描述这个总体。
从这个意义上讲,总体就是一个分布,其数量指标X就是服从这个分布的随机变量。因此,常常用随机变量的符号或分布的符号表示总体。比如我们说“从某总体中抽样”和“从某分布中抽样”是同一个意思。
总体还可以按个体数量分为有限总体和无限总体。
现实世界中大部分是有限总体。当个体个数很多以致不易数清时就把该总体看做无限总体。
有限总体将是抽样调查和抽样检验的研究对象。
样本
样本、样品、样本量(样本容量)
研究总体分布及其特征数有如下两种方法:
-
(1)普查
又称全数检查,即对总体中每个个体都进行检查或观察。- 因普查费用高、时间长,不常使用,破坏性检查(如灯泡寿命试验)更不会使用。
- 只有在少数重要场合才会使用普查。
- 如我国规定每十年进行一次人口普查,期间九年中每年进行一次人口抽样调查。
-
(2)抽样
即从总体抽取若干个体进行检查或观察,用所获得的数据对总体进行统计推断。
- 由于抽样费用低、时间短,实际使用频繁。
- 没有抽样就没有统计学。
从总体中抽出的部分(多数场合是小部分)个体组成的集合称为样本
样本中所含的个体称为样品
样本中样品个数称为样本量或样本容量
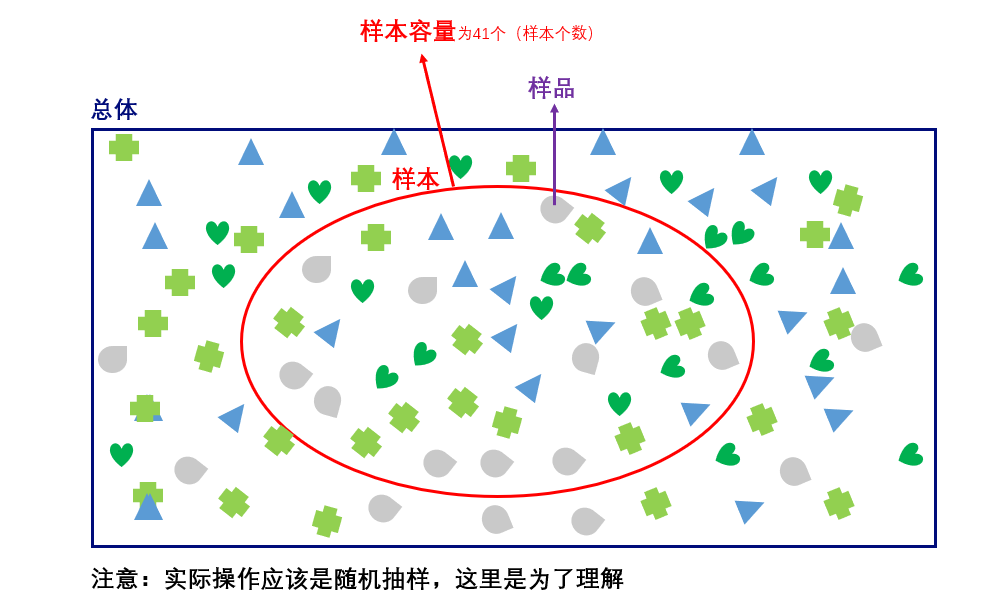
由于抽样前不知道哪个个体被抽中,也不知道被抽中的个体的测量或试验结果,所以容量为 n 的样本可看做 n 维随机变量,用大写字母表示容量为 n 的样本
用小写字母表示其观察值,这就是我们常说的数据
一切可能观察值的全体 \(\chi =\left \{ \left ( x_1,x_2,…,x_n \right ) \right \}\) 称为n维样本空间。
有时为了方便起见,不区分大小写,样本及其观察值都用小写字母\(x_1,x_2,…,x_n\)表示。当需要区分时会加以说明,也可从上下文中识别。
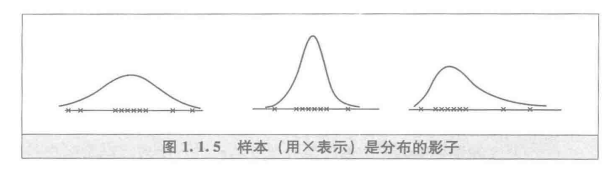
样本来自总体,样本必含总体信息。
机会大的(概率密度值大的)地方被抽中的样品就多,而机会小的(概率密度值小的)地方被抽中的样品就少;
分布分散,样本也分散;分布集中,样本也相对集中;分布有偏,样本中多数样品也偏向一侧等。
样本是分布的影子,见下图。
抽样方法
为了使所抽取的样本能很好地反映总体,抽样方法的确定很重要。
最理想的抽样方法是简单随机抽样,它满足如下两个要求:
-
(1)随机性:即要求总体中每个个体都有同等的机会被选到样本中。说明样本中每个 \(X_i\) 的分布相同,均与总体 \(X\) 同分布。
-
(2)独立性:样本中每个个体的选取并不影响其他个体的选取。这意味着样本中每个个体 \(X_i\) 是相互独立的。
由简单随机抽样得到的样本称为简单随机样本,简称样本。
此时 \((X_1,X_2,…,X_n)\) 可以看成是相互独立且服从同一分布的随机变量,简称独立同分布样本。
如何才能获得简单随机样本呢? 下面例子中介绍的几种方法可供参考。
有一批灯泡600只,现要从中抽取6只做寿命试验,如何从600只灯泡中抽取这6只灯泡,使所得样本为简单随机样本?
-
方案一:设计一个随机试验
先对这批灯泡从 000 ~ 599 编号。然后在600张纸质与大小相同的纸片上依次写上 000 ~ 599,并把它们投入一个不透明的袋中,充分搅乱。最后不返回地抽出6张纸片,其上6个样本号(462,078,519,312,167,103)所组成的样本就是简单随机样本。 -
方案二:利用随机数表
用一大本随机数表中的一页(一般教材后面就有)。我们可以从该表任意位置开始读数。仍把灯泡编号 000 ~ 599,设从该表的第一行第一列开始,以三列为一个数,从上到下读出:537,633,358,634,982,026,645,850,585,358,039,626,084,...凡其值大于600的便跳过,如出现的数与前面重复也跳过,直到选出6个不超过600的不同数为止。现可将编号为537,358,026,585,039,084的6只灯泡取出测定其寿命。 -
方案三:可利用计算机产生6个 000 ~ 599 间的不同的随机整数
譬如产生的随机整数为80,568,341,107,57,166。取出这些编号所对应的灯泡进行试验,测定其寿命。 -
方案四:用扑克牌设计一个随机试验
从一副扑克牌中剔去大小王及K,Q,J各四张,余下40张牌不分花色都当数字用,其中A代表1,10代表0,其他数字直接引用。在这些准备下,可从40张牌中进行有放回地抽取3张。每次抽取前洗牌要充分,抽取要随机。约定第一张牌上的数字为个位数,第二张牌上的数字为十位数,第三张牌上的数字为百位数。若第三张牌上的数字为6~9,则作废重抽,直到第三张牌上的数字不超过5为止。如此得到的三位数(如239)就是第一个样本号,这样重复5次,取得6个样本号(如239,582,073,503,145,366),选择对应编号的样品进行寿命试验。
这里介绍的多种抽样方法说明简单随机样本并不难获得,困难在于排除“人为干扰”,不要“怕麻烦”和“想偷懒”。很多事例表明,统计推断常在抽样阶段出问题。
从样本认识总体的图表方法
样本含有总体信息,但样本中的数据常显得杂乱无章,需要对样本进行整理和加工才能显示隐藏在数据背后的规律。
对样本进行整理与加工的方法有图表法和构造统计量。
这里将介绍几种常用的图表法,如频数频率表和直方图。
频数频率表
当样本量 n 较大时,把样本整理为分组样本可得频数频率表,它可按观察值大小显示出样本中数据的分布状况。
下面通过一个例子来详述整理过程:
光通量是灯泡亮度的质量特征。现有一批220伏25瓦白炽灯泡要测其光通量的分布,为此从中随机抽取120只,测得其光通量如表1.1.5所示。
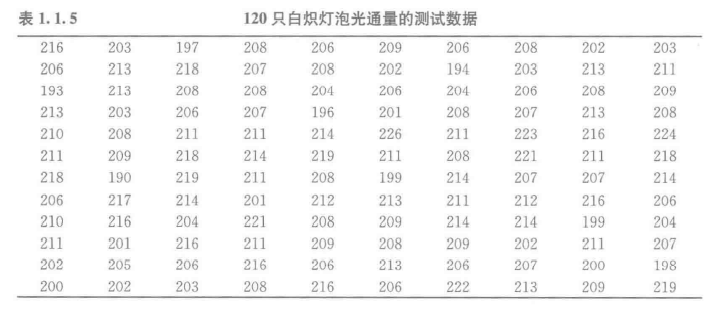
为从这组数据中挖掘出有用信息,常对数据进行分组,获得频数频率表,即分组样本,具体操作如下:
(1)找出这组数据的最大值 \(x_{max}\) 与最小值 \(x_{min}\),计算其差:
R 称为极差,也就是这组数据所在的范围。
在本例中 \(x_{max}\) = 226,\(x_{min}\) = 190,其极差为 R = 226 — 190 = 36。
(2)根据样本量 n 确定组数 k 。
经验表明,组数不宜过多,一般以5~20组较为适宜。可按表1.1.6选择组数。

在本例中,n=120,拟分13组。
(3)确定各组端点 \(a_o < a_1 < …< a_x\),通常 \(a_o < x_{min}\),\(a_k > x_{max}\)。
分组可以等间隔,也可以不等间隔,但等间隔用得较多。
在等间隔分组时,组距 \(d \approx\frac{R}{k}\) 。
在本例中,取 \(a_0 = 189.5,d=36/13\approx3\) ,则有
(4)用唱票法统计落在每个区间 \((a_{i-1},a_i](i=1,2,… ,k)\) 中的频数 \(n_i\) 与频率 \(f_i = n_i/n\)。
把它们按序归在一张表上就得到了频数频率表,见表1.1.7。
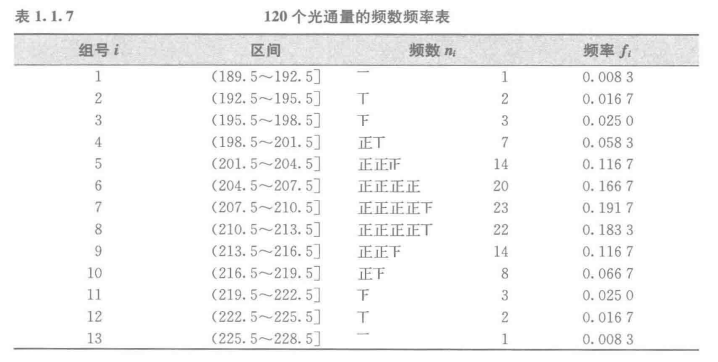
从该表可以看出样本中的数据在每个小区间上的频数 \(n_i\) 与频率 \(f_i\) 的分布状态。
大部分数据集中在 209 附近,201.5 ~ 216.5间含有 77.5% 的数据。
为了使这些信息直观地表示出来,可在频数频率表的基础上画出直方图。
直方图
根据上面的频数频率表可以得出,如下直方图:
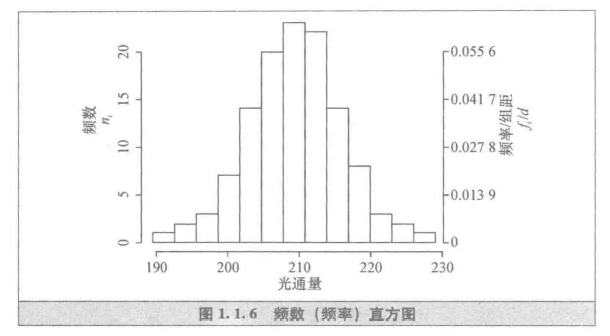
在样本量较大的场合,直方图常是总体分布的影子。
如图1.1.6上的直方图中间高,两边低,左右基本对称。这很可能是“白炽灯泡光通量常是正态分布”的影子。
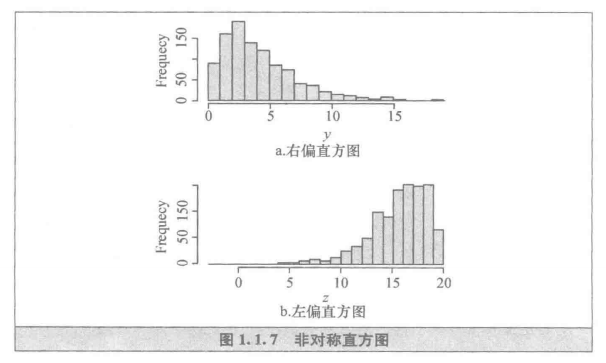
又如图1.1.7上的两个直方图是不对称的,是有偏的,其相应的总体可能是偏态的。
其中一个是右偏分布(见图1.1.7a);另一个是左偏分布(见图1.1.7b)。
直方图的优点
直方图的优点是能把样本中的数据用图形表示出来。
直方图的缺点
直方图的缺点是不稳定,它依赖于分组,不同分组可能会得出不同的直方图。所以从直方图上可得总体分布的直观印象,但认定总体分布还需用其他统计方法。
参考:
[1]数理统计学(2版)/茆诗松等编著.北京:中国人民大学出版社,2016.1


 浙公网安备 33010602011771号
浙公网安备 33010602011771号