社区发现与评价
以结点为中心(node-centric)的社区发现
基于结点中心标准的社区发现方法要求一个团体中的每一个结点都要具备一定的属性。
完全的相互关系
一个理想的内聚子群是一个团(clique),它是一个最大的完全子图,其中所有的结点都是相互连接的。
比如,在下图所示的网络中,有一个4个结点的团,即{5,6, 7, 8}。一般来说,团的规模越大越有意义,但搜索图中的最大团(maximum clique)是一个NP难问题。
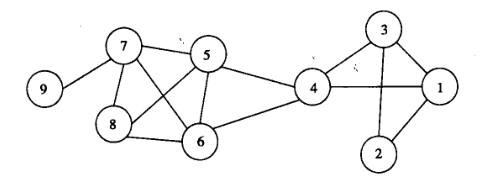
蛮力( brute-force)搜索算法
蛮力( brute-force)搜索算法就是浏览一个网络的所有结点。对于每个结点,检查是否存在包含那个结点的团。
假设考虑结点 $ v_i$ ,可以保存一个由团组成的队列。这个队列的初始值是只有一个结点的团{$ v_i$},然后执行以下操作:
- 从队列中取出一个团,假定它是规模为 k 的一个团 \(B_k\), 令 $ v_i$ 表示最后加入团 \(B_k\) 的结点。
- 对于 $ v_i$ 的每一个邻居 $ v_j$ ,(为了避免重复,只考虑那些下标比 i 大的结点)得到一个新的候选集\(B_{k+1} = B_k ∪ \left \{ v_j \right \}\)。
- 通过检验结点 $ v_j$ 是否与 \(B_k\) 的所有结点相邻来验证 \(B_{k+1}\) 是否是一个团。如果 \(B_{k+1}\) 是一个团,则将它加入队列。
以下图的网络为例:

假设从 结点4 开始,\(B_1\)= {4}。
对于 结点4 的每一个下标比它大的邻居,就得到两个规模为 2 的团:{4,5} 和 {4,6},然后将其加人队列。
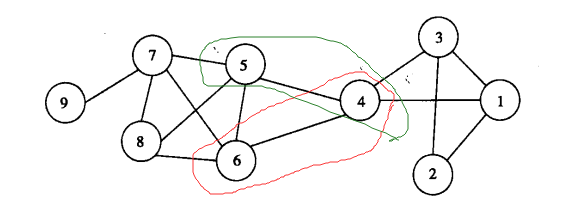
假设将团 \(B_2\) = {4,5} 从队列中取出,那么最后加入的元素是结点 5 。
可以根据 结点5 的邻居扩展这个集合,得到3个候选集:{4,5,6}、{4,5,7}和 {4,5,8}。
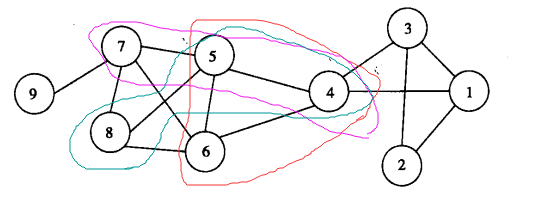
但只有 {4,5,6 }是一个团,因为结点6既与结点4连接,又与结点5连接。
这样,将 {4,5,6}加入到队列以便进一步搜索更大的团。
以上的穷举搜索只能适用于小规模网络,对于大规模网络它是无能为力的。
如果想要发现一个最大团,那么一个策略就是有效的剪枝策略:
剪去那些不太可能包含在团中的结点和边。
对于一个规模为 k 的团,其中每个结点的度最少为 k-1。
因此,那些度小于 k-1 的结点不可能包含在最大团中,这样就可以达到剪枝的目的。
假设从下图的网络中随机取样得到一个子网,它包含从结点1到结点6的6个结点。

这个子网的最大团的规模为3,即{1,2,3}或{1,3,4}。如果在原来的网络中包含一个更大的团,比如规模大于3,那么所有度小于或等于2的结点都可以删除,不用考虑。因此,结点9和结点⒉就被剪枝。之后,结点1和结点3的度就降为2,因此,它们也被删除。删除结点1和结点3后,就进一步导致结点4的度也只有2,因此它也被删除。经过这些剪枝后,就可以得到一个小得多的网络:{5,6,7,8}。在这个剪枝后的网络中,规模为4的团就可以直接识别,它就是最大的团。
团是一个非常严格的定义。在现实的社会网络中,很少能够观察到大规模的团。团的结构是非常不稳定的,因为删除其中的任意一条边就会导致这个团被破坏。实际中被识别的团一般当做种子(seed)或核心(core),然后再做相应的扩展形成社区。
团过滤算法( Clique Percolation Method , CMP)
团过滤算法( Clique Percolation Method , CMP)就属于这种方法,可以用来分析具有重叠性的社区结构( Palla et al , 2005)。
给定一个用户指定的参数 k,其工作过程如下:
- 在给定网络中找出所有规模为 k 的团。
- 构建一个团图,如果两个团共享 k-1 个结点,那么它们是邻接的。
- 在团所构成的图(clique graph)中,每一个连接的部分(component)就是一个社区。
以下图的网络为例,

比如k=3,可以识别下列所有规模为3的团:
{1,2,3}、{1,3,4}、{4,5,6}、 {5,6,7} 、{5,6,8} 、{5,7,8}、{6,7,8} 然后就得到如下图所示的团图。
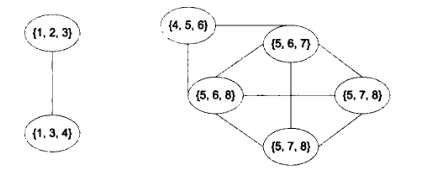
只要两个团共享k-1个结点,在这个例子中共享2个结点,那么它们就被连接起来。
每个被连接起来的团的结点都属于同一个社区。
因此,就可以得到两个社区,即{1,2,3,4}和{4,5,6,7,8}。
其中结点4属于两个社区,也就是说得到了两个重叠的社区。
以群为中心(group-centric)的社区发现
以网络为中心(network-centric)的社区发现
结构性等价(structural equivalence)
如果用户 \(v_i\) 与 \(v_j\) 是结构性等价的,那么它们都与网络的同一个用户集合相连接。
如果将它们的交互表示为一个矩阵,那么 \(v_i\) 与 \(v_j\) 的行(列) 除了对角元素外都是一样的。

在上图中,结点1和结点3就是结构性等价的,结点5和结点6也是结构性等价的。
从下表的邻接矩阵中可以看到,那些结构性等价的结点的行和列具有相同的值(除了对角元素)。
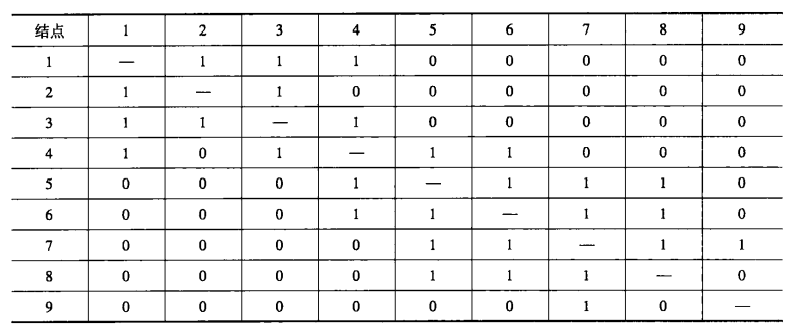
属于相同等价类的结点形成一个社区。
Jaccard相似性与Cosine相似性
其中,\(N_i\)表示结点 \(v_i\) 的邻域, | * |表示集合的势,即元素的个数,相似性度量的取值范围都在0~1之间。
例如:

\(N_4\) = { 1,3,5,6},\(N_6\) = {4,5,7,8},那么这两个结点(4和6)之间的相似性为:
然而,根据这种定义,两个相邻的结点之间的相似性可能为0。
比如,结点7与结点9,即使它们相连,它们的相似性也为0。因为\(N_7\)={5,6,8,9},\(N_9\)={7},所以 \(N_7\cap N_9 = ∅\)。
从结构性等价的观点来看,这是合理的。但是,从相互关系的角度来说,如果两个结点相连,它们很可能具有相似性。
一种修正方法就是在计算\(N_v\)时,包含结点 v 。也就是说,将一个网络的邻接矩阵的对角元素设置为1,而不是缺省值0。
在这种情况下,\(N_7\)={5,6,7, 8,9},\(N_9\)={7, 9},那么 \(N_7\cap N_9\) = {7,9}:
标准的基于相似性的方法需要计算每一对结点的相似性,时间复杂度为O(\(n^2\))。
多维量表算法(Multi-Dimen-sional Scaling,MDS)
多维量表算法( Multi-Dimen-sional Scaling,MDS) ( Borg and Groenen,2005)。
一般来说,MDS需要输人一个相似矩阵( proximity matrix ) P ∈ \(R_{nxn}\),其中元素 P,表示网络中结点i和j之间的距离。
令 S ∈ R,表示结点在 \(l\) 维空间的坐标,并使得 S 的列是正交的,那么就可以观察到以下公式( Borg and Groenen,2005 ;Sarkar and Moore,2005) :
其中 \(Ⅰ\) 表示单位矩阵,\(1\) 每个元素都是 1 的一个n维列向量,而 \(\circ\) 表示矩阵按元素进行相乘。
\(S\) 可通过以下的公式获得,使得 \(\tilde{P}\) 与 \(SS^T\) 的差最小:
假设 \(V\) 包含 \(\tilde{P}\) 中的 \(l\) 个最大特征值的所对应的特征向量,\(Λ\) 是 \(l\) 个特征值组成的对角矩阵, \(Λ\) = diag \((入_1,入_2,…,入_l)\),则 \(S\) 的最优值就是 S = \(VΛ^{\frac{1}{2}}\) 。
注意,这种多维量表算法对应一个矩阵的特征向量问题。因此,传统的 K 均值算法可以用来实施社区划分。
以下图的网络为例:

给定一个网络后,结点之间的距离就可以通过一个近似矩阵 P 来刻画。
然后根据式\(SS^T=\tilde{P}\)就可以计算 \(\tilde{P}\):

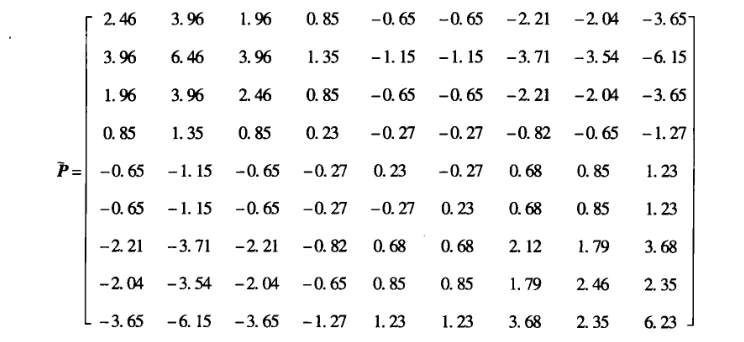
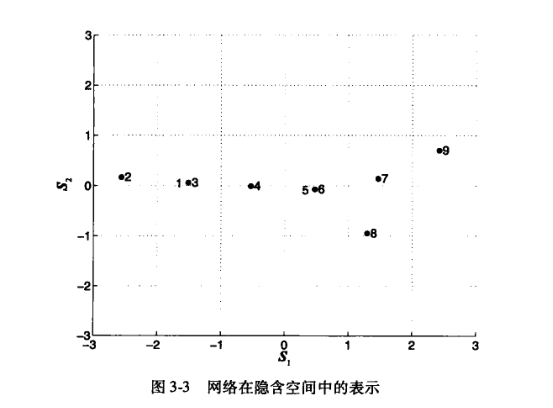
假设希望将原来的网络映射到一个2维的空间,通过计算,获得以下的\(V、Λ和S\):

由于结点1和结点3在结构上是等价的,它们在隐含空间( latent space)中被映射为同一个点。结点5和结点6也是一样。
为了获得网络的不相交划分,对 S 应用 k均值算法 进行运算。最后,获得了两个聚类{1,2,3,4}和{5,6,7,8,9},这可以表示为以下的划分矩阵H:
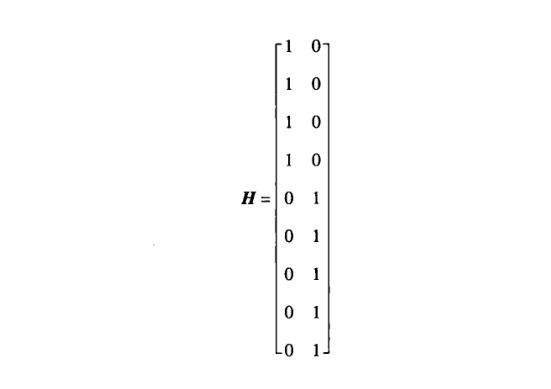
块模型近似
块模型近似方法是通过块模型来近似刻画块的结构。从下面两个表可以看出这个方法的思想。

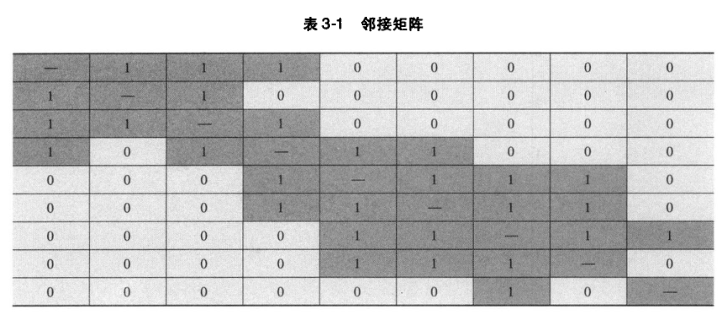
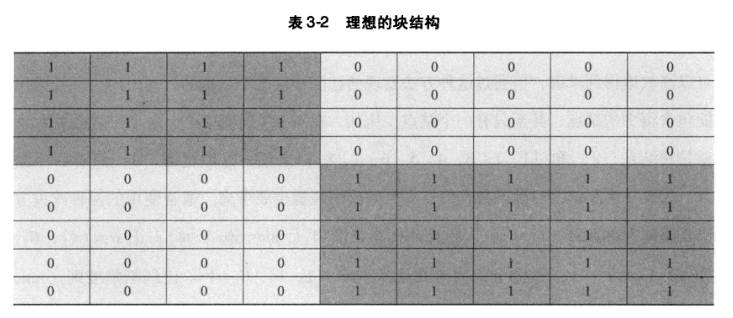
表3-1描述了图的邻接矩阵,通过彩色阴影突出那些表示两个结点之间相连的元素。
以层次结构为中心( hierarehy-cen-tric)的社区发现
参考:
[1] (美)唐磊( Lei Tang)等著;文益民,闭应洲译.社会计算:社区发现和社会媒体挖掘[M].机械工业出版社:北京,2012


 浙公网安备 33010602011771号
浙公网安备 33010602011771号