线性阈值模型( Linear Threshold Model) - 独立级联模型(Independent Cascade Model)
线性阈值模型(Linear Threshold Model)
阈值（threshold）模型的研究可以回溯到1970年 ( Granovetter，1978)。
该模型表明：如果一个用户的采取行动的朋友的数量超过某个阈值，那么该用户才采取行动。
在线性阈值模型(Linear Threshold Model，LTM)中，每个结点 V 在0~1内均匀分布随机抽取一个阈值 \(Θ_v\) 。
阈值 \(Θ_v\) 表示为了激活结点V，结点 V 的朋友需要被激活的比例。
假定该网络为有向网，也就是说权值 \(b_{w,v}\) 和 \(b_{v,w}\) , 在线性阈值模型中将起着不同的作用。
为简单起见，假定 \(b_{w,v}\) = 1/\(k_v\)， \(b_{v,w}\) = 1/\(k_w\)，每个结点的阈值设为0.5。
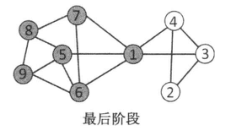
假设最初的活动结点是结点8和结点9。下图描述了在线性阈值模型条件下信息扩散的过程。
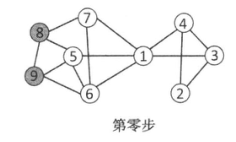
在这个过程的第一步，结点5由于其两个邻接结点处于活动状态，并且指向结点5的权值 \(b_{8,5}\) + \(b_{9,5}\)= 1/3 +1/3 =2/3，2/3大于阈值0.5，所以结点5被激活。
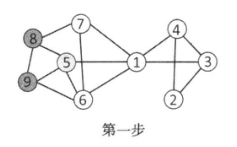
在第二步中，由于结点6的两个邻接结点5和结点9处于活动状态，因此结点6被激活。
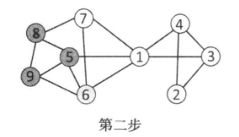
从而有结点7和结点1在第三步中被激活。
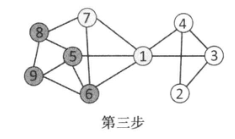
当结点1、5、6、7、8、9被激活后，网络中剩余的其他结点都达不到被激活的条件，因此当结点1、5、6、7、8、9被激活后，信息扩散过程就停止。
独立级联模型(Independent Cascade Model)
独立级联模型( Independent Cascade Model，ICM）借鉴了交互粒子系统（ interac-ting particle)和概率论的理念。
与线性阈值模型不同，该模型关注信息的发送者( sender）胜过信息的接收者（receiver)。
在独立级联模型中，一个 结点w 一旦在 第t步 被激活，它只有一次机会激活它的邻接结点。
对于其 邻接结点v ，其被 结点w 激活的概率为 \(P_{w,v}\)。
如果 v 被成功地激活，那么 v 就是 第 t+1 步 被激活的结点。
在往后的信息扩散过程中, w 将不再试图去激活它其余的邻接结点。
在独立级联模型中，信息扩散过程与线性阈值模型的信息扩散过程相同，都从一个初始活动的结点集合开始，直到没有结点可以被激活而结束。
举例：
假定网络中的所有结点对都有 \(P_{w,v}\)=0.5，也就是说，一个结点一旦被激活，它将以50%的概率激活它的邻接结点。
设结点8和结点9为初始活动的结点。
从 结点8 和 结点9 开始，独立级联模型根据 \(P_{w,v}\)=0.5 的值激活它们的邻接结点。
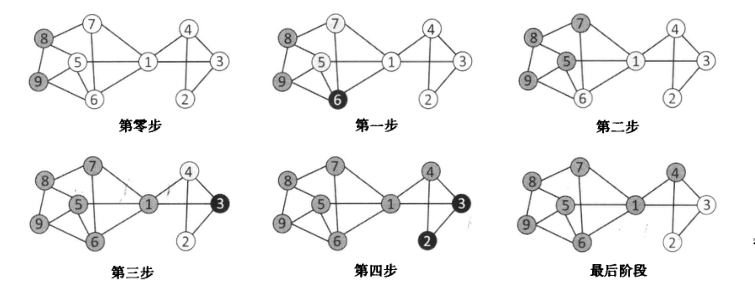
在第一步中，结点8 和 结点9 试图激活它们的邻接结点 5、6 和 7 。假设只有 结点5 和 结点7 被成功地激活，结点6 的激活失败;
给定活动结点5和7，继续按照 \(P_{w,v}\)=0.5 的概率激活它们邻接结点。
第二步中，假设 结点1 和 6 被成功激活。
由于 结点6 的所有邻接结点都已被激活，所以在第三步中只要考虑 结点1的邻接结点。
按照独立级联模型，结点3 和 结点4 将以50%的概率被激活。假设只有结点4被成功激活。
在第四步中，考虑最近被激活的 结点4 的邻接结点。假设 结点4 的邻接结点没有一个被成功激活。
那么，网络中信息扩散过程到结点1、4、5、6、7、8、9被激活就终止了。
注意，独立级联模型以一定的概率激活一个结点，因此，网络中的结点被激活的顺序并不唯一。
遵守独立级联模型的信息扩散过程。深灰色表示结点是活动的，浅灰色表示结点最近被激活，黑色表示结点激活失败
对比
线性阈值模型和独立级联模型在一定程度上体现了信息扩散的特点（Cruhl et al. , 2004)，
两个模型都引入了随机性，线性阈值模型算法在信息扩散启动之前为结点随机地选择阈值，而独立级联模型中一个结点以概率 \(P_{w,v}\)去激活其邻接结点。
但是两者又有明显的不同。
线性阈值模型
- 以接收者为中心(receiver-centered)，通过观察一个结点的所有邻接结点，根据该结点的阈值决定是否可以激活该结点;
- 结点的激活依赖于一个结点的全部邻接结点;
- 一旦给定线性阈值模型中的阈值，网络中的信息扩散过程也就确定了。
独立级联模型
- 以发送者为中心（ sender-cen-tered)。当一个结点被激活后，它试图去激活它的所有邻接结点；
- 一个结点独立地激活其所有的邻接结点（不一定都被激活)；
- 信息扩散的过程随信息的级联过程（ cascading process）而变。网络中的信息扩散过程不确定了。
参考：
[1] (美）唐磊（ Lei Tang）等著;文益民,闭应洲译.社会计算:社区发现和社会媒体挖掘[M].机械工业出版社:北京,2012
