“桥”（bridge）- 邻域重叠度( neighborhood overlap)
“桥”（bridge）
如果网络中的一条边删除后，会导致这条边的两个端结点不再连接，则这条边称为“桥”。
称为桥的边在网络中属于弱联系。
例如，在下图中，边 e(2，5）就是这样一条属于弱联系的边。
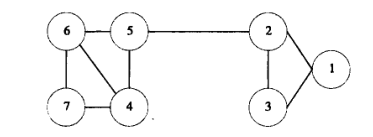
如果将该边移除，结点2和结点5将不再有边相连接。
但是，在现实世界网络中，像 e(2，5）这样的边是不常见的。
通常的情况是：当两个结点之间的某条边移除后，这两个结点仍然通过其他的边相连接。
如下图所示，如果移除边e(2，5）后，结点2和结点5仍然通过结点8、9、10相连接。
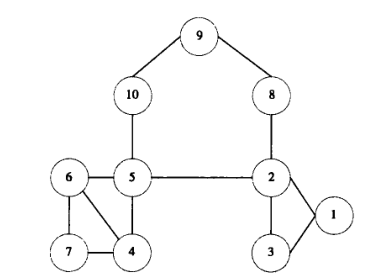
因此，一个联系的强度可以通过计算当直接连接两个结点的边移除后，剩余的连接这两个结点的其他路径的最短长度得到。
如果两个结点间没有边相连，那么这两个结点之间的最短距离就是 +∞。
当两个结点之间的直接连接的边移除后，这两个结点之间的最短距离越大，被移除的边的强度就越小。
以下图所示的网络为例，
当把边e(2，5）移除后，结点⒉和结点5之间的最短距离d(2,5)=4。
同样，可以知道当边e(5，6)移除后，结点5和结点6之间的最短距离d(5,6)=2。
因此，可以认为边e(5，6）比边e(2，5)要强。
邻域重叠度( neighborhood overlap)
另外一种计算联系强度的方法是基于两个结点的邻域重叠度（ neighborhood overlap)( Onnela et al. , 2007; Easley and Kleinberg，2010)。
设 \(N_i\) 表示结点 \(v_i\) 的朋友的集合，给定链接 \(e( v_v，v_j)\)，两个结点的邻域结点的重合程度可以计算如下:
在上式的分母中之所以有-2，就是为了将结点\(v_i\)和结点\(v_j\)从集合 \(|N_i∪N_j|\) 中排除。
通常，两个结点的邻域重叠度越大，这两个结点之间的联系就越强。
据报道两个人朋友的重合程度与两个人在通信网络里联络的时间成正比 （ Onnela，et al. , 2007)。
在下图中，
\(N_2\) = {1，3，5，8}
\(N_5\) = {2，4，6，10}。
由于\(|N_2 ∩ N_5 |\)= 0 ，所以结点⒉和结点5的邻域重叠度overlap(2,5)=0，这说明了这两个结点之间的联系较弱。
相反，结点5和结点6的邻域重叠度为:
因此，边e(5，6)比边e(2，5）表示的联系更强。
参考：
[1] (美）唐磊（ Lei Tang）等著;文益民,闭应洲译.社会计算:社区发现和社会媒体挖掘[M].机械工业出版社:北京,2012
