平均路径长度与直径

目录

• 无权无向网络情形
  • 平均路径长度
    • 最短路径(Shortest path)与测地路径(Geodesic path)
    • 平均路径长度( Average path length)
  • 网络直径(Diameter)
• 加权有向网络情形

---

返回 我的研究方向(Research Interests)

---

无权无向网络情形

平均路径长度

最短路径(Shortest path)与测地路径(Geodesic path)

网络中两个节点 i 和 j 之间的最短路径(Shortest path)也称为测地路径(Geodesic path)，是指连接这两个节点的边数最少的路径。

节点 i 和 j 之间的距离 d ，定义为连接这两个节点的最短路径上的边的数目，也称为两个节点之间的测地距离(Geodesic distance)或跳跃距离(Hop distance)。

平均路径长度( Average path length)

网络的平均路径长度( Average path length) L 定义为任意两个节点之间的距离的平均值，网络的平均路径长度也称为网络的特征路径长度( Characteristic path length)或平均距离(Average distance)。即

\[L= \frac{1}{\frac{1}{2}N(N-1) }\sum_{i\ge j}^{}d_{ij} \]

其中N为网络节点数。
对于下图所示的一个包含5个节点和5条边的简单网络

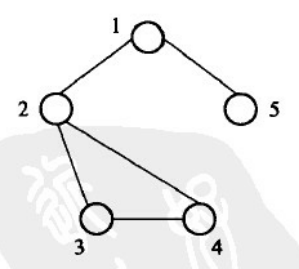
有L=1.7。
在朋友关系网络中，平均路径长度L是连接网络内两个人之间最短关系链中的朋友的平均个数。
尽管许多实际的复杂网络的节点数巨大，网络的平均路径长度却小得惊人，这就是所谓的小世界现象。

大型实际网络往往是不连通的
此时，可能两个节点之间不存在连通的路径，即意味着这两个节点之间的距离为无穷大，从而导致整个网络的平均路径长度也为无穷大。
为了避免在计算时出现这种发散问题，可以把网络平均路径长度定义为存在连通路径的节点对之间的距离的平均值。这种方法对于存在一个包含相当部分节点的连通巨片的网络较为适合。
另一种方法是把平均路径长度定义为网络中两点之间距离的简谐平均(Harmonic mean ) :

\[L = \frac{1}{GE} ,~~ GE= \frac{1}{\frac{1}{2}N(N-1) }\sum_{i\ge j}^{}d_{ij} \]

按照上式计算，两点之间距离为无穷大对应于距离的倒数为零，由此得到的平均路径长度总是有限值。
如果我们认为两个节点之间距离越短，在它们之间发送信息的效率越高，也就是假设两节点之间发送信息的效率与它们之间距离的倒数成正比，那么式中的GE就定量反映了网络中节点之间发送信息的平均效率，因此GE也称为全局效率( Global efficiency)。

网络直径(Diameter)

网络中任意两个节点之间的距离的最大值称为网络的直径( Diameter)，记为D，即

\[D= \max_{i,j} d_{ij} \]

考虑到实际网络往往并不是连通的，而是存在一个连通巨片，
因此，在实际应用中，网络直径通常是指任意两个存在有限距离的节点(也称连通的节点对)之间的距离的最大值。

进一步地，我们可能更为关心的是网络中绝大部分用户对之间的距离。
为此，可以统计网络中距离为 d 的连通的节点对的数量 占 整个网络中连通的节点对数量的比例，记为f(d);
并进而统计网络中距离不超过 d 的连通的节点对的数量 占 整个网络中连通的节点对数量的比例，记为g(d)。
例如，下图显示了在 5 个不同的时间采集得到的全球和美国的Facebook朋友关系网络中具有给定距离的用户对 所占的比例。

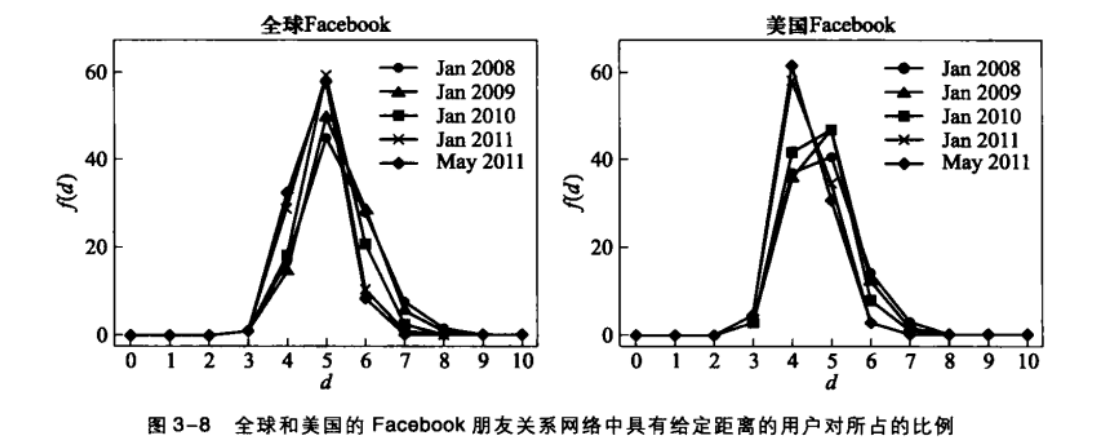
下图显示的则是2011年5月份的全球和美国的Facebook朋友关系网络中距离不超过给定值的用户对所占的比例。

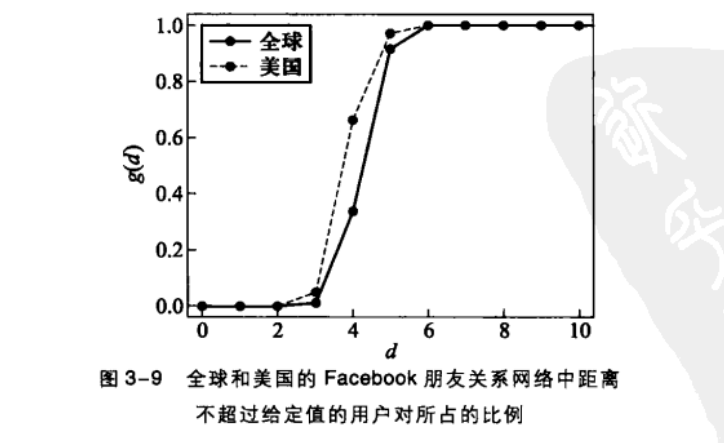
对于全球Facebook而言，任意两个用户之间距离不超过5的概率是92% ，不超过6的概率高达99.6% !
一般地，如果整数 D 满足：

\[g(D-1)<0.9, ~~ g(D) ≥ 0.9 \]

那么就称 D 为网络的有效直径(Effective diameter)。
换句话说，D 是使得至少90%的连通的节点对可以互相到达的最小的步数。
我们可以通过插值的方式把有效直径推广到非整数的情形。为此，对任一实数r ，假设 d ≤ r < d+1，通过线性插值的方式定义g(r)如下:

\[g(r) = g(d) +(g( d +1) - g( d) )(r - d) \]

如果实数D满足g(D) =0.9 ，那么就称 D 为网络的有效直径。
从实际计算的角度看，整数和非整数的有效直径定义之间的区别是可以忽略的。
有效直径通常是一个比直径更为鲁棒的量，
因为去除网络中少许几条边之后有可能会使原先距离较近的两个节点之间的距离变得很长，但对网络的有效直径并没有明显影响。

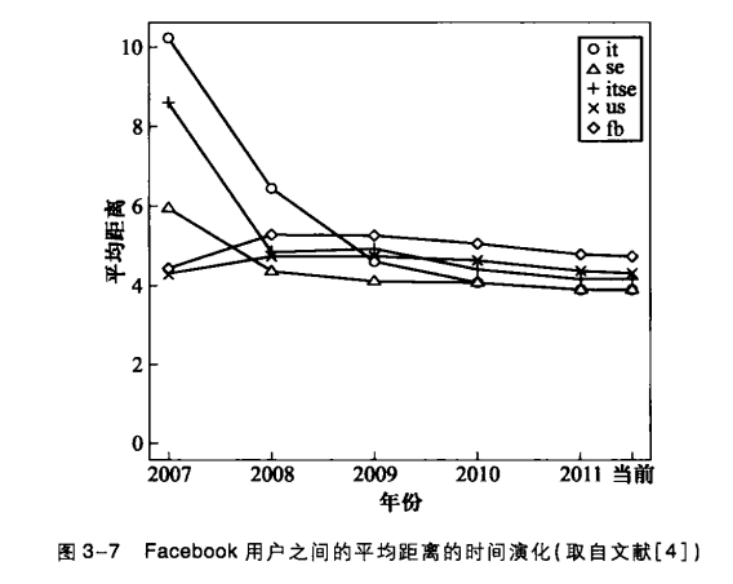
上图说明了Facebook 网络的平均距离随着时间的演化而呈现越来越小的趋势。
研究表明，许多实际网络的直径和有效直径都呈现越来越小的趋势，也称为直径收缩( Shrinking diameters)现象。

加权有向网络情形

上述关于无权无向网络的讨论都可以推广到加权和有向的情形，只是需要注意在加权情形需要考虑边的权值，在有向情形需要考虑边的方向。

对于加权无向网络，
两个节点之间的最短路径定义为连接这两个节点的边的权值之和最小的路径。
两个节点之间的距离即为最短路径上边的权值之和。

对于加权有向网络，
从节点A到节点B的最短路径是指从节点A到节点B的权值之和最小的有向路径。

在加权网络中，两个节点之间边数最少的路径并不一定是权值之和最小的路径。
在有向网络中，从节点A到节点B的距离可能并不等于从节点 B 到节点 A 的距离，甚至可能存在从节点A到节点B的有向路径但是不存在从节点B到节点A的有向路径。

求解加权有向网络上两点之间最短路径的经典算法是 Dijkstra算法。
该算法可以计算从一个源节点 s 到网络中所有其他节点的最短路径，其基本想法是为每个节点 v 保留到目前为止所找到的从节点 s 到节点 v 的最短路径。

参考：

[1] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012