节点的度与网络稀疏性

目录

• 节点的度
  • 度(Degree)
  • 平均度(Average degree)
  • 出度(Out-degree)与入度(In-degree)
  • 出强度(Out-strength)与入强度(In-strength)
• 网络稀疏性与稠密化

---

返回 我的研究方向(Research Interests)

---

节点的度

度(Degree)是刻画单个节点属性的最简单而又最重要的概念之一。

度(Degree)

无向网络中节点 i 的度 \(k_i\) 定义为与节点直接相连的边的数目。
对于没有自环和重边的简单图，节点 i 的度 \(k_i\) 也是与节点 i 直接有边连接的其他节点的数目。

对于加权网络而言，度的概念仍然可以用，但是这时还可以定义节点的强度(Strength)。给定一个包含N个节点的加权网络G及其权值矩阵W=$ ( w_{ij})$。如果 G 是无向加权网络，那么节点 i 的强度定义为:

\[s_i=\sum_{j=1}^{N}w_{ij} \]

平均度(Average degree)

网络中所有节点的度的平均值称为网络的平均度(Average degree)，记为(k〉。

给定网络G的邻接矩阵A = \((a_{ij})_{N*N}\) ，我们有

\[K_i = \sum_{j=1}^{N}a_{ij}=\sum_{j=1}^{N}a_{ji} \]

\[<K> = \frac{1}{N}\sum_{i=1}^{N}K_{i} = \frac{1}{N}\sum_{i,j=1}^{N}a_{ij} \]

网络节点的度与网络边数 M 之间有如下关系:

\[2M = N<K>=\sum_{i=1}^{N}K_i=\sum_{i,j=1}^{N}a_{ij} \]

即有

\[M = \frac{1}{2}N<K>=\frac{1}{2}\sum_{i=1}^{N}K_i= \frac{1}{2}\sum_{i,j=1}^{N}a_{ij} \]

\[<K> = \frac{2M}{N} \]

出度(Out-degree)与入度(In-degree)

有向网络中节点的度包括出度(Out-degree)和入度(In-degree)。

节点 i 的出度 \(k_{i}^{out}\) 是指从节点 i 指向其他节点的边的数目：

\[K_{i}^{out}=\sum_{j=1}^{N}a_{ij} \]

节点 i 的人度 \(k_{i}^{in}\) 是指从其他节点指向节点 i 的边的数目：

\[K_{i}^{in}=\sum_{j=1}^{N}a_{ji} \]

一个看似平凡实则寓意深刻的事实是：
在有向网络中，尽管单个节点的度和人度可能并不相同，网络的平均出度\(〈K_{i}^{out}〉和平均入度〈K_{i}^{in}〉\)却是相同的，
即有:

\[〈K_{i}^{out}〉=〈K_{i}^{in}〉=\frac{1}{N}\sum_{i,j=1}^{N}a_{ij}=\frac{M}{N} \]

从有向网络的定义看，上式是显然成立的。而且，它代表了一类复杂系统的一个重要特性:

对于系统中每个个体而言不一定成立的性质，却会在整个系统的层面上成立。

WWW、微博用户之间的关注网络、论文引用网络等都是具有这种特性的有向网络。
这里以打电话为例说明。每个人累计打出电话的次数和接听电话的次数一般而言不会恰好相等，但是全球打出电话的次数和接听电话的次数总是相等的。

出强度(Out-strength)与入强度(In-strength)

如果 G 是有向加权网络，那么节点i的出强度(Out-strength)和入强度(In-strength)分别定义为：

\[s_{i}^{out}=\sum_{j=1}^{N}w_{ij} \]

\[s_{i}^{in}=\sum_{i=1}^{N}w_{ij} \]

网络稀疏性与稠密化

一个包含 N 个节点的网络的密度(Density)ρ 定义为网络中实际存在的边数 M 与最大可能的边数之比。
因此，对于无向网络，网络的密度(Density)ρ 有：

\[ρ = \frac{M}{\frac{1}{2}N(N-1)} \]

对于有向网络，上式分母中的1/2去掉即可：

\[ρ = \frac{M}{N(N-1)} \]

实际的大规模网络的一个通有特征就是稀疏性：网络中实际存在的边数要远小于最大可能的边数。
例如，2011年5月的Facebook朋友关系网络包含7.21亿个活跃用户和687亿条边，网络平均度〈K〉≈ 190，密度\(ρ ≈0.3×10^{-7}\)，意味着这是一个很稀疏的网络。

实际网络的规模一般也都是随时间而演化的，而且许多实际网络中节点和连边的数量总体上在相当长的时间里都是呈现增加趋势的。
因此，一个自然的问题是：随着时间的演化，网络是变得越来越稀疏，还是越来越稠密？此时，平均度〈k〉是一个更为合理的刻画网络稀疏性(或稠密性)的指标。
因此，平均度和网络密度之间具有如下的简单关系:

\[<K> = \frac{2M}{N}=(N-1)ρ≈Nρ \]

将时刻t网络中的节点数和边数分别记为N(t)和M(t)。
如果两者呈线性比例关系，即M(t) ~ N(t)，那么上式可见，平均度〈k〉为―常数。
另一方面，如果两者呈平方关系，即M(t) ~ \(N^2(t)\)，那么就意味着，平均而言，每个节点都会与网络中一定比例的其他节点直接相连，整个网络会演化为一个非常稠密的网络。
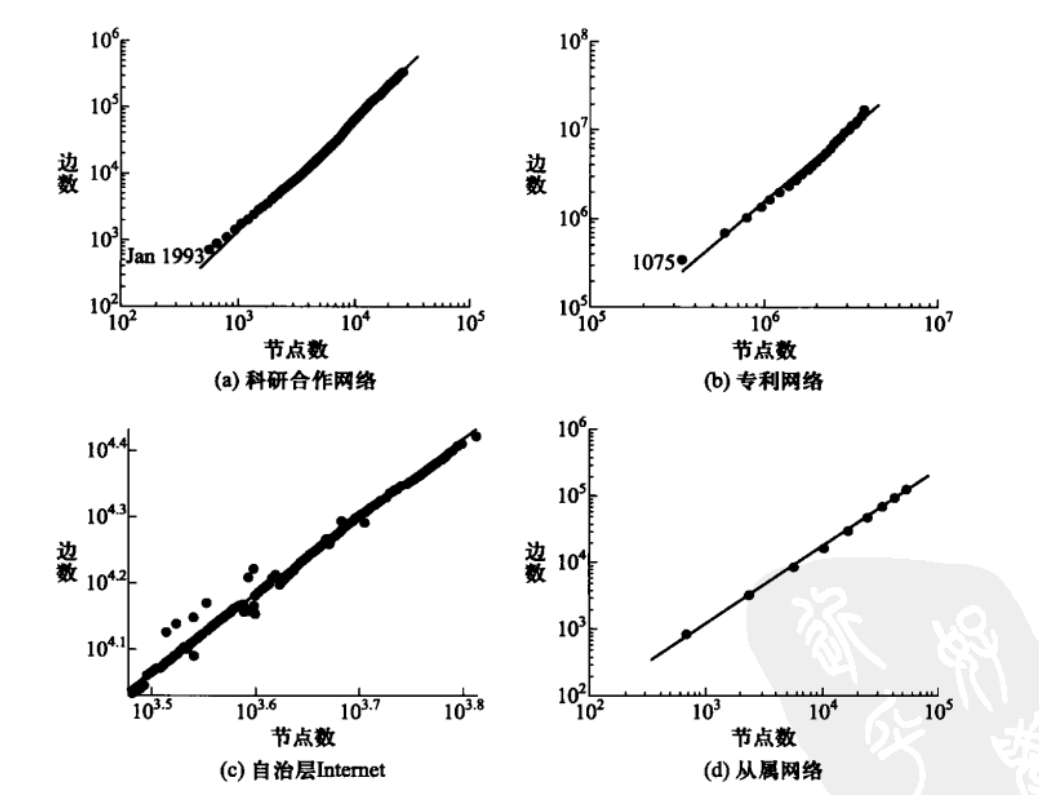
研究表明，许多实际网络的演化是介于上述两种情形之间的，即服从如下的超线性关系，也称为稠密化幂律( Densification power law )：

\[M(t) - N^a(t),~~ 1<a<2 \]

这意味着，
一方面，相对而言，实际网络会随着时间的演化而变得越来越稠密；
另一方面，与稠密的全耦合网络相比，实际网络仍然是稀疏的。

对上式两边取对数，可以得到:

\[ ln M(t) ≈ aln(N(t))+c,~~ 1<a<2 \]

其中C为一常数。
这说明\(ln M( t)\)是 \(In N( t)\)的线性函数，也就是说，如果以\(ln N(t)\)为横轴、 \(In M(t)\)为纵轴，我们应该会看到一条斜率为 α 的直线。
由于横轴和纵轴都采用了对数坐标，我们称对应的坐标系为双对数坐标系。
下图显示了双对数坐标系下的4种实际网络的节点数和边数之间的演化关系，可以看到它们都近似可以用斜率α∈ ( 1，2)的直线拟合。图(a)—(d)对应的 α 值分别为1.68，1.66，1.18和1.15。

参考：

[1] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012