无向网络中的巨片(Giant component)-有向网络中的蝴蝶结结构(Bow-tie structure)
尽管网络科学和传统的图论关于基本概念的定义是一致的,但两者在研究角度和研究方法上有着重要的区别。
传统的图论往往着眼于具有某种规则结构或者节点数较小的图,因而往往在理论分析时可以采用图示的方法直观地看出图的某些性质(如是否连通)。
然而,近年网络科学研究中涉及的实际网络往往包含数十万甚至数百万以上的节点,而且具有复杂的不规则拓扑结构。对于如此大规模的网络不可能通过图示的方法看出网络的拓扑性质,而必须借助于强大的计算能力和统计方法。
此外,网络科学不仅关注拓扑结构,而且更为关注拓扑结构的演化及其与网络上的动力学行为之间的关系等。
网络规模尺度上的巨大差异使得传统图论和网络科学对所研究的相关问题的表述都会不一样。
例如,在图论中,如果去除某个顶点就使得一个图从连通变为不连通,那么该顶点就称为割点(Cut-vertex) ;如果去除某条边就使得一个图从连通变为不连通,那么这条边就称为桥( Bridge)。
但是,在规模巨大的复杂网络中,去除单个节点或单条边往往并不能对网络的拓扑性质(如连通性)产生如此大的本质影响。
因此,网络科学更为关心的是:要去除网络中多少比例的节点或者边才能对网络的某个性质(如最大连通片的大小)产生本质影响?不同的去除策略是否会产生显著不同的后果?对网络的某种性质如何提高其对节点和边的去除鲁棒性?等等。
从更一般的科学范围看,研究个体数量较少的系统和研究个体数量极大的系统往往采用不同的方法:在物理学中,前者可以采用精确的方法,如经典力学;后者则往往需要采用统计的方法,如统计力学。对于这种差异,经典的陈述是诺贝尔奖得主、物理学家Anderson于1972年在《Science》上发表的一篇挑战还原论的经典文章“多则不同( More is different)”。文中立场鲜明地指出:
“由大量基本粒子构成的复杂系统的集体行为并不能依据少数粒子的性质做简单外推就能理解。正好相反,在复杂性的每一个层次都会呈现全新的性质,而要理解这一行为所需要做的研究,就其基础性而言,与其他研究相比毫不逊色。”
从哲学的观点看,这就是从量变到质变。例如,单个铜原子是不会导电的,因为电子被原子核拉住了。然而,由数量巨大的铜原子构成的一根铜丝却能导电。这种导电特性就是巨量的铜原子聚合之后所涌现出的一种新的与单个铜原子完全不同的特性。日常生活中有许多这样的由数量巨大的个体组成的系统会涌现出与单个个体不同的性质的例子。
近年来,人们在刻画复杂网络结构的统计特性上提出了许多概念和方法,并且利用了统计物理中的许多方法,包括相变和渗流理论、平均场理论、主方程方法等。2002年 Barabasi和 Albert发表的综述文章的标题就是“复杂网络的统计力学”。
复杂网络的连通性
无向网络中的巨片(Giant component)
网络平均距离和直径等概念严格说来只有对于连通图才是有限值。
经验和实证研究表明,许多实际的大规模复杂网络都是不连通的,但是往往会存在一个特别大的连通片,它包含了整个网络中相当比例的节点,这一连通片称为巨片( Giant component) 。
如下图所示,具有单个连通巨片的网络示意:

一些关于网络的拓扑性质的研究往往是针对巨片来进行的。实际网络中不仅往往存在巨片,而且巨片几乎总是唯一的。这一点仍然可以通过对社会网络的直觉来推断。假设社会网络中存在两个巨片,每个都包含数以千万计甚至数以亿计的人,只要某一天分别属于两个片的两个人偶然相识,也就在这两个片之间对应地有一条边相连,那么这两个巨片就合并成为了一个更大的巨片。
再有一个实例是全球最大的社交网站Facebook上的活跃用户之间的朋友关系网络。
2011年5月, Facebook 上大约有7.21亿个活跃用户以及687亿条朋友关系链,节点数超过当时全球人口的10%。
这里,如果一个Facebook注册用户在2011年5月测量数据之前的最近28天时间里至少登录过一次并且至少有一个Facebook朋友,那么就称该用户为活跃用户,这里把那些只是注册过但几乎从不使用或者没有朋友的孤立用户剔除掉。
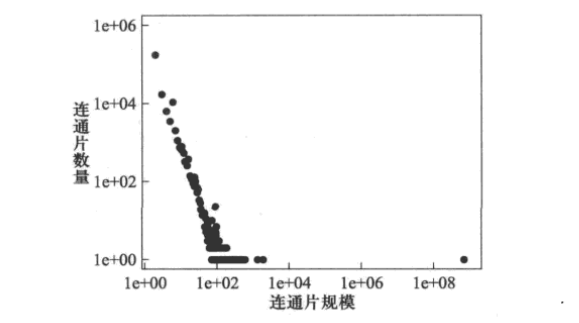
对于一个包含多个连通片的网络,可以绘制该网络的连通片规模的分布。
下图给出了双对数坐标下Facebook 网络中不同规模的连通片的数量。图中最右端的一个黑点对应于最大的连通片(即巨片),它包含了网络中99.91%的节点。其余的连通片数量很多但规模都很小,第二大连通片仅包含不到3 000个节点。
有向网络中的蝴蝶结结构(Bow-tie structure)
实际的大规模有向网络往往既不是强连通也不是弱连通的,但是许多有向网络往往有一个包含了网络中相当部分节点的很大的弱连通片,称为弱连通巨片( Giant weakly connected component,GWCC)。这一弱连通巨片又往往具有一种包含4个部分的蝴蝶结结构(Bow-tie structure) :
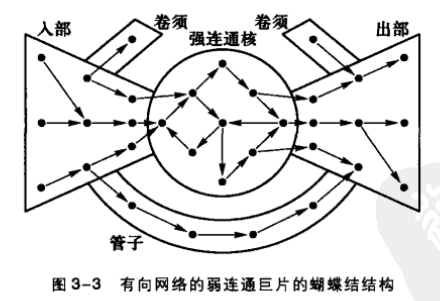
强连通核( Strongly connected core , SCC)
也称为强连通巨片(Giantstrongly connected component),它位于网络的中心。SCC中任意两个节点之间都是强连通的,即存在从任一节点到另一节点的有向路径。
入部(IN)
包含那些可以通过有向路径到达SCC但不能从SCC到达的节点。
也就是说,一定存在从IN中任一节点到SCC中任一节点的有向路径;反之,从SCC中任一节点出发沿着有向边都无法到达IN中的一个节点。
出部(OUT)
包含那些可以从SCC通过有向路径到达但不能到达SCC的节点。
也就是说,一定存在从SCC中任一节点到OUT中任一节点的有向路径;反之,从OUT中任一节点出发沿着有向边都无法到达SCC中的一个节点。
从IN中任一节点到OUT中任一节点必然存在有向路径,而且该路径必经过SCC中的某些节点。
卷须(Tendrils )
包含那些既无法到达SCC也无法从SCC到达的节点。
对于挂在IN上的任一卷须节点,必至少存在一条从IN中某一节点到该节点的不需经过SCC的有向路径;
对于挂在OUT上的任一卷须节点,必至少存在一条从该节点到OUT中某一节点的不需经过SCC的有向路径。
此外,还有可能存在从挂在IN上的卷须节点到挂在OUT上的卷须节点的不经过SCC的有向路径,这些串在一起的卷须节点称为管子(Tube)。
下表和下图说明的是超过2亿个页面和15亿个链接的WWW样本的蝴蝶结结构。

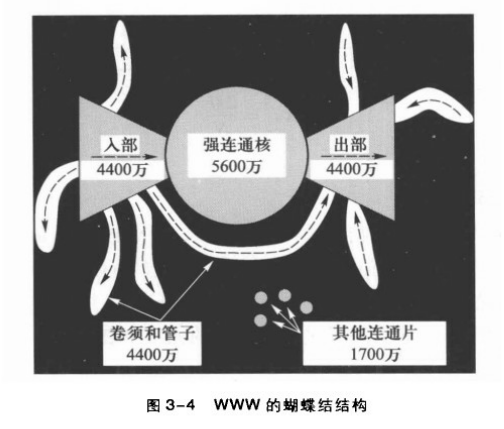
在 WWW 样本上:
- 包含30%左右网页的强连通核,对应于可以通过鼠标点击超链接在有限步内互相到达的“核心网页”。
- 包含24%左右网页的入部,对应于可以通过超链接在有限步内到达“核心网页”但是无法返回的“源网页”。
例如,你设计的一个网页上有超链接指向某个“核心网页”,但通常并不存在从“核心网页”指向你的网页的超链接。 - 包含24%左右网页的出部对应于从“核心网页”的链接中指出来却无法回到“核心网页”的“目标网页”。
例如,你在搜索文章时,从Google 主页开始,找到某位教授的主页,然后找到该教授的文章列表,然后点击相应的文章。但是你从该文章对应的页面通常无法通过超链接再返回到Google主页。
当然,强连通核未必一定就是蝴蝶结结构中节点数最多的部分。
例如,Vitali等人研究了由全球43060家跨国公司基于股权所有关系构建的有向的经济网络,在该网络的蝴蝶结结构中,出部是最大的部分,而强连通片只占很小部分。蝴蝶结也是生物网络中常见的一种结构”。从更一般的意义看,蝴蝶结作为复杂的技术和生物网络中常见的一种系统结构可能有助于在效率、鲁棒性和进化能力等方面保持一种平衡。
参考:
[1] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012


 浙公网安备 33010602011771号
浙公网安备 33010602011771号