二分网络-匹配问题-G-S算法
二分图( Bipartite graph)
给定图G = (V,E)。如果顶点集V可分为两个互不相交的非空子集 X 和 Y ,并且图中的每条边(i,j)的两个端点i和j分别属于这两个不同的顶点子集,那么就称图 G 为一个二分图( Bipartite graph),记为G= (X,E,Y)。
如果在子集X中的任一顶点i和子集Y中的任一顶点j之间都存在一条边,那么就称 图G 为一个完全二分图( Complete bipartite graph)。
在网络科学研究中,二分图也称为二分网络(Bipartite network )、从属网络( Affiliation network)或二模网络( Two-mode network )。
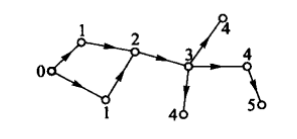
判断任意一个连通的网络是否为二分网络的一般方法如下:在网络中任意选取一点,把该节点以及与该节点距离为偶数的所有其他节点的集合记为X,把与该节点的距离为奇数的节点的集合记为Y。如果在集合X和Y的内部都不存在边,即所有的边都只存在于集合X和Y之间,那么该网络就是二分网络。
下图中的初始节点为0,箭头表示寻找集合X 和 Y中的节点时的次序。
在通俗的理解下:
二分网络(或二分图)是这样一种网络:其节点可以分成两个不相交的节点集合U和V,使得每个链接都连接着一个U中的节点和一个V中的节点。换句话说,如果我们把集合U中的节点涂成绿色,把集合V中的节点涂成紫色,则每个链接连接着颜色不同的两个节点。
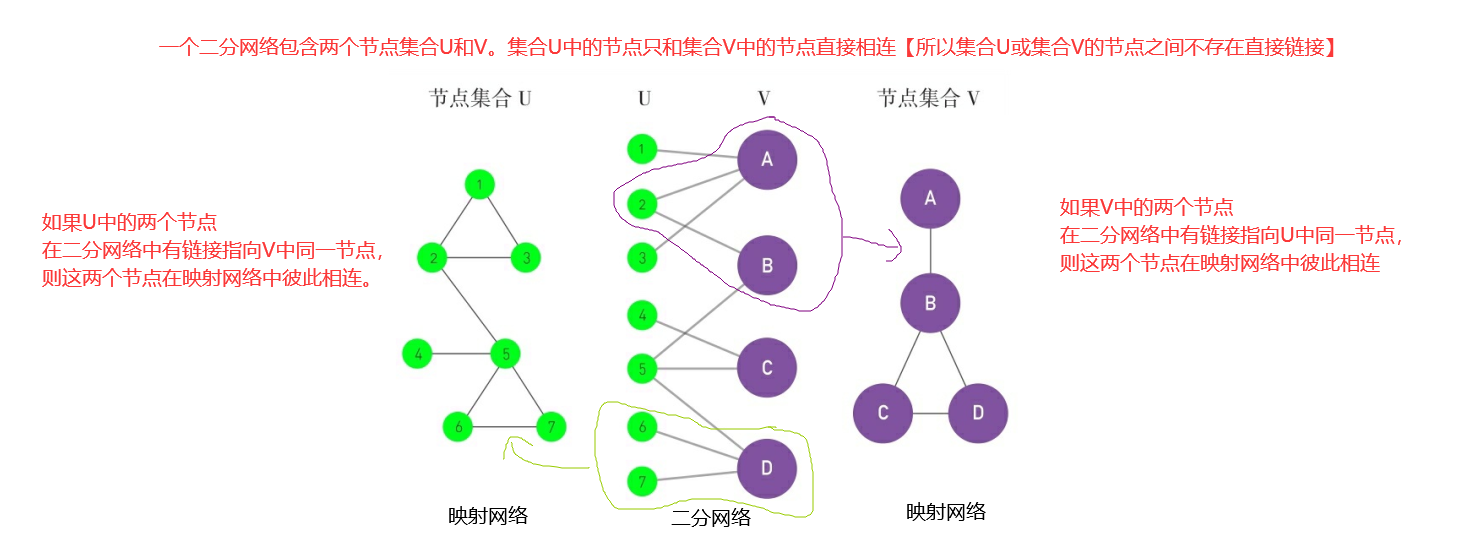
网络科学研究中,我们会碰到很多二分网络。一个著名的例子是好莱坞电影演员网络,其中一个节点集合对应着电影(记为U),另一个节点集合对应着演员(记为V)。如果某个演员出演了某部电影,则二者之间有一个链接。该二分网络的一个映射网络是演员网络——出演过同一部电影的两个演员之间彼此相连。另一个映射网络是电影网络——至少有一个演员相同的两部电影彼此相连。
二分图的匹配
二分图是一种十分有用的网络模型,许多涉及资源和人员分配的实际问题都可以归结为二分图的匹配问题(Matching problem) ,具体定义如下:
(1)匹配(Matching):设G=(X,E,Y)为二分图,F为边集 E 的一个子集,即F 包含于 E。如果F中任意两条边都没有公共端点,那么就称F为图 G 的一个匹配。
(2)最大匹配(Maximal matching):图 G 的所有匹配中边数最多的匹配。
(3) X-完全匹配( X-Perfect matching):集合X中任一顶点均为匹配F中 边的端点。
(4)Y-完全匹配( Y-Perfect matching):集合Y中任一顶点均为匹配F中 边的端点。
(5)完全匹配( Perfect matching):F既是X-完全匹配又是Y-完全匹配,此时,集合X和集合Y中的顶点恰好 一 一 对应。
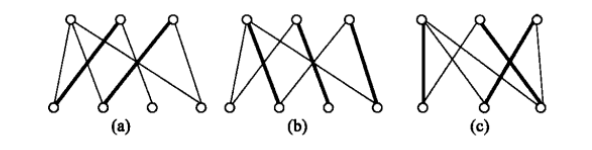
例如,在下图中,粗线表示匹配中的边(简称匹配边)。
图( a)中的匹配不是最大的;图(b)中的匹配是最大的,X-完全匹配;图(c)中的匹配是完全的(从而也是最大的)。
稳定匹配
稳定匹配的定义
寻找二分图的一种特定的完全匹配
稳定的完全匹配的算法是由两个数理经济学家Gale和Shapley于20世纪60年代提出的,因此称为Gale-Shapley 算法(简称G-S算法)。
这里以硕士研究生与导师之间的双向选择为例来说明稳定匹配问题及其求解算法。
师生分配问题
假设硕士研究生人学后的前两周是师生双向选择的时间,通常学生人数要比教师人数多,系里会对每位老师当年能够招收的研究生设定一个上限,例如至多招3名学生。
师生分配方案的基本要求是:每位学生必须有且只能有一名导师,每位导师至多只能带3名学生。
系里每年会把所有研究生指导教师的信息提供给所有学生,然后每位学生根据对这些教师的了解及其个人兴趣挑选一些老师,并前去与这些老师面谈。面谈期间往往会发生类似如下的情形:
学生S1、先是去找教师P1,教师P1觉得该学生不错就考虑接受该学生;
后来学生S1、又去找了教师P2并觉得更愿意跟随教师P2,而教师P2也觉得该学生不错,于是学生S1就选了教师P2,
这时教师P1会从他面试过的学生中再挑选一名学生S2,而本来教师P3已经答应接受学生S2的,现在学生S2觉得教师P1,更适合他,于是学生S2可能就选择教师P1而离开教师P3,如此下去有可能引发一系列的连锁反应。问题是最终能否得到一个稳定的分配方案?
我们首先对问题做进一步的简化而又保持其本质特征。这里的核心问题是要在许多种可能的分配方案中找到一种稳定的分配方案,学生数比教师数多多少并不是本质问题。
因此,我们不妨假设学生数和教师数一样多且每位教师恰好带一名学生。
现在可以给出该问题的完全二分图表示 G = (X,E,Y),其中X是所有学生的集合,Y是所有教师的集合,两个集合的人数都为 N 且任一学生和任一教师之间都有一条边相连。
例如,下图是一个包含3个学生和3个教师的完全二分图。
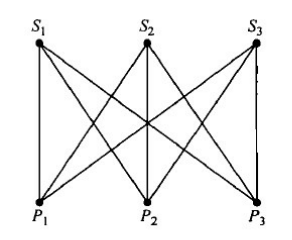
一种师生分配方案就对应于完全二分图G的一个完全匹配(即一一对应)。图G共有N!种完全分配,对应于N!种可能的师生分配方案。
用蛮力方法比较每一种分配方案显然是不切实际的。在介绍G-S算法之前,我们先给出稳定的分配方案的如下定义。
一种师生分配方案称为是稳定的( Stable) ,如果该方案能够保证:
1、如果有学生想要换导师,那么没有其他教师愿意接受这位学生;
2、如果有教师想要换学生,那么没有其他学生愿意跟随这位教师。
我们可以对稳定分配方案的定义做进一步的形式化处理。为此,假设:
每个学生都有一个优先表用于对所有教师进行排名:在这个学生的优先表中排名越靠前的教师就是这个学生越想跟随的教师。
每个教师也有一个优先表用于对所有学生排名:在这个教师的优先表中排名越靠前的学生就是这个教师越想招的学生。
假设所有优先表都不允许出现并列排名。
一种师生分配方案是稳定的,如果对每一个教师Р和每一个没有跟随教师P的学生S,至少出现下列两种情形之一:
1、教师Р对他已经接受的每位学生都比对学生S更满意;
2、学生S对他目前的导师比对教师Р更满意。
由这一形式化的定义,我们可以立即知道什么是不稳定的分配方案:
一种师生分配方案是不稳定的(Unstable) ,如果至少存在一个教师Р和一个没有跟随教师P的学生S,使得以下两点均满足:
1、教师Р对学生S至少比他所接受的学生中的一位更满意;
2、学生S对教师P比对他目前的导师更满意。
我们称教师Р和学生S是这种分配方案的一对不稳定的因素。
稳定匹配的求解
对每组给定的优先表,是否一定存在稳定的分配方案?如果存在,是否能够有效地求出来?
为了进一步获得感性认识,我们先看一下最简单的例子:
假设只有两个学生{S1,S2}和两个教师{Pl,P2}。
此时只有两种可能的分配方案:
方案一:(S1,P1),(S2,P2);
方案二:(S1,P2),(S2,P1)。
假设学生和教师的优先表如下:
- 学生S1,更想跟随教师P1而不是P2;学生S2更想跟随教师P1而不是P2。
两个学生对教师的排序完全一致:都更想跟随教师P1。 - 教师P1,更想招收学生S1而不是S2;教师P2更想招收学生S1而不是S2。
两个教师对学生的排序也完全一致:都更想招收学生S1。
此时,
方案一是唯一的稳定分配方案:学生S1和教师P1都很满意,他们不会想分开,而学生S2和教师P2想分开也办不到;
方案二则是不稳定的:学生S1想离开教师P2而跟随教师P1,而教师P1也想放弃学生S2而接收学生S1。
现在假设学生和教师的优先表如下:
- 学生S1更想跟随教师P1而不是P2;学生S2更想跟随教师P2而不是P1
各自更想跟随不同的教师。 - 教师P1更想招收学生S2而不是S1;教师Р2更想招收学生S1而不是S2
各自更想招收不同的学生。
此时,
方案一是稳定的分配方案:两个学生已经得到最满意的结果;
方案二也是稳定的分配方案:两个教师已经得到最满意的结果。
这个简单的例子说明有可能存在不止一种稳定的分配方案。
在目前实际采用的师生面谈过程中,一批学生可能会同时与一批教师面谈。
为进一步简化,我们假设每次只有一位学生与教师面谈。在前述简化假设条件下,求解稳定的师生分配方案的G-S算法叙述如下:
每次只选择一位学生S,让他(她)按照自己的优先表从高到低依次找还没有面谈过的教师面谈。
为公平起见,我们假设这位学生是通过完全随机的方式选出来的。如果与他(她)面谈的教师目前没有候选的学生,那么这位教师最安全的做法就是把这位学生列为候选学生,即使这个学生未必是这位老师的优先表中靠前的学生,因为每位教师必须要带一名学生。如果这名教师已经有了候选学生S',那么他将应该比较学生S和学生S',并从中挑选一个作为他的候选学生。按照这一程序,学生S必然在这一轮面谈后被某个教师考虑为候选学生。
然后,再随机选择一位自由的(即还没有成为候选对象的)学生,让他(她)按照自己的优先表从高到低依次找自己还没有面谈过的教师面谈,直到成为候选学生。这一迭代过程一直进行下去,直到所有学生都成为候选学生或每一个自由的学生都与所有教师面谈过为止。
在研究上述算法性质时,首先要注意到,尽管只有N个学生,该算法一般说来未必在N步之后就终止。这是因为,已经成为候选学生的人有可能在后面的某次迭代中被另一位同学顶替掉而再次成为完全自由的学生。因此,针对该算法我们依次需要考察如下问题:该算法是否会终止?如果会,迭代多少步之后终止?该算法是否能够得到一个完全匹配?如果能,这个完全匹配是否一定为稳定匹配?
在回答这些问题之前,首先注意到算法的几个似乎是让学生越来越沮丧,教师越来越高兴的基本事实:
- 事实一:教师Р从第一次有学生去和他面谈开始,就一直会有候选学生,而且他的候选学生只会越变越好(按照教师Р的优先表);
- 事实二:学生S可能会在候选学生和自由学生状态之间交替,而且他(她)去面谈的教师只会越变越差(按照学生S的优先表)。
- 事实三:如果学生S在算法的某一步是自由的,那么此时,必至少存在一位该学生没有面谈过的教师。
事实三意味着算法终止的唯一条件为所有的学生都是候选学生,即找不到自由的学生。
现在我们有如下结论:
G-S算法在至多\(N^2\)次迭代之后终止,且算法终止时所得到的集合是一个完全匹配。
G-S算法终止时所得到的集合一定是一个稳定匹配。
参考:
[1] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012


 浙公网安备 33010602011771号
浙公网安备 33010602011771号