树-生成树-最小生成树-Kruskal 算法-Prim算法
树（Tree）
一个包含 N 个顶点的连通图 G 至少含有 N-1 条边。
如果这个连通图 恰好 只有 N-1 条边，那么这个图就可以看做是最简单的连通图，我们称之为树(Tree)。
一般地，一个包含 N 个顶点的无向图 G 称为一棵树，如果它满足如下任意一个条件:
- 图 G 是连通的并且有 N-1 条边
- 图 G 是连通的并且不包含圈
- 图 G 不包含圈并且有 N-1 条边
- 图 G 中任意两个顶点之间有且只有一条路径
- 图 G 中任意一条边都是桥，即去掉图 G 中任意一条边都会使图变得不连通
例如：图(a)给出的就是一棵包含9个顶点的树。这棵树也称为自由树，因为用肉眼一下子很难看出来树根、树枝和树叶等人们日常生活中形成的关于树的基本特征。
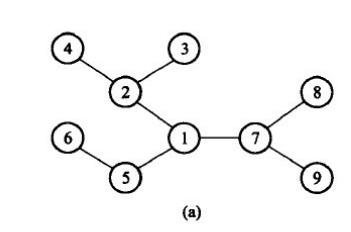
然而，通过把某个顶点设定为根(Root) ，就可以得到树的层次表示，称为根树(Rooted tree)。
例如，对于图(a)的树，我们取顶点1为根，就可以得到如图(b)所示的根树。对于大型复杂网络而言，层次性的描述和分析方法是非常重要的。
最小生成树(Minimum spanning tree,MST)
如果一个连通图本身不是树，那么该图也可以看做是在一个树的基础上添加一些边而形成的，这就是生成树的概念。连通的无向图G的一个生成树( Spanning tree)是图G的一个子图，该子图是包含图G所有顶点的一个树。
一个包含 N 个顶点的连通图可能包含多个生成树，但每个生成树的边数一定都是 N-1 。
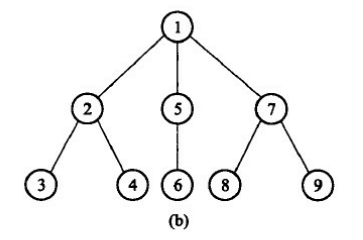
例如，下图给出的是一个包含5个顶点的连通图及其4个生成树。
一个顶点数目很大的图，其生成树的数目一般而言可能大得惊人。
例如，一个顶点标志了标号的完全图\(K_N\)的生成树个数\(τ(K_N)\)，有如下的Caylay 公式:
生成树的概念可以直接推广到加权无向图。此时，尽管每个生成树的边数仍然相同，然而每个生成树的边的权值之和却未必相同，其中权值之和最小的生成树就称为最小生成树( Minimum spanning tree,MST)。
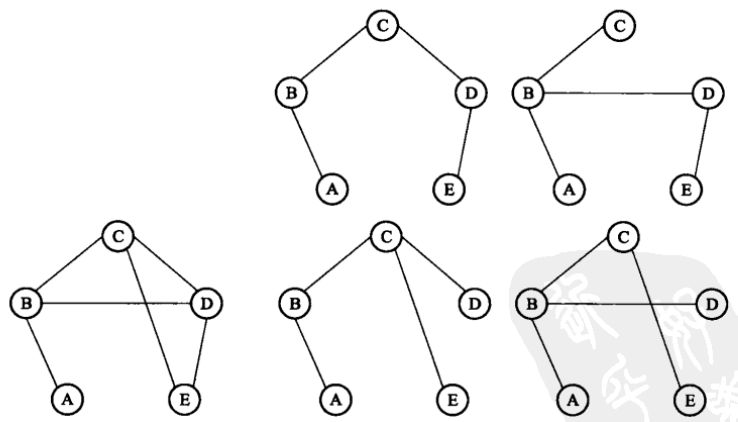
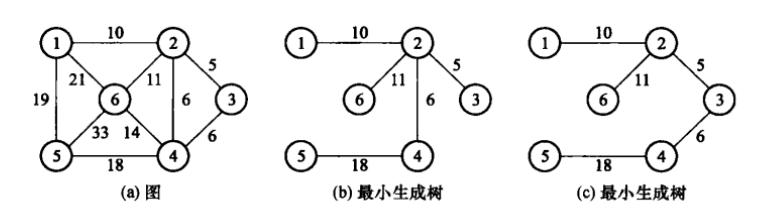
最小生成树不一定是唯一的。例如，下图给出了一个加权无向图的两个最小生成树。如果一个连通图中所有边的权值都互不相同，那么该图必然具有唯一的最小生成树。
最小生成树的概念在实际网络分析与设计中是很有用的。
一个典型的问题表述如下：
假设要在若干个地点之间建设一个连通的网络,这里的地点可以是国家、城市﹑建筑物等,网络可以是通信网络、交通网络、电力网络、供水网络等。假设我们可以计算出在任意两点之间建一条可行边所需的代价(如果两点之间完全不可能建边，可以定义代价为无穷大)。要使整个网络保持连通且建设代价最低，应该如何选择需要建设的边?
最小生成树构造算法往往是基于最小生成树的割性质(Cut property)和圈性质(Circle property)，这两个性质分别给出了一条边是否在最小生成树中的判别准则。
割性质(Cut property)
给定连通图 G=( V,E,W) 并假设所有边的权值(W)互不相同，则有：
令 S 是图 G 的任意顶点子集，S≠∅(空集) ，S≠V。令边 e 是一个端点在 S 中，另一端点在 V - S 中的最小权值边。那么图 G 的最小生成树必然包含边e。
圈性质(Circle property)
给定连通图 G=( V,E,W) 并假设所有边的权值(W)互不相同，则有：
令C是图G中的一个圈，并假设边e是圈C中权值最大的一条边，那么图G的最小生成树必然不包含边e。
正是由于最小生成树的上述两个性质，才使得人们可以很自然地设计出构造最小生成树的多种贪心算法：任何通过包含满足割性质的边 并 删除满足圈性质的边以得到一棵生成树的算法，最终得到的一定是最小生成树。
Prim算法和Kruskal算法是两个构造最小生成树的经典的有效贪心算法。
Prim算法的时间复杂度为O(M + Nlog N)，因此适合于计算边稠密的网络的最小生成树。
Kruskal算法的时间复杂度为O(Mlog M)(M为网络中边的数目)，因此适合于计算边稀疏的网络的最小生成树。
Kruskal 算法
假设G=(V,E,W)是一个具有N个顶点的连通图，T= (U,TE)为欲构造的最小生成树。
初始时，U =V，TE = ∅。将图 G 中的边按权值从小到大的顺序依次选取，若选取的边使生成树不形成圈，则把它加入TE中；若选取的边使生成树形成圈，则将其舍弃，如此进行下去，直到TE中包含 N–1 条边为止。
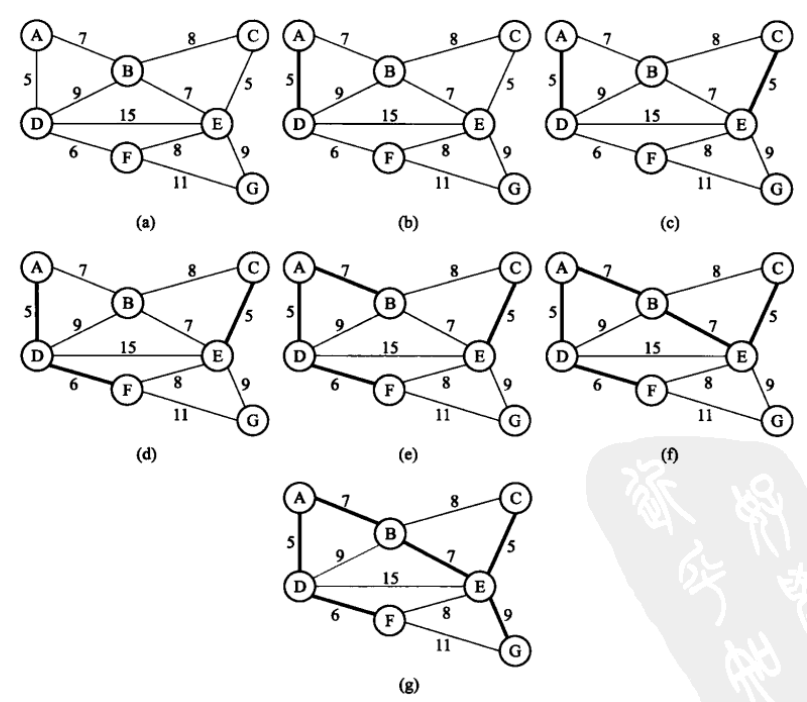
下面是一个利用Kruskal 算法求最小生成树的例子：
1、原始图是一个包含7个顶点的连通的加权图 (图(a));
2、添加边(A,D): (A,D)和(C,E)均为最短边，随机选择一条，这里选(A，D) (图(b));
3、添加边(C,E)：因为它是最短边，并且添加该边后不会形成圈 (图(c));
4、添加边(D,F)：因为它是最短边，并且添加该边后不会形成圈 (图(d));
5、添加边(A,B): (A,B)和(B,E)为最短边，随机选择一条 (图(e)) ;
舍弃边(B,D)：如果添加边(B,D)就会形成圈(A,B,D,A);
6、添加边(B,E)：因为它是最短边且添加后不会形成圈 (图(f));
舍弃边(B,C)：添加该边会形成圈(B,C,E,B);
舍弃边(D,E)：添加该边会形成圈(D,E,B,A,D);
舍弃边(F,E)：添加该边会形成圈(F,E,B,A,D,F);
7、添加边(E,G) ,得到一个最小生成树(图(g))。
参考：
[1] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012
