路径与连通性
路径相关定义
路径( Path)
无向图 G = ( V , E ) 中的一条路径是指一个顶点序列 P = \(v_1 v_2…v_k\) ，其中每一对相邻的顶点\(v_i\)和\(v_{i+1}\)之间都有一条边。Р也称为从\(v_1\)到\(v_k\)的一条路径，或简称为一条\(v_1\)-\(v_k\)路径。
一条路径的长度(Length)定义为这条路径所包含的边的数目。
回路(Circuit)
起点与终点重合的路径称为回路。
简单路径( Simple path)
各个顶点都互不相同的路径称为是简单的。
圈(Circle)
一条路径 P = \(v_1 v_2…v_k\) 称为是一个圈，如果它满足:
- k>2
- 前k-1个顶点互不相同
- \(v_1\) = \(v_k\)
也就是说，一个圈是从一个起点出发，经过互不相同的一些顶点，然后再回到起点的一条路径。因此，一个圈一定是一条回路，但一条回路可能包含多个圈。
在技术网络(如通信网络和运输网络)中有时会有意设计一些圈,以期通过边的冗余而实现网络鲁棒性。
下图显示的是Internet前身-----1970年的ARPANET的网络示意图,其中共有13个节点。该网络中的每条边都属于某个圈，其中长度最短的一个圈是SRI--STAN--UCLA--SRI，它只有三条边。
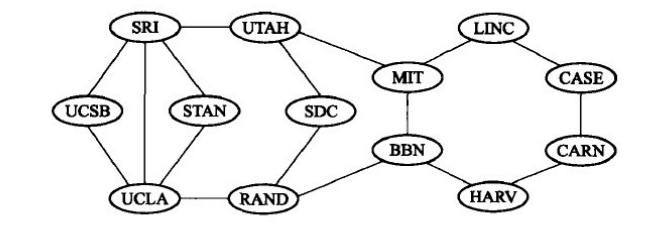
这种设计的好处是：网络中任意一条边失效，仍然可以从一个节点到达任一其他节点。
无向图连通性相关定义
连通的(Connected)与不连通的(Disconnected)
一个无向图称为是连通的(Connected) ，如果每一对顶点之间都至少存在一条路径；否则就称该图是不连通的(Disconnected)。
连通片(Connected component)
一个不连通图是由多个连通片(Connected component)组成的。
一个连通片是网络的一个满足如下两个条件的子图(Subgraph):
- 连通性：该子图中的任意两个顶点之间都存在路径
- 孤立性：网络中不属于该子图的任一顶点与该子图中的任一顶点之间不存在路径。
上述定义意味着，每一个不连通图都是由若干个不相交(即没有公共顶点)的连通片组成的。
最大连通片(Maximal connected component )
其中包含顶点数最多的连通片就称为最大连通片(Maximal connected component )。
例如，下图中的不连通图包含两个连通片，其中左边的包含8个顶点的连通片是最大连通片。
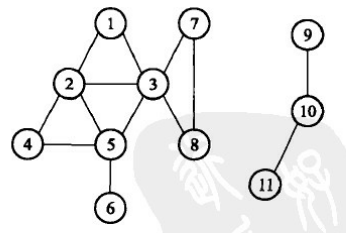
有向图连通性相关定义
强连通的( Strongly connected)
如果对于图中任意一对顶点 u 和 v ，都既存在一条从顶点 u 到顶点 v 的路径也存在一条从顶点 v 到顶点 u 的路径。则该有向图称为是强连通的( Strongly connected)
弱连通的(Weakly connected )
如果把图中所有的 有向边 都看做是无向边后所得到的无向图是连通的。则该有向图称为是弱连通的(Weakly connected)
通过另外一个等价定义可能更能明白为什么弱连通是弱的。在一个有向图中采取如下操作：如果两个顶点之间只有一条单向边，那么就添加一条反方向的边。如果经过这样添加边的操作之后所得到的新的有向图是强连通的，那么就称原来的有向图是弱连通的。
对于有向图的强连通性则需要考虑边的方向。
例如，下图所示的有向图是弱连通的但不是强连通的，该图包含分别位于3个虚框内的3个强连通片( Strongly connected component, SCC)。
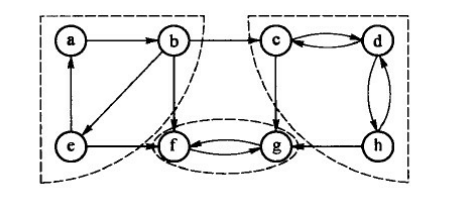
参考：
[1] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012
