邻接矩阵-邻接表-三元组
用计算机分析实际网络的性质面临的第一个问题就是如何在计算机中表示一个网络。
在传统的图算法中，两种最常见的表示图的基本结构是邻接矩阵( Adjacency matrix)和邻接表( Adjacency list)。
邻接矩阵( Adjacency matrix)
图G的邻接矩阵 A =\(( a_{ij})_{N*N}\)是一个N阶方阵，第 i 行第 j 列上的元素\(a_{ij}\)定义如下:
加权有向图
图中的边是有向的( Directed)和有权的(Weighted)。边是有向的是指存在一条从顶点i指向顶点j的边(i,j)并不一定意味着存在一条从顶点j指向顶点i的边(j,i)。对于有向边(i,j),顶点i称为始点，顶点j称为终点。边是有权的是指网络中的每条边都赋有相应的权值,以表示相应的两个节点之间的联系的强度。
我们以一个包含5个人的朋友关系网络为例来做说明。假设朋友关系可分为三类：一般、较好和很好，这三类关系分别用权值1、2和3表示。
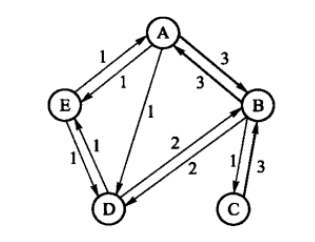
其邻接矩阵表示：
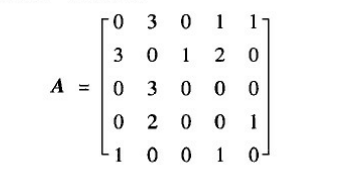
例如，上图对应的领接矩阵可以表示为：
加权无向图
图中的边是无向的( Undirected)和有权的。所谓无向的是指任意点对(i,j)与(j,i)对应同一条边。顶点i和j也称为无向边(i,j)的两个端点(End-points)。
例如，在5个人之间的加权有向的朋友关系网络中，如果把朋友关系定义为双方都认为对方是朋友，把两人之间的亲密程度定义为两人观点中的较低值，那么就得到下图所示的一个加权无向网络。
另一方面，也有一些实际网络本身确实就是加权无向图。一个典型的例子就是科研人员之间的合作网络，其中，每个科研人员为一个节点，两个科研人员如果合作发表过文章，那么就在相应的两个节点之间有一条边，边的权值对应于两个人合作发表论文的数量。
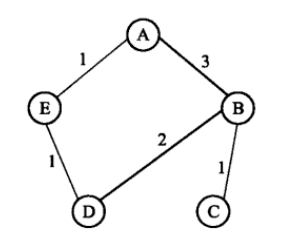
其邻接矩阵表示：
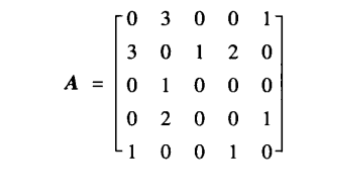
例如，上图对应的领接矩阵可以表示为：
无权有向图
图中的边是有向的和无权的( Unweighted)。所谓无权图实际上也可意味着图中边的权值都相等(通常可假设每条边的权值均为1)。
如果我们不需要考虑朋友关系的亲密程度(相当于把阈值取为О)，就得到下图所示的无权有向网络。
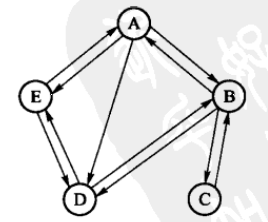
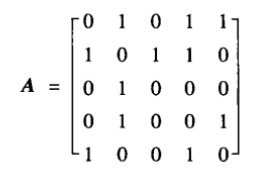
其邻接矩阵表示：
例如，上图对应的领接矩阵可以表示为：
无权无向图
图中的边是无权的和无向的。无权无向图可以通过对有向图的无向化处理和加权图的阈值化处理而得到。
如果把朋友关系定义为双方都认为对方是朋友并且不考虑关系的亲密程度的差异，那么朋友关系网络就是一个无权无向网络。
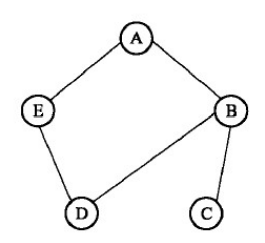
其邻接矩阵表示：
例如，上图对应的领接矩阵可以表示为：
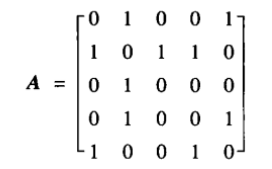
邻接表( Adjacency list)与三元组
实际的大规模复杂网络往往是很稀疏的，这意味着其对应的邻接矩阵中大部分的元素均为零，这样的矩阵称为稀疏矩阵。在计算方法中，针对稀疏矩阵有专门的节省空间的存储技术，邻接表和三元组表示就是找到这些边的有效的存储图的方法。
邻接表
在图算法中，表示稀疏的无权图的最常用方法是邻接表。它对每个顶点i建立一个单链表(即邻接表)，这个单链表由邻接于顶点i的所有顶点构成。
例如，无权有向图邻接表表示如下(图中的节点标号A ~ E分别替换为数字1 ~ 5 ):
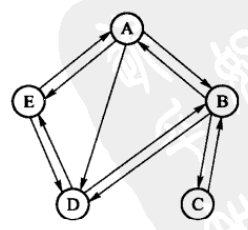
以第一行的1245为例，它表示有从顶点1分别指向顶点2、顶点4和顶点5的三条边。在无向图的邻接表中，每条边会出现两次。
三元组
www上有许多公开的实际网络数据，这些数据常见的一种表示方式是三元组形式。
三元组可以很容易地表示一般的加权有向图。
以下图中的含5个顶点的加权有向网络为例(图中的节点标号A ~ E分别替换为1 ~ 5)，其三元组表示形式如下:
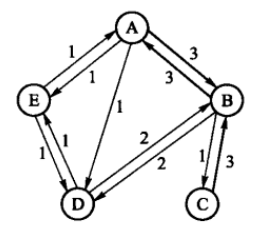
以第一行的三元组1 23为例，它表示有一条从顶点1指向顶点2的边，且该边的权值为3。在无向图的三元组表示中，每条边也会出现两次。
参考：
[1] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012
