数据降维-主成分分析(PCA)
目录
什么数据降维
数据降维可以理解为,从大量的特征中,选择比较有代表性的特征,从而在保证不丢失整体数据的特征的情况下,减少计算量。即数据的特征数量减少。多少个特征值【多少列】称为多少个维度
数据类型
-
离散型数据:
由记录不同类别个体的数目所得到的数据,又称计数数据,所有这些数据全部都是整数,而且不能再细分,也不能进一步提高他们的精确度。 -
连续型数据:
变量可以在某个范围内取任一数,即变量的取值可以是连续的,如,长度、时间、质量值等,这类整数通常是非整数,含有小数部分。
注:只要记住一点,离散型是区间内不可分,连续型是区间内可分
特征选择
就是单纯地从提取到的所有特征中选择部分特征作为训练集特征,特征在选择前和选择后可以改变值、也不改变值,但是选择后的特征维数肯定比选择前小,毕竟我们只选择了其中的一部分特征。
特征选择原因
- 冗余:部分特征的相关度高,容易消耗计算性能
- 噪声:部分特征对预测结果有负影响
主要方法
- Filter(过滤式) : VarianceThreshold
- 通过方差过滤,方差大小衡量数据里面,数据和平均值的偏差程度,
- 如果方差为0,name该特征下所有的数据都为0,那么他就不具备,则删除该特征,达到降维的效果
- Embedded(嵌入式) :正则化、决策树
- Wrapper(包裹式)
代码实现(sklearn库)
from sklearn.feature_selection import VarianceThreshold
def var():
"""
特征选择-删除低方差的特征
:return: None
"""
var = VarianceThreshold(threshold=1.0) # threshold 指定方差的大小,删除所有低方差特征
data = var.fit_transform([[0, 2, 0, 3],
[0, 1, 4, 3],
[0, 1, 1, 3]])
# Variance.fit_transform(X,)
# X: numpy
# array格式的数据[n_samples, n_features]
# 返回值:训练集差异低于threshold的特征将被删除。
# 默认值是保留所有非零方差特征,即删除所有样本
# 中具有相同值的特征。
print(data)
return None
if __name__ == '__main__':
var()
输出:
[[0]
[4]
[1]]
主成分分析(Principal Component Analysis,PCA)
本质
PCA是一种分析、简化数据集的技术。
PCA就是把你的维度降低,但是依旧可以看出数据所体现的意思。
就如去给三维立体的水壶拍照,前三张照片【二维】都不能很好的体现出这是水壶,
但是最后一张却可以,但是它依旧是二维的,却可以很好的识别出,那是因为所保留的特征值足够或良好【这里的特征值是水壶应有的特征】

目的
是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
作用
可以削减回归分析或者聚类分析中特征的数量
适用
特征数量到达上百的时候
代码实现(sklearn库)
PCA(n_components=None) : 将数据分解为较低维数空间
n_components:一般两种形式
- 小数 0~1(百分比的形式) -----> 指定损失的信息量保留多少 通常保留90~95%
【保留30%这种也可以,但损失的信息就很多了,可能就只剩下一个特征,那么这样的话就无法通过该特征来识别目标值了(达不到最终目标)】 - 整数 -----> 减少到的特征数量【一般不用】
from sklearn.decomposition import PCA
def pca():
"""
主成分分析进行特征降维
:return: None
"""
pca = PCA(n_components=0.9)
# PCA.fit_transform(X)
# X: numpy
# array格式的数据[n_samples, n_features]
# 返回值:转换后指定维度的array
data = pca.fit_transform([[2, 8, 4, 5],
[6, 3, 0, 8],
[5, 4, 9, 1]])
print(data)
return None
if __name__ == "__main__":
pca()
输出:输出的是两个特征
[[ 1.22879107e-15 3.82970843e+00]
[ 5.74456265e+00 -1.91485422e+00]
[-5.74456265e+00 -1.91485422e+00]]
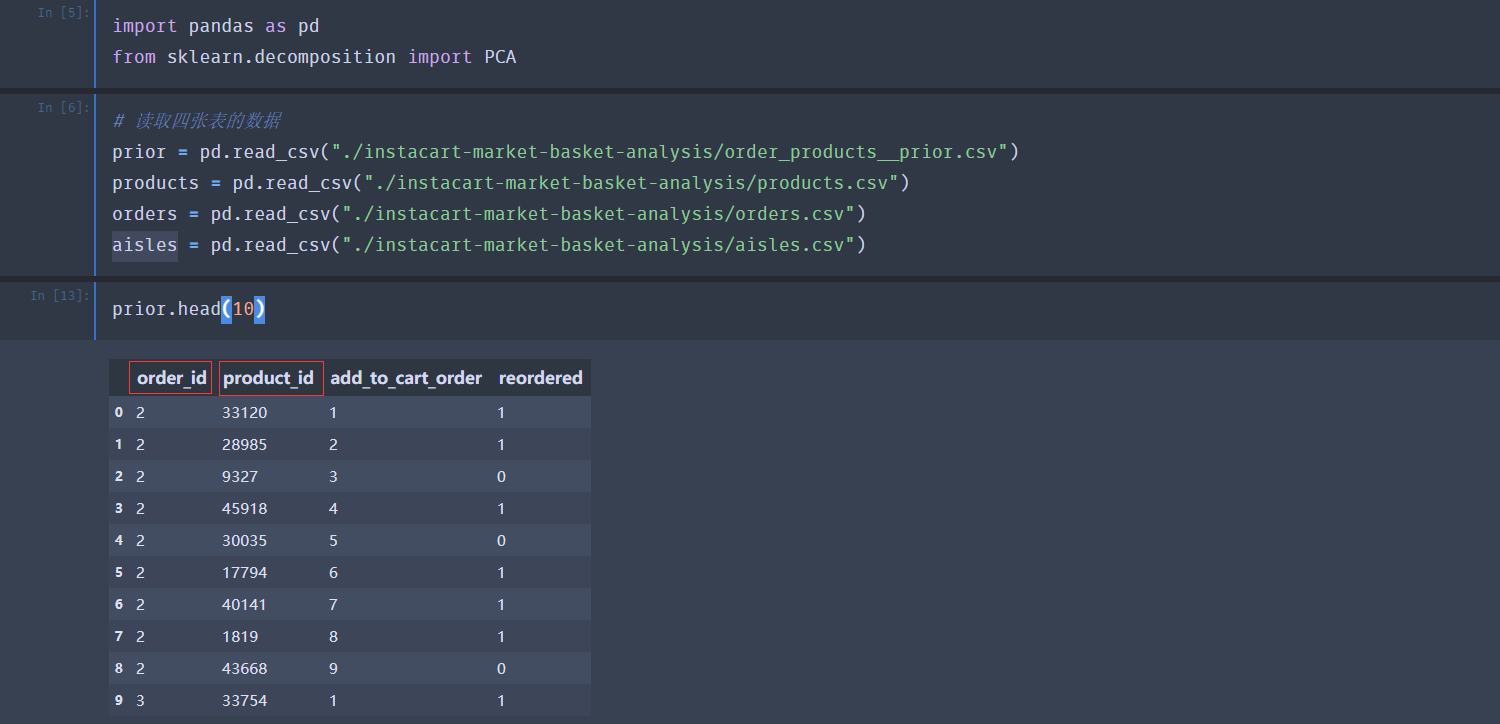
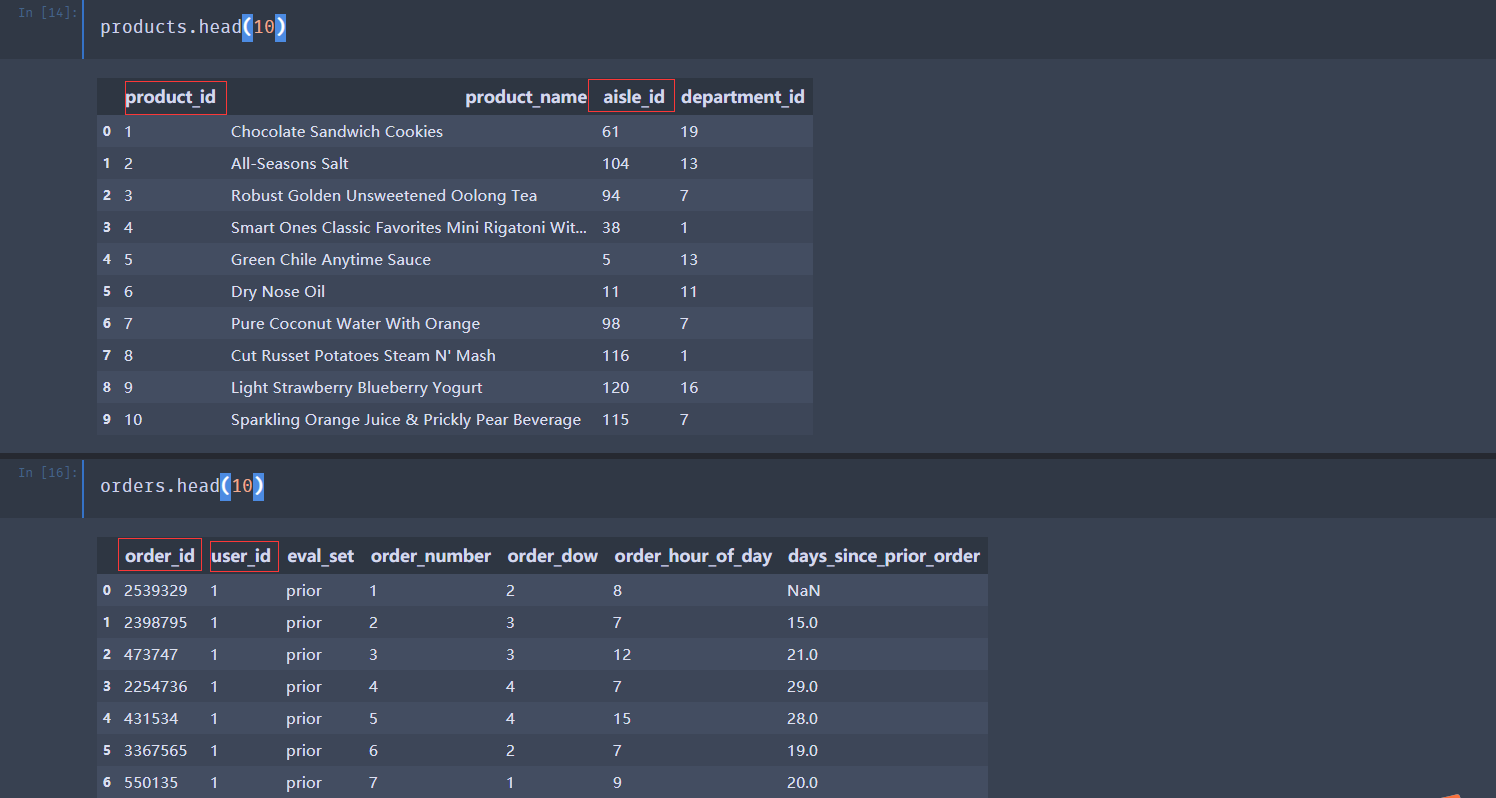
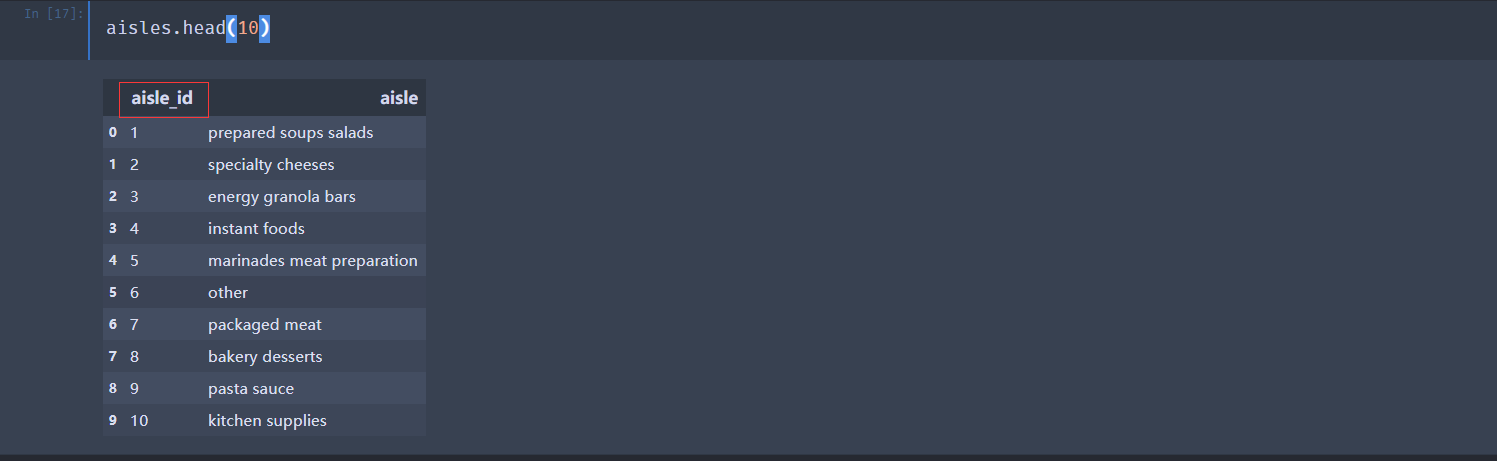
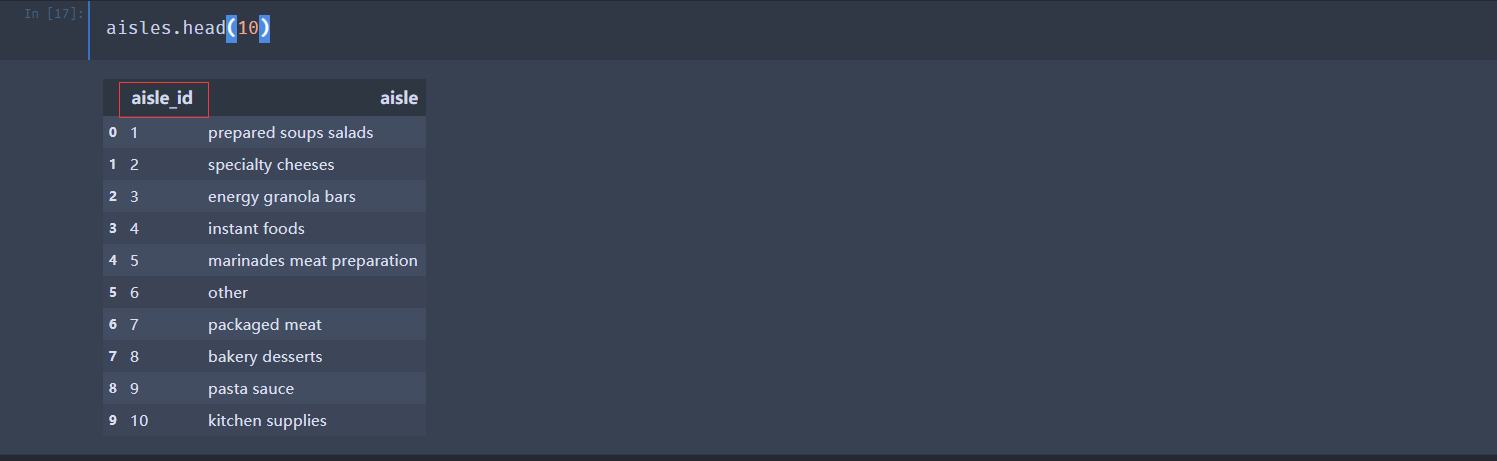
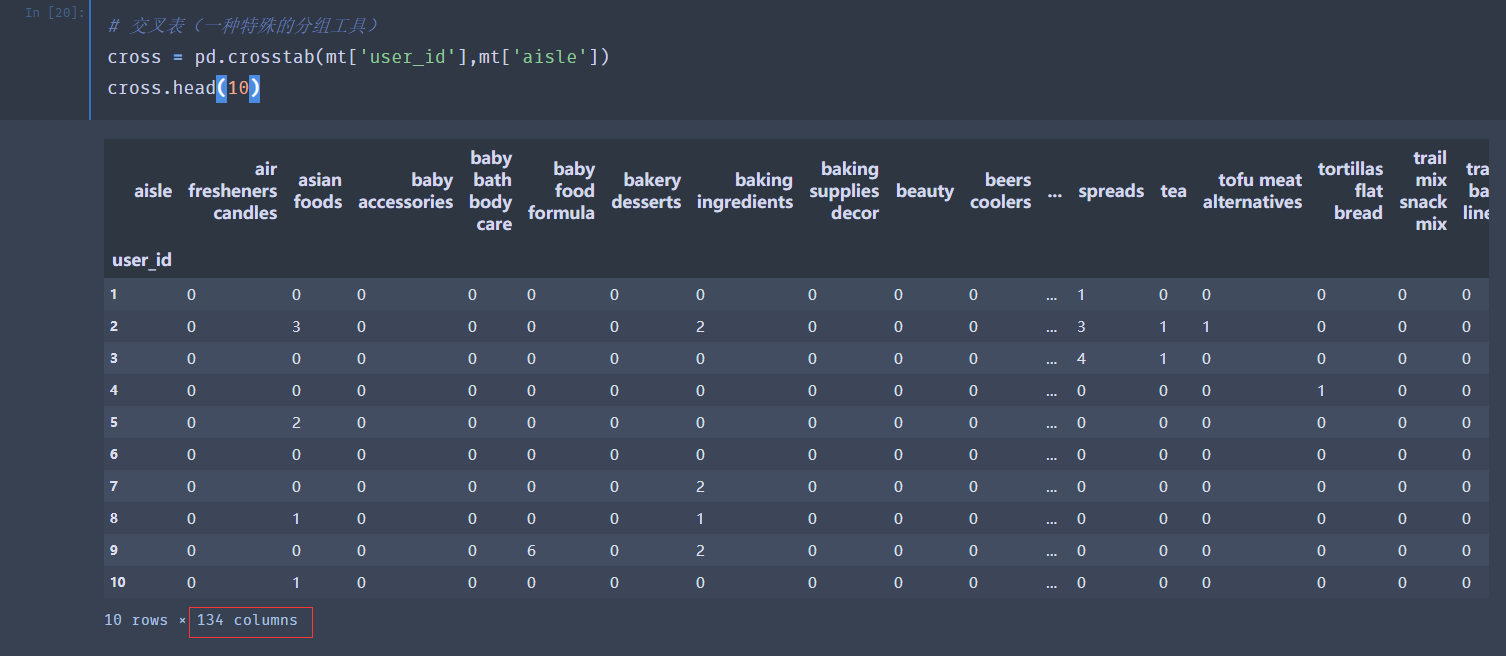
案例:用户对物品类别的喜好细分降维

Instacart Market Basket Analysis URL : https://www.kaggle.com/c/instacart-market-basket-analysis
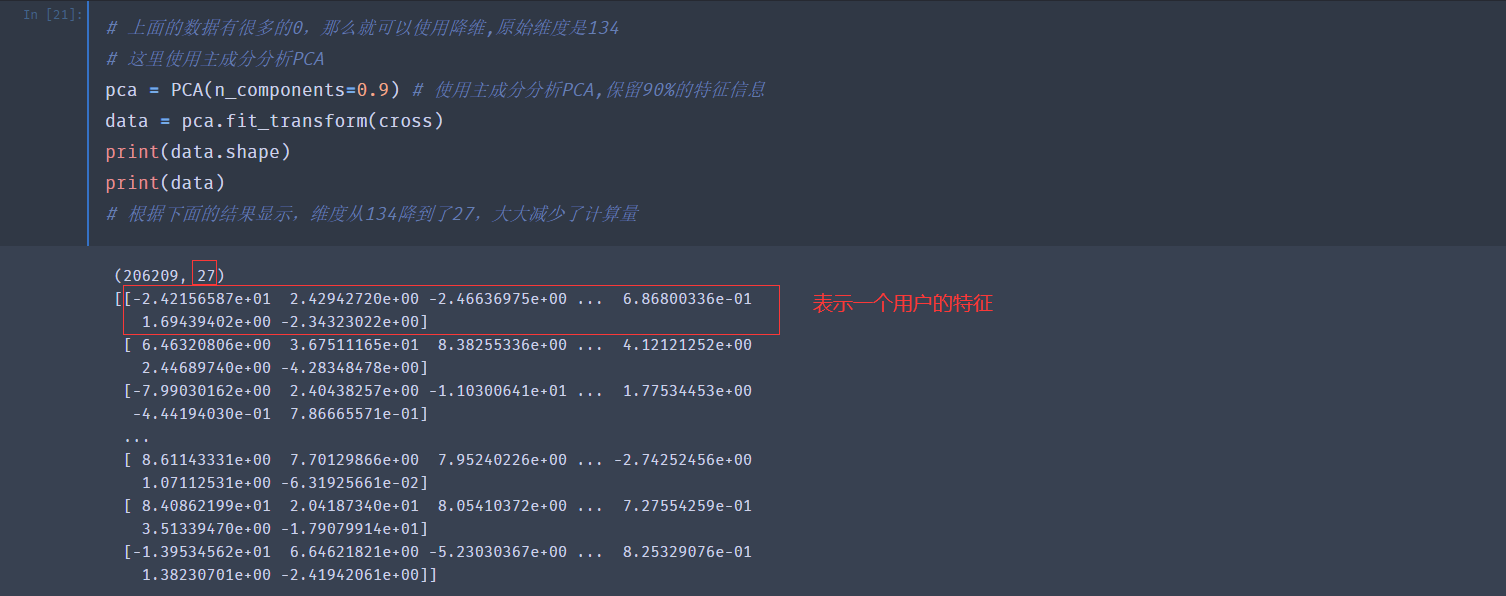
下面使用主成分分析PCA进行降维:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号