图论
哥尼斯堡的桥
图论——网络科学的数学基础。
图论起源于1735年的哥尼斯堡(Konigsberg)。作为东普鲁士的首府,哥尼斯堡在那个时代是一座繁荣的商业城市。由络绎不绝的商船支撑着的贸易,为哥尼斯堡带来了丰厚的经济收入。经费充足的市政府在环绕市区的普雷格尔河(Pregel)上建造了7座桥。普雷格尔河的两条支流将美丽的奈佛夫岛(Kneiphof)和大陆隔开,奈佛夫岛和大陆通过5座桥相连。另外的两座桥分别修建在普雷格尔河的两条支流上。如此独特的城市布局给哥尼斯堡人带来了一个时代难题:能否不重复地走过每座桥?人们做了很多次尝试,却始终没有找到这样的路径。这个问题一直无人能解,直到1735年,出生于瑞士的数学家莱昂哈德·欧拉(Leonhard Euler)才对此做出了严格的数学证明:不存在这样的路径。
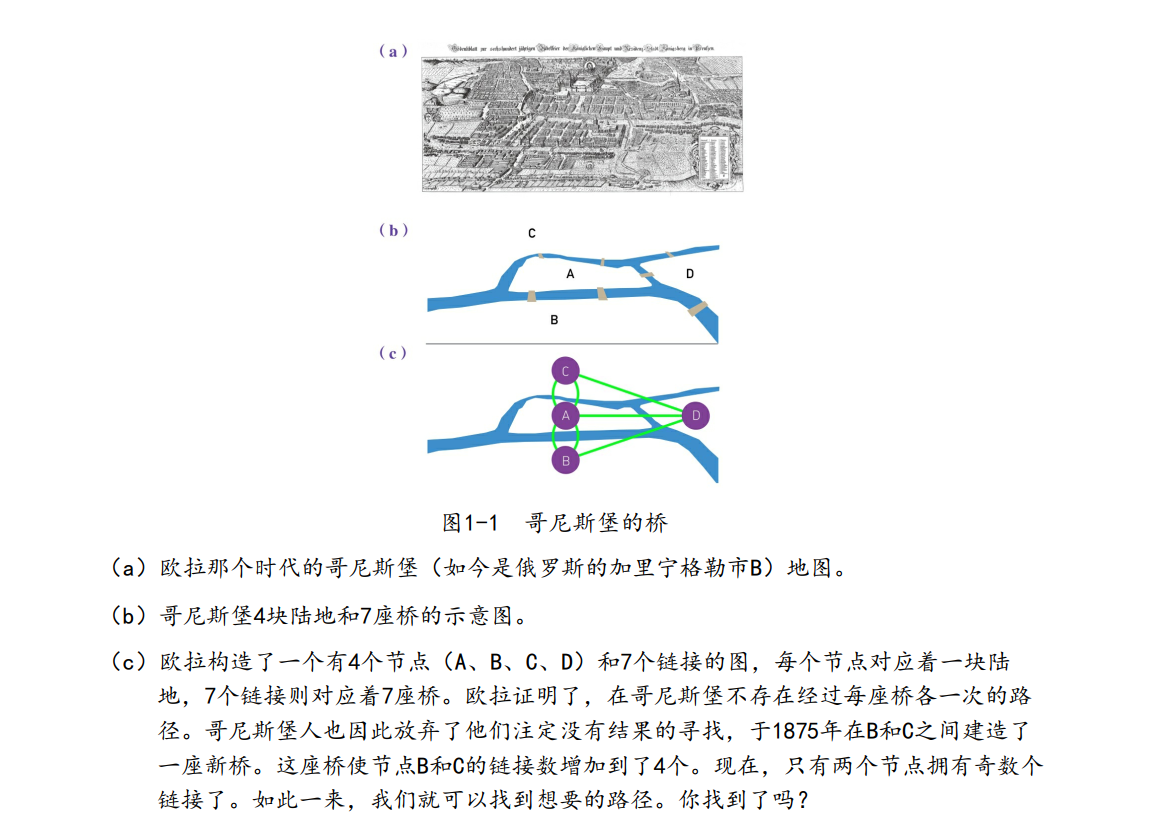
用抽象的点和线构成的图来表示实际网络,可能会丢失实际网络的许多特性,但是前提是这些信息丝毫不影响问题的求解,这体现了科学研究中的一个基本的建模原则:能够解决问题的最简单的模型就是最好的模型。
经过每座桥各一次的路径只能有一个起点和一个终点。
因此,如果一幅图中拥有奇数个链接的节点超过了2个,那么图中就不存在这样的路径。哥尼斯堡七桥所对应的图中,拥有奇数个链接的节点有4个,分别是A、B、C和D,因此不存在满足要求的路径。
欧拉的证明第一次使用了图来求解数学问题。这一证明给我们带来了两点启示:
首先,有些问题在使用图进行表示时会变得简单起来,且更容易求解;
其次,路径的存在性是图的一种性质,不取决于我们是否能够找出这样的路径。
实际上,在哥尼斯堡图结构已知的情况下,无论我们多么聪明,都无法找到想要的路径。换句话说,网络的某些性质是编码在其结构中的,网络性质和其结构密切相关。
网络和图
网路与图的区别
人们很少会对其进行区分,因此这些术语经常被作为同义词使用,但是也有细微的差别:
-
“网络、节点、链接”这个组合通常用于表示真实的系统:
万维网是网页之间的网络,社会是个体间通过家庭、朋友、职业纽带等连接起来的网络;代谢网络是细胞内发生的所有化学反应的总和。
-
“图、顶点、边”则经常在讨论这些网络的数学表示时使用:
万维网图、社会关系图(因Facebook而流行起来的一个词)或代谢关系图。
网络中的点通常称为节点(Node),图中的点则常称为顶点(Vertex)。
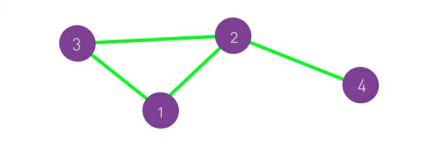
节点数N,表示系统中组成部分的个数。我们通常将N称为网络大小。为便于区分,网络中的各个节点记为i=1 , 2 , …,N。
链接数L,表示节点间交互关系的总数。一般而言,我们很少对链接直接进行标记,而是通过其连接的两个节点来标记。例如,(2,4)表示连接节点2和节点4的链接。
上图中的网络,节点数和链接数均为4。
有向网络
如果一个网络中所有的链接都是有向的,我们称之为有向网络或有向图。
例如,万维网中的链接由一个网页指向另一个网页;手机通话网络中的链接由呼叫者指向被呼叫者。
无向网络
如果其所有链接都是无向的,我们称之为无向网络。
例如,恋爱关系网络中,恋爱双方之间的关系是无向的;电网中的传输线是无向的,电流可以沿着两个方向流动。
其他网络
还有一些网络同时包含有向的链接和无向的链接。
例如,在代谢关系网络中,有些代谢关系是可逆的——对应无向的链接,有些代谢关系是不可逆的——对应有向的链接。
简单图
在图论中,没有重边和自环的图称为简单图(Simple graph)。
网络中没有重边( Multi-edge) ,即任意两个节点之间至多只有一条边。
没有自环( Self-edge ),即没有以同一个顶点为起点和终点的边。
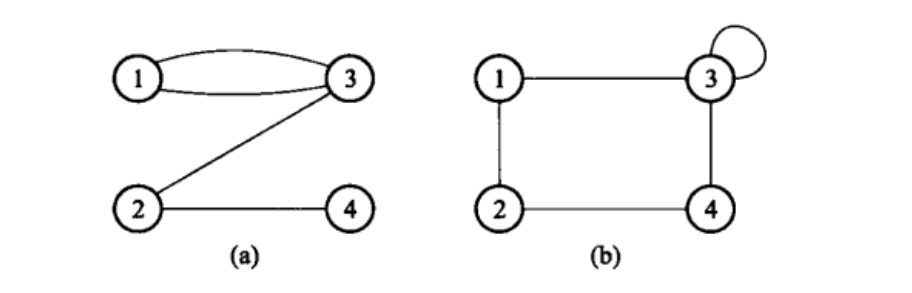
图(a)中顶点1和顶点3之间有重边,图(b)中顶点3有自环,因此这两个图都不是简单图。
简单图的两种极端情形为:
- (1)空图(Null graph):它有两种定义,一是指没有任何节点和连边的图;二是指没有任何连边的图,即由一群孤立节点组成的图。
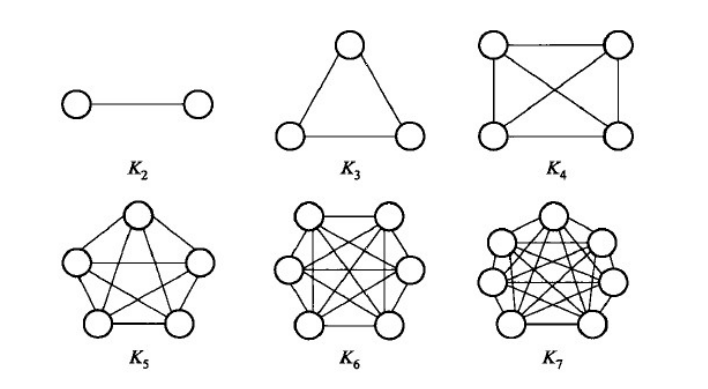
- (2)完全图(Complete graph)\(K_N\):图中任意两个顶点之间都有一条边,即总边数为 N(N - 1)/2。
这里的K是以波兰图论专家Kuratowski (1896—1980)命名。下图给出了几个小规模的完全图的例子。
度、平均度和度分布
度
度是节点的一个关键属性,表示该节点和其他节点之间的链接个数。
例如:在手机通话网络中,度表示一个人通过手机联系过的人数;在引文网络中,度表示一篇论文获得的引用数。

我们使用 $k_i $ 表示网络中第\(i\)个节点的度。例如,对于上图所示的无向网络,我们有\(k_1\)=2,\(k_2\)=3,\(k_3\)=2,\(k_4\)=1。在无向网络中,总链接数\(L\)可以使用节点度之和来表示:
在计算节点度之和时,每个链接被计算了两次,因此公式中有一个系数1/2。
例如,在上图中,连接节点2和节点4的链接,在计算节点2的度时被计算了一次,在计算节点4的度时又被计算了一次。
平均度
平均度是网络的一个重要属性。
在无向网络,平均度被定义为:
在有向网络中,需要区分入度和出度。
入度 \(K_i^{in}\),表示指向节点 \(i\) 的链接个数。
出度 \(K_i^{out}\);表示节点 \(i\)指向其他节点的链接个数。
从而,节点 \(i\) 的度为:
例如,在万维网中,网页的出度 \(K_i^{out}\)表示该网页指向的网页数目,其入度\(K_i^{in}\)表示指向它的网页数目。有向网络中的总链接数为:
有向网络的平均度为:【L表示节点度之和,N表示总节点数】
度分布
度分布\(P_k\),表示“网络中随机选出的一个节点其度为\(K\)”的概率。由于\(P_k\)是一个概率,则其必须满足归一化约束,即:
这里的\(N_k\),是指度为k的节点个数,N表示总节点数。因此,度为k的节点个数可以根据度分布计算出来,即\(N_k\)=N\(P_k\)
案例:
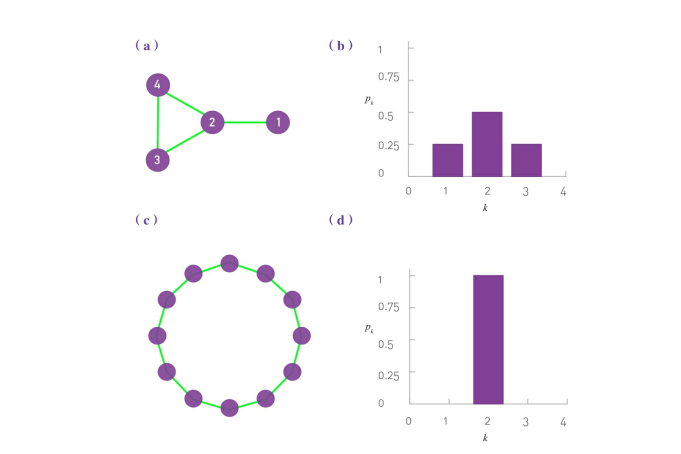
(1)网络a的网络大小为N=4,其度分布如图b所示。【L表示节点度之和,N表示总节点数】
(2)网络a一共4个节点:
有1个度为1的节点(\(K_1\) = 1),因此 \(P_1\)=1/4
有2个度为2的节点(\(K_3\) = \(K_4\) = 2),因此 \(P_2\)=1/2
有1个度为3的节点(\(K_2\) = 3),因此 \(P_3\)=1/4
没有度大于3的节点,因此,对于任意K>3,我们有\(P_k\) = 0
(4)对于一维格子网络而言,所有节点的度都是2。
(5)图c所示网络的度分布是克罗内克(Kronecker)的德尔塔函数,即\(P_k\)= δ(k-2)。
度分布被认为在网络科学中发挥了核心作用,特别是在无标度网络被发现之后。其中一个原因是,大多数网络性质可以通过度分布计算得到。例如,网络平均度可以写成:
另一个原因是,度分布的具体函数形式决定着很多网络现象,例如网络健壮性和病毒传播。
接下来,让我们看一看真实网络中有着怎样的度分布【真实网络中,节点的度差异很大】。
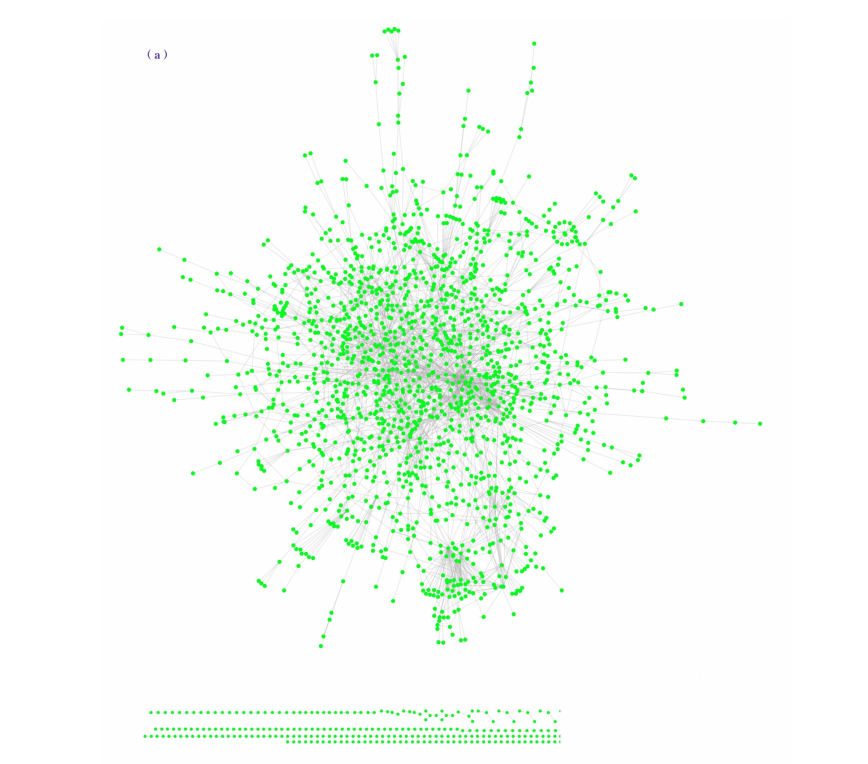
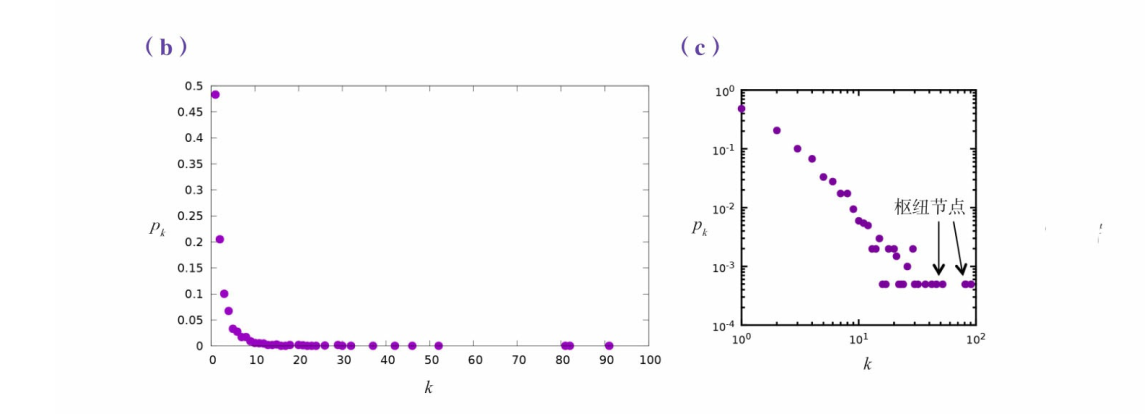
图a所示的蛋白质相互作用网络的度分布。节点的度分布在0(对应孤立节点)和92(对应度最大的那个节点,此类节点通常被称为枢纽节点)之间。度不同的节点,其个数也差异很大:度为1的节点有几乎一半(\(P_1\)=0.48),而只有一个节点的度为92(\(P_{92}\)=1/N=0.000 5)。
例如:假设有一个蛋白质网络是一个无向网络,有N=2018个蛋白质作为节点,L=2 930个交互关系作为链接。因此,根据公式,该网络的平均度为
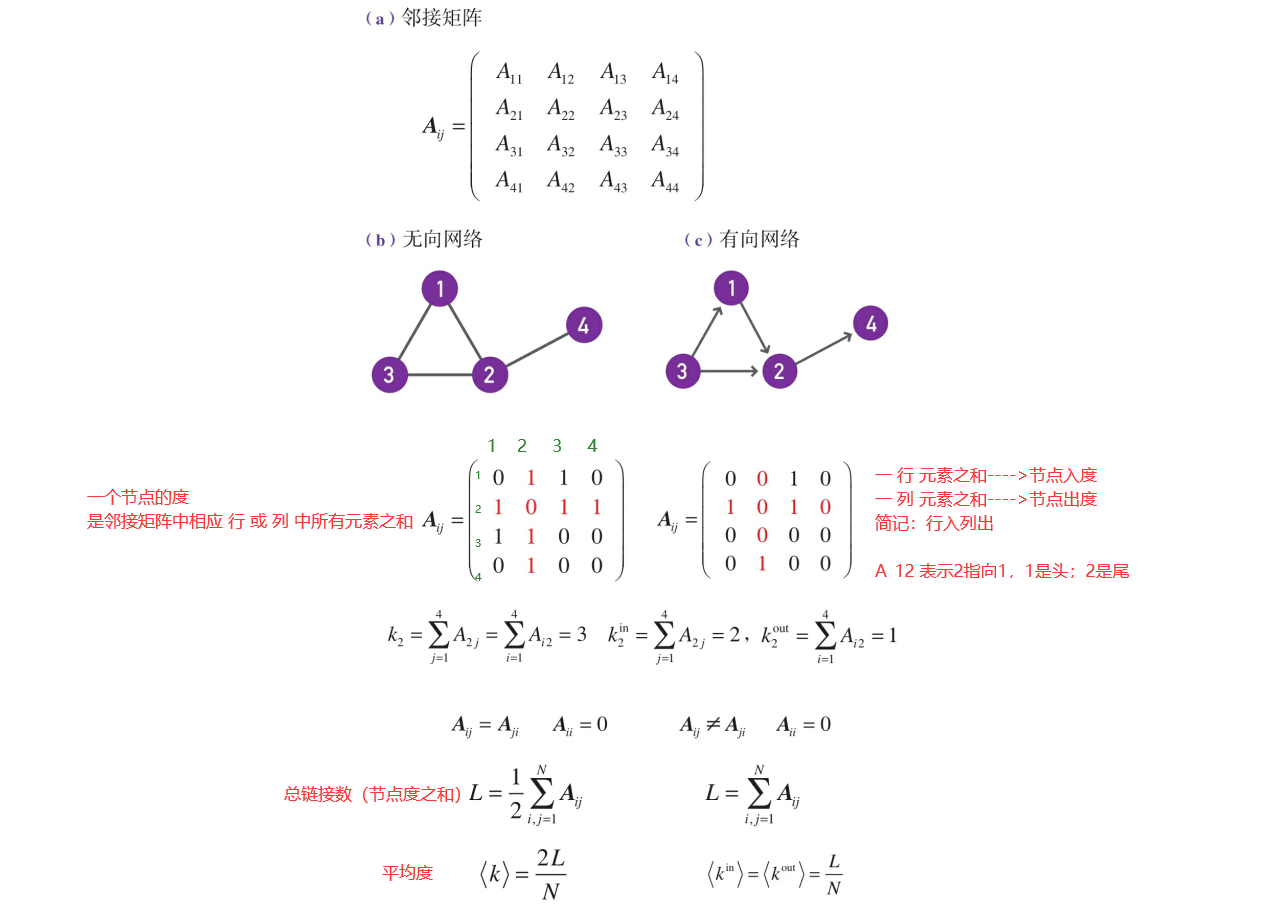
邻接矩阵
从数学角度考虑,我们经常使用邻接矩阵来表示网络。
一个拥有N个节点的有向网络,其邻接矩阵有N行N列。邻接矩阵的元素定义如下:
如果存在一个链接从节点 j 指向节点 i ,则\(A_{ij}\)=1;如果节点 i 和节点 j 彼此不相连,则\(A_{ij}\)=0。
对于无向网络,每个链接对应邻接矩阵中的两个元素【无向网络的邻接矩阵中非零元素个数为2L,即链接个数的2倍。】。例如,链接(1,2)对应着\(A_{12}\)=1和\(A_{21}\),=1。因此,无向网络的邻接矩阵是对称的,即\(A_{ij}\)=\(A_{ji}\)。
真实网络是稀疏的
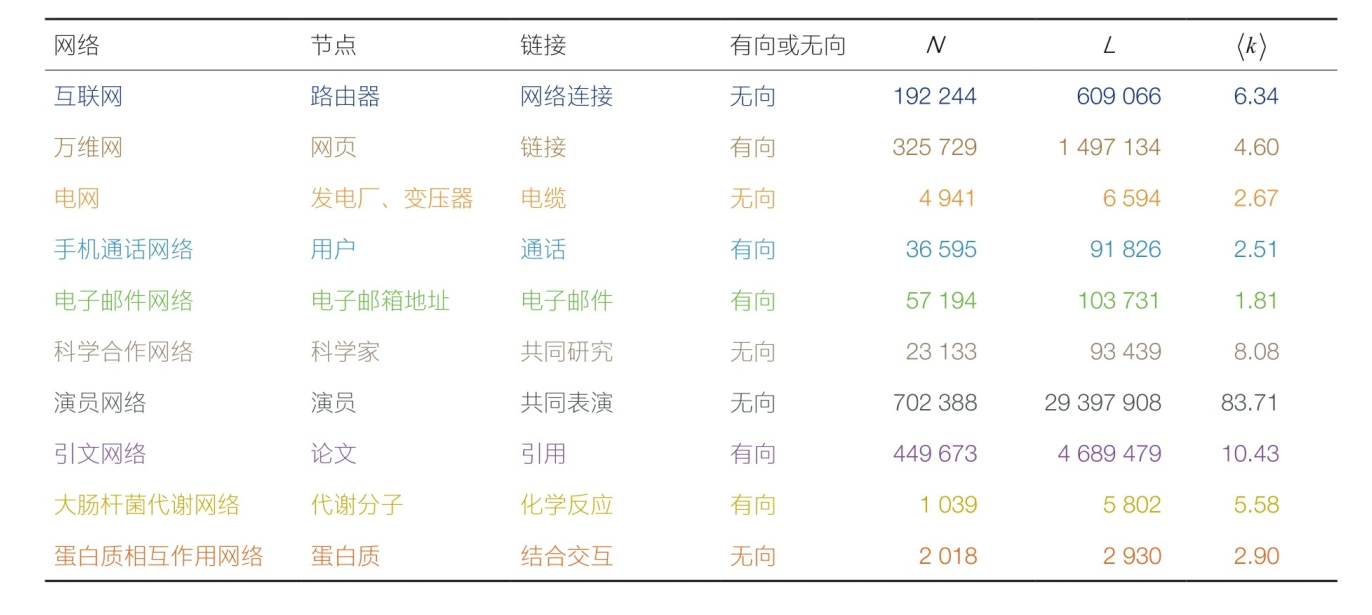
网络大小上的巨大差异可以从上表中明显看出。表列出了一些网络的节点数和链接数。有些网络是其所描述系统的完整连接关系,例如演员关系网络和秀丽隐杆线虫的神经元网络;而其他网络则只是整个网络的一部分,例如万维网和手机通话网络。
从理论上讲,对于拥有N个节点的无向网络,其链接数最小为L=0,最大为\(L_{max}\)。其中:
表示大小为N的完全图包含的链接总数。在完全图中,任意两个节点之间都有链接相连。例如:如下图(一个完全图),包含N=16个节点的完全节点,根据上述公式,其链接数为\(L_{max}\)=120
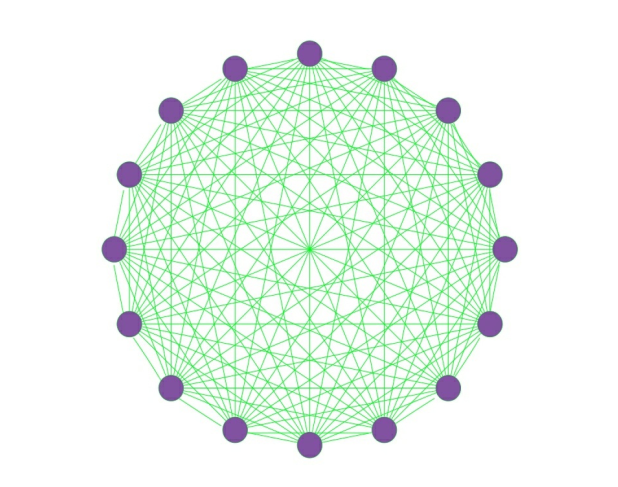
真实网络中,L远小于\(L_{max}\),说明大部分真实网络是稀疏的。
当L\(<<\)\(L_{max}\)时,我们说该网络是稀疏的。例如,上表中的万维网包含大约150万个链接。不过,如果该万维网是完全图,根据公式,它应该有\(L_{max}\)≈5×\(10^10\)个链接。也就是说,万维网实际包含的链接数占最大可能链接数的比例仅为3×\(10^-5\)。实际上,表中的所有网络都是稀疏的:实际链接数相对于最大可能链接数(具有同样节点数的完全图所包含的链接数)只占很小一部分比例。
真实网络的稀疏性意味着其邻接矩阵也是稀疏的。
真实网络的邻接矩阵中,只有很小一部分元素非零。
加权网络
在许多应用中,我们需要研究加权网络,令科学界感兴趣的大多数网络都是加权网络。加权网络中的每个链接\((i , j)\)都有自己的权重\(w_j\)。
例如在手机通话网络中,权重可以表示两个人之间手机通话的时长(例如分钟数);在电网中,权重可以表示传输线路上流过的电流量。
对于加权网络而言,邻接矩阵的元素表示链接的权重,即
梅特卡夫定律:网络的价值
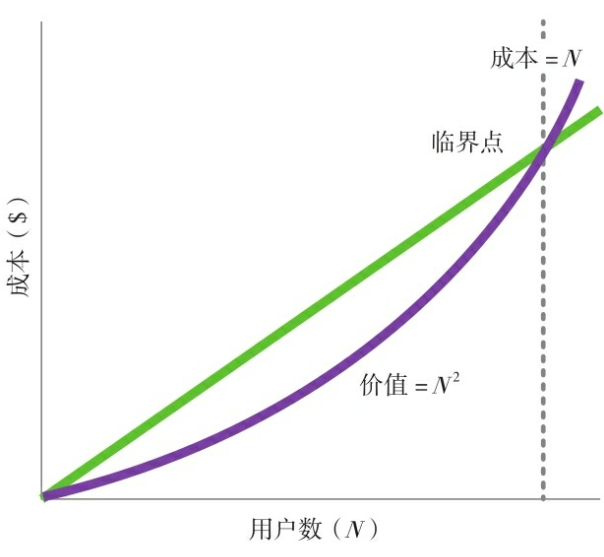
梅特卡夫定律指出,网络的价值与网络节点个数的平方(\(N^2\))成正比。
该定律是罗伯特·梅特卡夫 (Robert M. Metcalfe)在1980年左右阐述通信设备网络价值时提出的。梅特卡夫定律背后的思想是,网络用户数越多,网络就越有价值。例如,你的朋友中使用电子邮件的人越多,电子邮件这项服务对你而言就越有价值。
20世纪90年代后期互联网泡沫期间,梅特卡夫定律经常被用于对互联网公司进行定量估值。梅特卡夫定律表明,一项互联网服务的价值和其能创造的链接数成正比,也就是和其用户数的平方成正比。相比而言,其成本和用户数(N)却只是线性相关。因此,对互联网服务而言,只要能够吸引足够多的用户,就一定能够赢利,随着N的增加,\(N^2\)总会超过N(如下图)。梅特卡夫定律营造了“有服务就不愁用户”的心态,支撑着“增长必将带来利润”的信念。
对于拥有N个用户的通信网络,如果其每个链接的价值都是一样的,则网络总价值正比于\(\frac{N(N-1)}{2}\),大致为\(N^2\)。如果一个网络有N=10个用户,那么这些用户之间最多有\(L_{max}\)=45个不同的链接。
但是,有两个问题限制了梅特卡夫定律的有效性:
(1) 大多数网络是稀疏的,这意味着只有很小一部分链接会出现。因此,网络价值并非像\(N^2\)那样增大,而是与网络大小N呈线性关系。
(2) 链接是有权重的,并不是所有链接的价值都一样。有些链接经常被使用,而绝大多数链接很少被使用。
二分网络
二分网络(或二分图)是这样一种网络:其节点可以分成两个不相交的节点集合U和V,使得每个链接都连接着一个U中的节点和一个V中的节点。换句话说,如果我们把集合U中的节点涂成绿色,把集合V中的节点涂成紫色,则每个链接连接着颜色不同的两个节点。
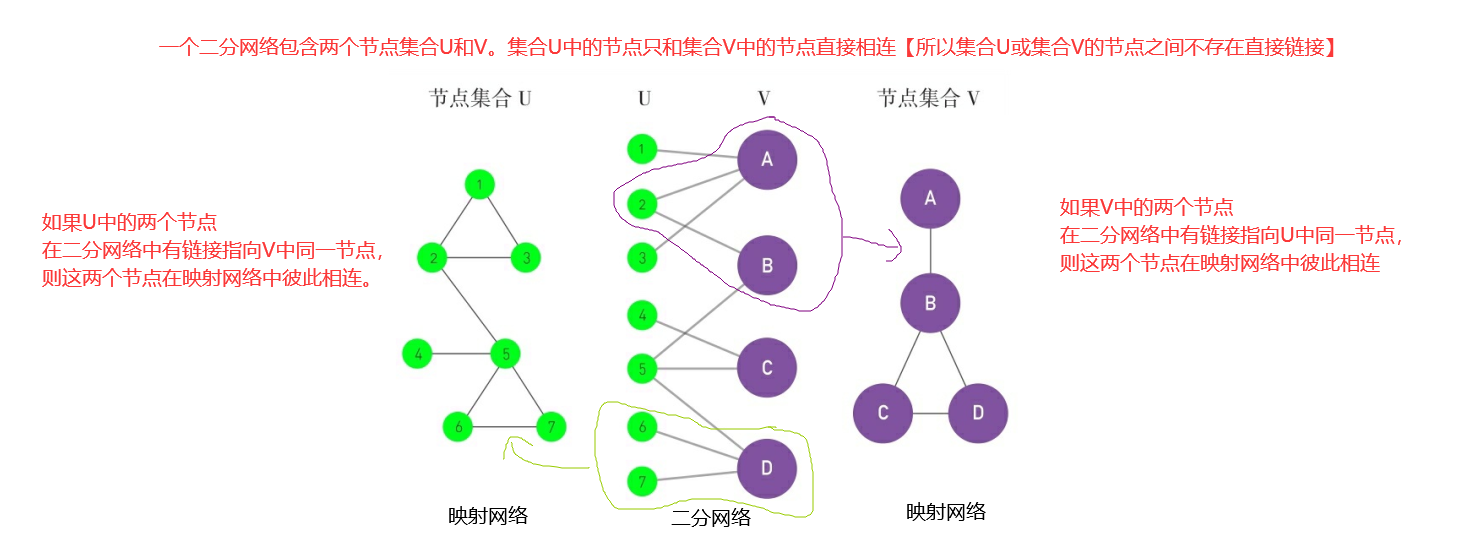
网络科学研究中,我们会碰到很多二分网络。一个著名的例子是好莱坞电影演员网络,其中一个节点集合对应着电影(记为U),另一个节点集合对应着演员(记为V)。如果某个演员出演了某部电影,则二者之间有一个链接。该二分网络的一个映射网络是演员网络——出演过同一部电影的两个演员之间彼此相连。另一个映射网络是电影网络——至少有一个演员相同的两部电影彼此相连。
路径和距离
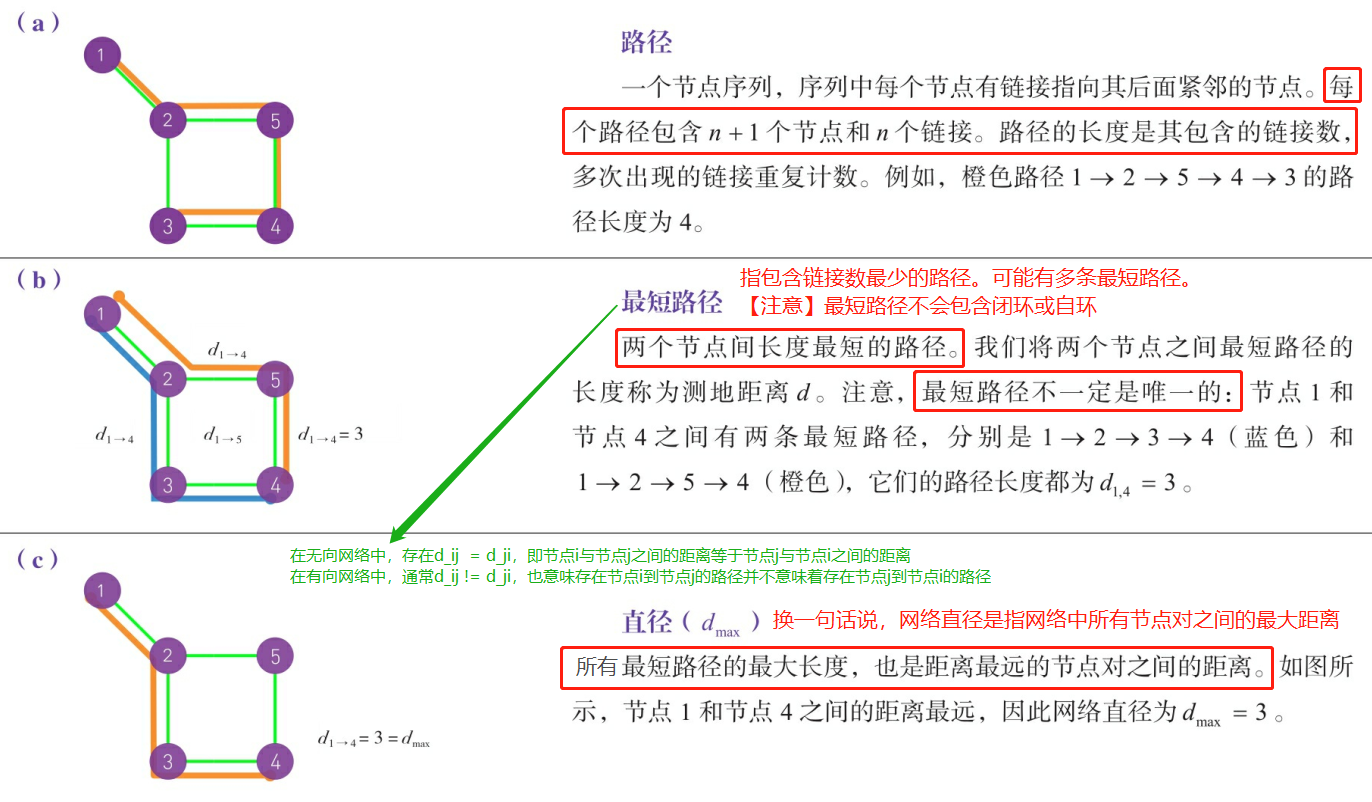


连通性
手机作为一种通信设备,如果不能呼叫任何有效的手机号码,其用途就非常有限了;电子邮箱如果只能给少数几个邮件地址发邮件,也就没有多大用处了。
从网络的角度看,这意味着手机或互联网背后的网络必须能够在任意两个节点之间建立一条路径。实际上,这是大多数网络的关键效用——确保连通性。
无向网络中,如果节点 i 和节点 j 之间存在一条路径,则它们是连通的。如果不存在路径(\(d_∞\)),则它们是不连通的。
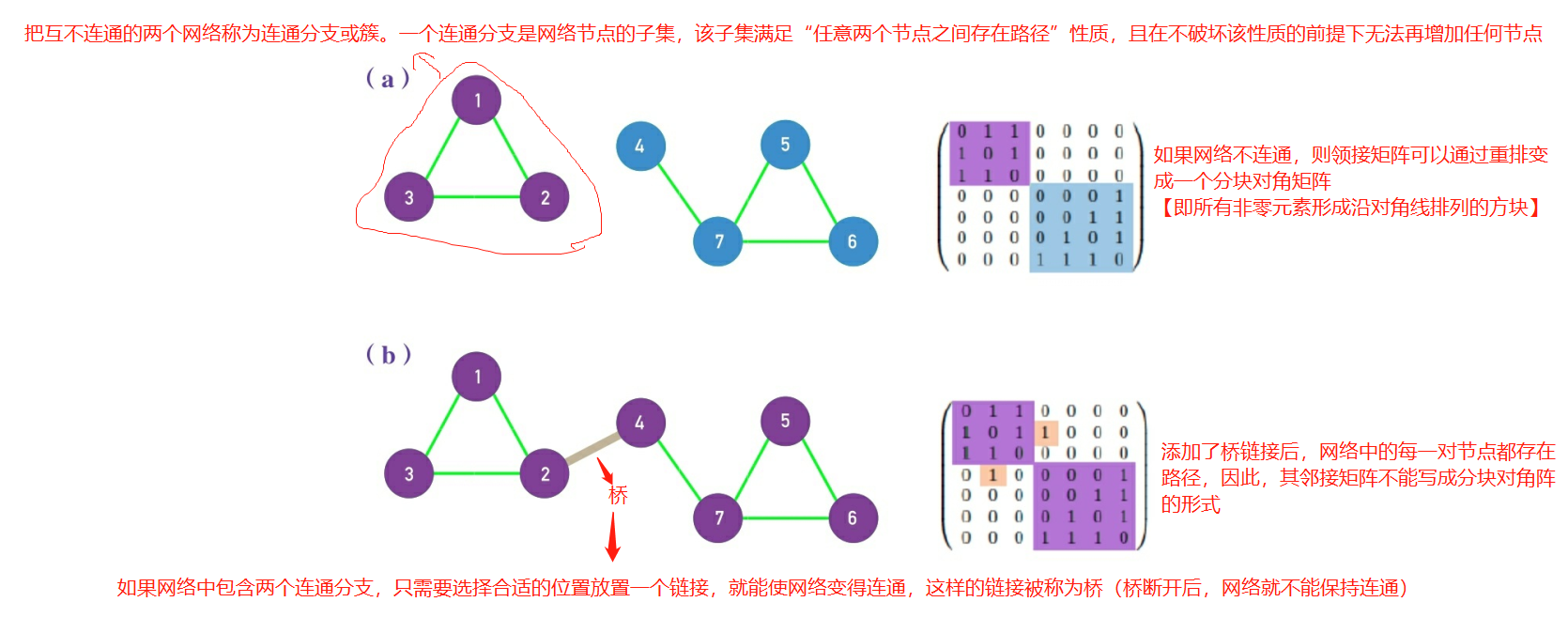
如果一个网络的所有节点对都是连通的,我们说该网络是连通的。如果网络中至少有一对节点是不连通的,则该网络是不连通的。
集聚系数
集聚系数刻画了一个节点的邻居节点之间彼此连接的稠密程度。
例如:
在你的朋友关系网络中,你的两个朋友很可能彼此也是朋友,这种可能性的大小反映了你的朋友圈的紧密程度。
我们可以用你的聚类系数(Clustering coefficient)来定量刻画你的任意两个朋友之间也互为朋友的概率。
国内对Clustering coefficient也有译为簇系数、集聚系数或群集系数。
对于一个度为 \(K_i\) 的节点 i ,其局部集聚系数定义为:
其中\(L_i\)表示与节点 i 直接相连接的节点(邻居节点)之间的链接数。\(K_i\)表示节点 i 与邻居节点的链接数。
注意:聚集系数的取值介于0到1之间【注意,对于度为0或1的节点,集聚系数为0。】。
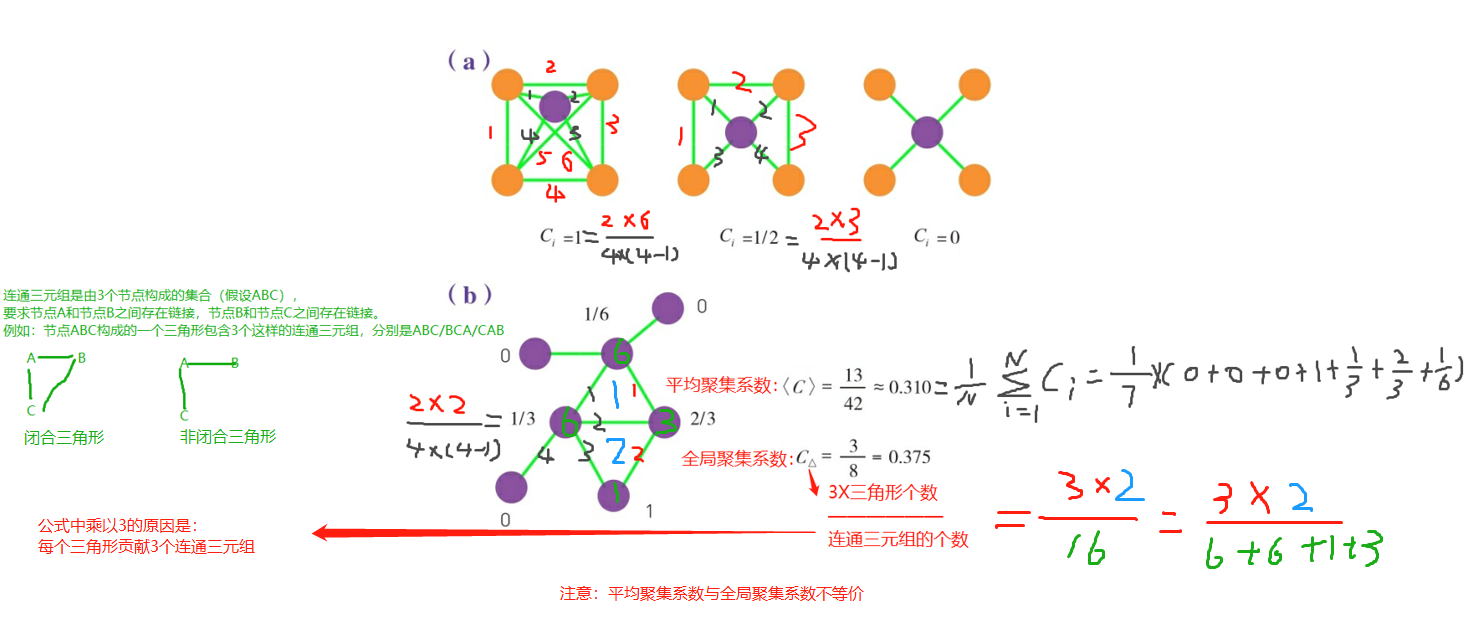
\(C_i\)=O表示节点i的所有邻居彼此都不相连。
\(C_i\)=1表示节点 i 的所有邻居形成了一个完全图,即邻居两两相连。
\(C_i\)表示节点 i 的任意两个邻居彼此相连的概率。因此,\(C_i\)=0.5意味着节点i的任意两个邻居有50%的概率彼此相连。
整个网络(无向网络)的集聚程度可以通过其所有节点的平均集聚系数
平均集聚系数
可以从另一个角度来阐述节点 i 的聚类系数的定义。
\(E_i\)也可看做是以节点 i 为顶点之一的三角形的数目。
因为节点 i 只有 k 个邻节点,包含节点 i 的三角形至多可能有\(K_i(K_i-1)/2\)个。
如果用以节点 i 为中心的<>b连通三元组表示包括节点 i 的 3 个节点,并且至少存在从节点 i 到其他两个节点的两条边
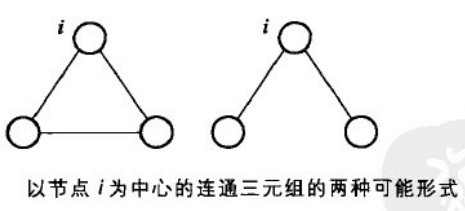
三角形的社会学意义是你的两位朋友也互相为朋友,从而3人之间形成一个三角形。因此,在社会学中是用网络中三角形的相对数量来刻画网络的聚类特性,也称横截性( Transitivity)。
那么以节点 i 为中心的连通三元组的数目实际上就是包含节点 i 的三角形的最大可能的数目,即\(K_i(K_i-1)/2\)。
因此,我们可以给出与定义等价的节点 i 的聚类系数的几何定义如下:
举例:
考虑下图所示的包含6个节点的网络。
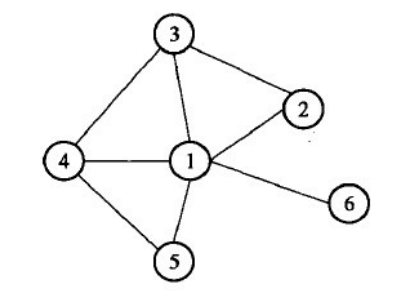
对于节点1有\(L_1\)=3,\(K_i\) = 5,于是有
同理
于是整个网络的聚类系数为
其他


注意,很多真实网络可以同时具备这些基本性质中的多个。例如,万维网是带自环的无向多重图;手机通话网络是有向加权无自环的网络。
参考:
[1] [美] Albert-László Barabási.巴拉巴西网络科学[M].沈华伟,等,译.河南:河南科学技术出版社,2020
[2] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012


 浙公网安备 33010602011771号
浙公网安备 33010602011771号