推荐系统(recommender systems):预测电影评分--构造推荐系统的一种方法：基于内容的推荐

如何对电影进行打分:根据用户向量与电影向量的内积

我们假设每部电影有两个features,x1与x2。x1表示这部电影属于爱情片的程度，x2表示这部电影是动作片的程度，如Romance forever里面x1为1.0（说明电影大部分为爱情），x2=0.01(说明里面有一点动作场面)。

还是像以前一样加上一个额外的截距特征变量x₀=1，这样第一部电影（love at last）表示为x⁽¹⁾=[1,0.9,0]^T，上标(1)表示为第一部电影

我们仍用n表示特征变量的数量，在这个例子中n=2,有2个特征(x1,x2,不包括x0)

将每个观众当成一个独立的线性回归问题，每一个用户j，我们都学习出一个参数θ^(j)为一个三维向量（更一般θ^(j)为一个n+1维向量，n为特征数量的个数,+1是因为θ0）,我们根据θ^(j)与x(i)(例子中为3维向量，表示电影的特征)的内积来预测用户j对电影i的评分

例子：如用户1对应的参数向量θ⁽¹⁾,每个用户都有一个不同的参数向量,现在我们想预测Alice对电影3的评价，x⁽³⁾=[1,0.99,0],假如对于这个例子，我们已经知道了θ⁽¹⁾的值（后面会讲到这个参数值是怎么得到的），现在假设我们已经算出了θ⁽¹⁾的值=[0,5,0]^T,求θ⁽¹⁾与x⁽³⁾的内积得到4.95,表示用户1(Alice)对电影3的评价打分是4.95.

我们对每个用户应用不同的线性回归模型，来预测他对某部电影的评分

基于内容推荐问题的描述

 

m(j)表示用户j评价过的电影数量,为了学习参数向量θ(j)(表示用户j的参数向量),一个线性回归问题，选择一个θ(j)，使得预测结果即θ(j)与x(i)的内积接近于我们在训练集中的观测值。

即求出使代价函数最小的θ(j)的值。

i:r(i,j)=1,表示对于满足所有r(i,j)=1上的i求和，即是对用户j打过分的所有的电影预测值与实际值之间的差的平方求和，后面是正则化项（对θ0没有进行正则化，因为θ0表示常数项）

θ^(j)是一个n+1维的向量，其中n表示电影的特征数

为了更简单，我们将m(j)这项去掉，为一个常数，去掉它并不会影响当我的函数值取最小值时--我的θ(j)的取值

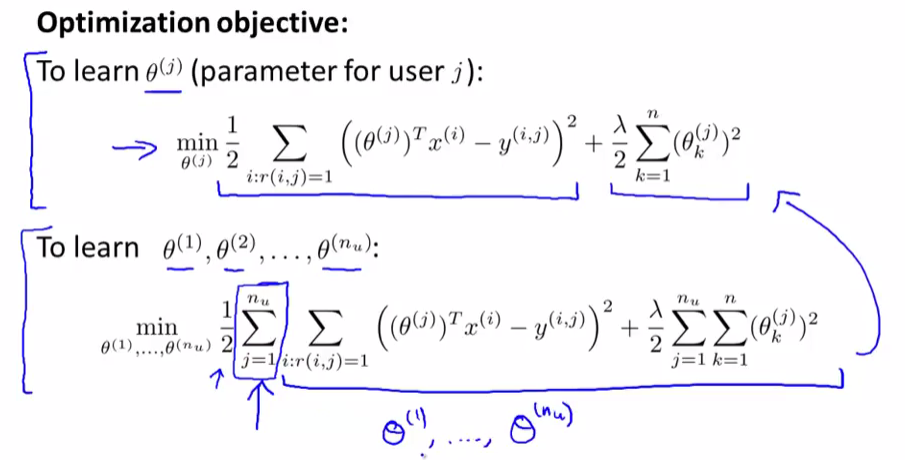
上面的式子是对单个用户j求它的最小值，求出其参数θ^(j)

为了求多个用户n_u个用户，我们对用户进行累加从1到n_u进行累加，然后求取最小值时的参数θ(1)，θ(2)...,θ(n_u)时的取值

最小化代价函数J(θ(1)......θ(n_u))

梯度下降法求参数，其中α为学习率，对于k=0与k不等于0的情况的公式不同，因为我们没有对θ₀进行正则化。

与之前线性回归不同的是少了1/m，因为我们在推导过程中将1/m消去了。

 总结

1>基于内容的推荐：预测不同用户对不同电影的评分。（基于内容:我们假设我们有不同电影的特征，如电影爱情成份为多少，动作成份为多少，利用电影的这些特征来进行预测）