machine learning- linear regression with one variable(2)
- Linear regression with one variable = univariate linear regression: 由一个输入变量预测出一个output (regression problem预测连续的值). single input<--->single output
- training set: 机器进行学习的元素集

- univariate linear regression = Linear regression with one variable
![]()
-
The Hypothesis Function(for linear regression):
![]() ,这是一个关于x的函数(θ0与θ1是固定的).这是一个假设的函数(求出假设的 θ0 和 θ1,这个是我们的目标,愈近的接近真实的y值),这样可以根据input value(x)来计算output value(y)
,这是一个关于x的函数(θ0与θ1是固定的).这是一个假设的函数(求出假设的 θ0 和 θ1,这个是我们的目标,愈近的接近真实的y值),这样可以根据input value(x)来计算output value(y) -
Cost Function(for linear regression):
![]() (y为真实的值),这是一个关于θ1与θ2(parameters)的函数,用来衡量假设函数(hypothesis function)的准确性,目的是选择使cost function最小的θ1与θ2的值,这样就能确定假设函数(Hypothesis Function)了.
(y为真实的值),这是一个关于θ1与θ2(parameters)的函数,用来衡量假设函数(hypothesis function)的准确性,目的是选择使cost function最小的θ1与θ2的值,这样就能确定假设函数(Hypothesis Function)了.- 图片
![]()
- 图片
- Squared error function = cost function
- Mean squared error = cost function
-
Gradient Descent: 一种用来自动提高hypothesis function准确性的方法,使cost function取最小值(不仅适用于linear regression,可用于整个机器学习).
-
图片
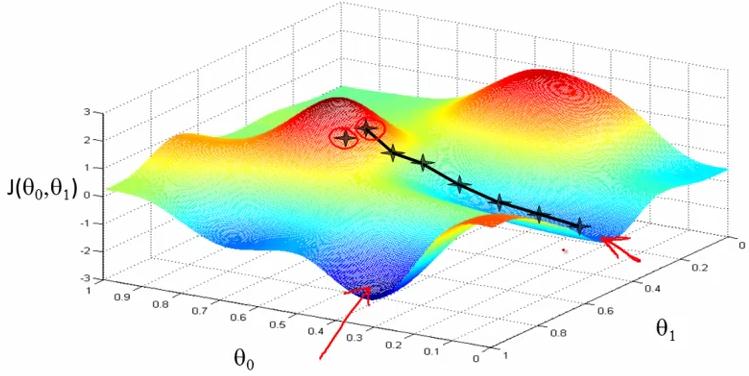
![]() (非cost function for linear regression,一般情况下的J(θ0,θ1))
(非cost function for linear regression,一般情况下的J(θ0,θ1)) - 由上图可知,不同的初始值,利用gradient descent可能得出不同的局部最优解(有不同的极小值)
大概方法步骤:
function: J(θ0,θ1)
目标: 求出J(θ0,θ1)的最小值
- 先预设 θ0,θ1的值
- 利用gradient descent反复求θ0,θ1的值
- 直至θ0,θ1的值收敛于一个确定的值(J(θ0,θ1)的极小值),(收敛是因为当到达极值时,cost function的偏导为0,这时会收敛)
- learning rate: ∂(大于0),朝着cost function的梯度方向以a(learning rate)系数倍数逼近cost function(θ0,θ1为参数)的最小值。
- learning rate太小:使求出收敛的值时迭代的次数变多,使收敛过程变慢(下图是假设θ0已知,θ1未知时的cost function图形,若都未知则图应是立体的,如上图)
![]()
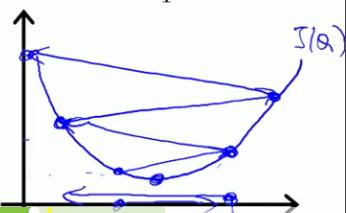
- learning rate太大:可能会导致无法收敛,得不到正确的值(下图是假设θ0已知,θ1未知时的cost function图形,若都未知则图应是立体的,如上图)
![]()
- The gradient descent equation:
![]() (j=0,1)
(j=0,1)
-
-
- :=为赋值操作,=为truth assertion操作
- 要同时更新θ0,θ1的值(update simultaneously),即算出θ0的新值后,不能利用这个新值的J(θ0,θ1)去算θ1,而是同时更新θ0,θ1
- 求的是局部最优解(即cost function的极小值,但是不是最小值)
- 但是由cost function for linear regression的图(像一个碗状)可知,它只有一个极小值(也是它的最小值),所以对于linear regression问题,gradient descent求的是cost function的最小值
-
-
-
Gradient Descent for Linear Regression:
![]() (是将h(x)=θ0+θ1x和J(θ0,θ1)代入求导求得)
(是将h(x)=θ0+θ1x和J(θ0,θ1)代入求导求得)![]()
- cost function for linear regression由它的图(上图)可知,它没有局部极小值,只有一个全局最小值。所以用gradient descent求出的是使cost function取最小值的θ0,θ1
- "batch" gradient descent = gradient descent algorithm,因为在计算θ0,θ1时是利用了所有的trainning set,帮称为batch
-

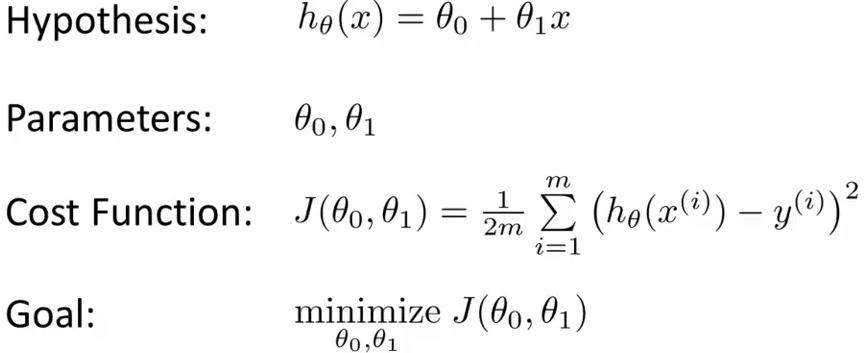
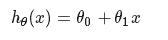 ,
,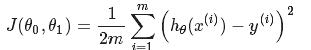 (y为真实的值),
(y为真实的值),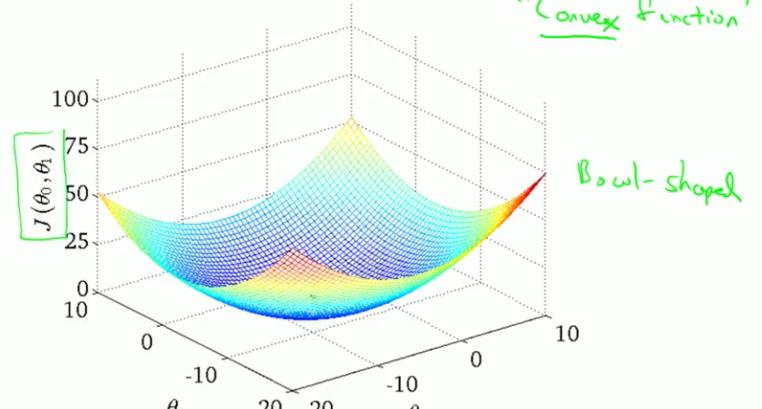
 (非cost function for linear regression,一般情况下的J(θ0,θ1))
(非cost function for linear regression,一般情况下的J(θ0,θ1))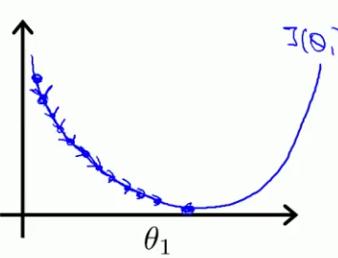
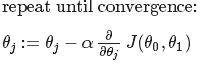 (j=0,1)
(j=0,1) 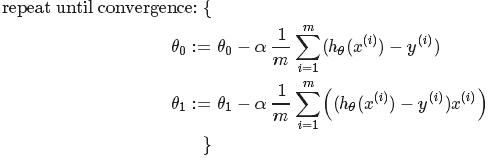 (是将h(x)=θ0+θ1x和J(θ0,θ1)代入求导求得)
(是将h(x)=θ0+θ1x和J(θ0,θ1)代入求导求得)

 浙公网安备 33010602011771号
浙公网安备 33010602011771号