吴恩达学习笔记6（logistic regression）
2023-03-06 16:54:15 星期一
接下来讨论y是离散值情况下的分类问题
逻辑回归（Logistic Regression）
分类问题举例
此时y是有两个取值的变量：0 or 1
0表示负类：没有某个东西
1表示正类：有某个东西
开发一个分类算法
eg.对肿瘤进行恶性和良性分类
1：有肿瘤
0：没有肿瘤
将线性回归算法应用到这个数据集，用直线对数据进行拟合
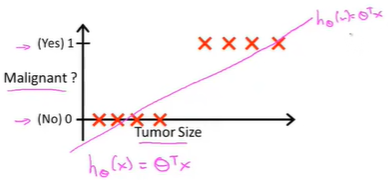
此时想做出预测，将分类器输出的阈值设为0.5，即纵坐标值为0.5
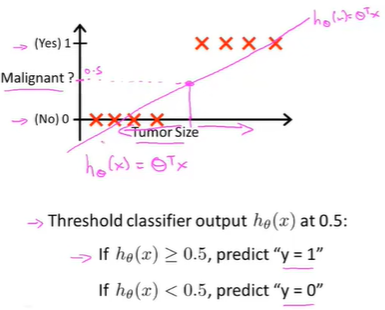
用线性回归后，在0.5这个点右边的值预测为正，左边预测为负。
延长横轴，此时有另一个训练样本
此时训练样本增加一个点，运用线性回归，会得到另一条直线去拟合数据，现在阈值设为0.5得到的预测结果就不准确(蓝色线)
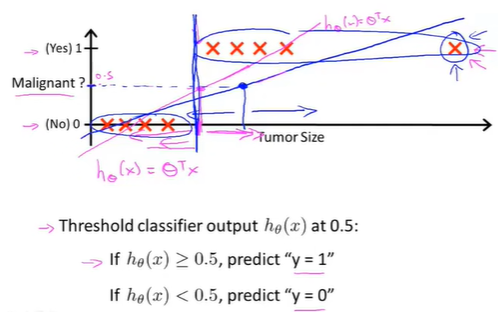
此时，数据的拟合直线从红色变成蓝色，从而生成了一个更坏的假设
So.
把线性回归应用于分类问题并不是一个好主意
把线性回归用于分类问题，会发生什么？
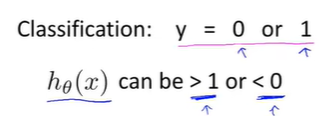
对于分类问题：y = 0 or 1
使用线性回归时假设的输出值会远大于1或远小于0，即使所有训练样本的标签都是y = 0 or 1
逻辑回归算法(logistic regression)
算法的预测或者输出值一直介于0和1之间，logistic regression是一种分类算法，而不是回归算法
假设表示（Hypothesis Representation）
当有一个分类问题的时候，我们要使用哪一个方程来表示我们的假设
回顾：我们希望分类器的输出值在0和1之间，所以提出一个假设让这些估算值在0到1之间
线性回归的假设：
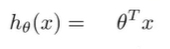
logistic 回归
假设：
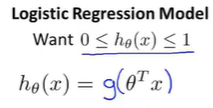
逻辑函数(losistic function or sigmoid function)：$$g(z) = \frac{1}{1+e^{-z}}$$
将上式合并得到假设的另一种形式：
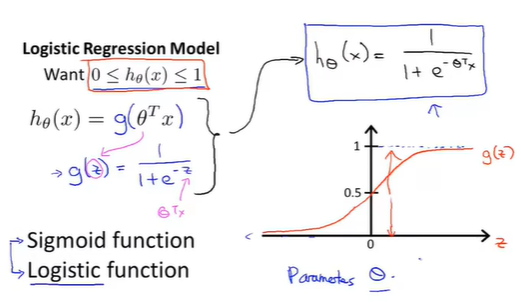
接下来，用\(\theta\)拟合数据，对于给定训练集，我们给参数\(\theta\)选定一个值
模型解释
假设\(h(x)\)的输出：
当假设输出一个数字，我们会把这个数字当作输入某个\(x\)，\(y = 1\)时的概率估计值
eg.
这个假设表示：对于一个特征为\(x\)的患者，\(y =1\)的概率是0.7，也就是70%的可能性是恶行肿瘤
写成概率形式：
表示在给定\(x\)的条件下\(y=1\)的概率，即病人特征为\(x\)的情况下，特征\(x\)也就是代表着肿瘤的大小，这个概率的参数是\(\theta\)
这里基本上是依赖假设来估计\(y=1\)的概率
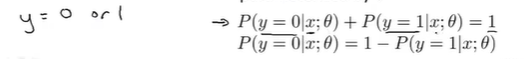
此外，由于\(y = 0\;or\; 1\)，所以根据\(h(x)\)可以估计\(y=0\)的概率；也就是因为\(y\)必须是0或1，则\(y=0\)与\(y=1\)的概率之和一定是1
决策边界(Decision boundary)
回顾：逻辑回归
To do:
这个假设函数何时会将y预测为1或0，并且更好的理解假设函数的形状,特别是有多个特征值时
要预测y等于1还是0，只要改假设函数满足下列条件即可
由\(g(z)\)的图像可以看出：
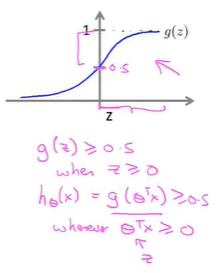
此时有
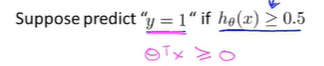
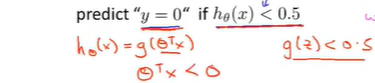
总结
要预测y的值为1还是0，取决于估值概率是大于等于0.5还是小于0.5，也就是说预测\(y=1\)只需要\(\theta^Tx\)大于或等于0，预测\(y=0\)只需要\(\theta^Tx\)小于0即可
补充：
使用sigmoid函数的意义在于将\((-\infty,+\infty)\)映射到\((0,1)\)上，映射后函数横轴小范围内变化灵敏，大范围内变化平缓
其他逻辑函数
-
决策边界（Decision boundary）
假设已经拟合好参数向量\(\theta=[-3,1,1]’\)
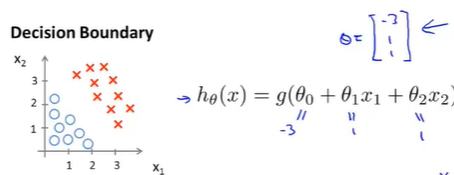
找出假设函数合适将预测\(y=1\)或\(y=0\)，由 \(y=1\) when \(\theta^Tx\geq 0\)，则
此时\(x_1+x_2=3\)将表示一条直线，图像表示为：
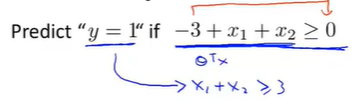
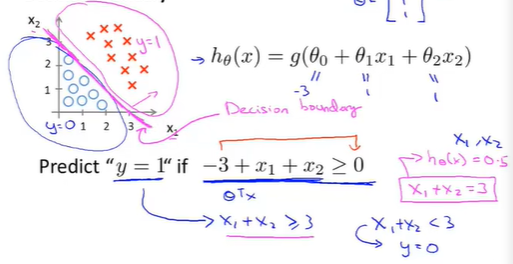
此时红色区域表示\(y=1\)，蓝色区域表示\(y=0\)；\(x_1+x_2=3\) 这条直线叫做Decision boundary，他的一系列点对应\(h(x)=0.5\)的区域
注： 决策边界是假设函数的一个属性（包括参数\(\theta_0,\theta_1,\theta_2\)），决定于其参数，它不是数据集的属性。
确定了参数就能完全确定决策边界，并不需要绘制训练集来确定决策边界 -
非线性决策边界（Non-linear decision boundary）
给定一个训练集，如何才能使用logistic回归拟合这些数据呢？对logistic回归添加额外的高阶多项式项
通过在特征中增加这些复杂的多项式，可以得到更复杂的决定边界，而不是只用直线分开正负样本
更高阶的多项式会得到更复杂的决策边界：
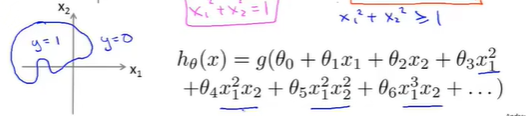
强调
决策边界不是训练集的属性，而是假设本身及其参数的属性，只要给定了参数向量\(\theta\)，圆形的决定边界就确定了。不是用训练集来定义的决策边界，而是用训练集来拟合参数\(\theta\)，参数\(\theta\)一旦确定，决策边界就确定了
