吴恩达学习笔记5 （Normal Equations）

2023-03-03 15:18:40 星期五

---

正规方程 (Normal equation with multiple variable)

对于某些线性回归问题，可以用更好的方法求得参数$\theta$的最优值

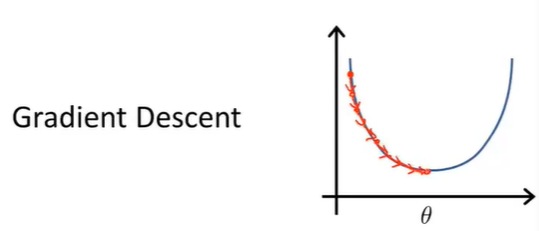
• 梯度下降算法
  经过梯度下降的多次迭代来收敛到全局最小值
  

• 正规方程法
  提供了一种求$\theta$的解析解法，不需要进行迭代运算，而是可以直接一次性求解$\theta$的最优值，基本只需要一步就能得到最优值

  $\theta$是一个标量，实数
  
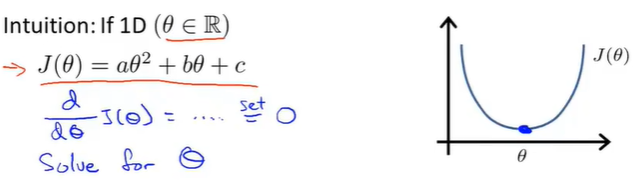
  此时最小化代价函数，对其求偏导=0时的$\theta$为最小值时的$\theta$

  $\theta$是一个n+1维的参数向量
  
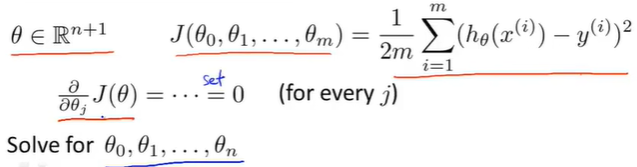
  逐个对参数${\theta }_j$求偏导，然后置0，解得${\theta }_j$的值即为最小化代价函数J的$\theta$的值

正规方程法

Example 1

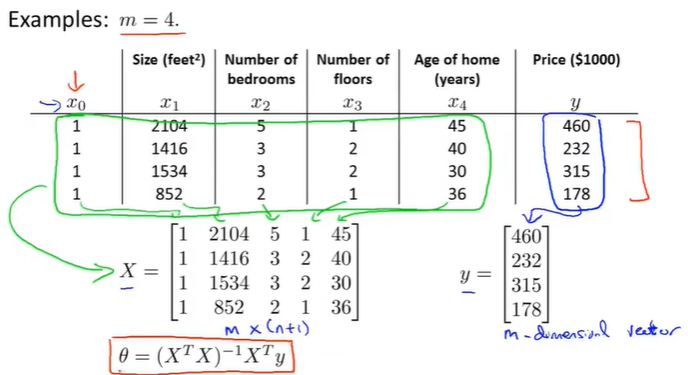
构建矩阵X，包含所有特征变量
$X^{T}X$表示X是满秩方阵，此时X可逆

Example 2

m个训练样本$(x^m,y^m)$和n个特征变量，每个训练样本$x^{(i)}$是一个n+1维的特征向量， 取每个训练样本的转置构建矩阵X

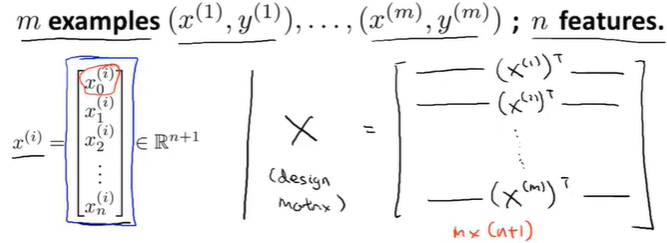
eg.

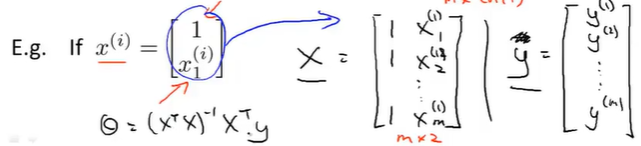
这里X写错了，改为

$$\left[\begin{array}{cc}1& x_1^{(1)}\\ 1& x_1^{(2)}\\ ...& ...\\ 1& x_1^{(m)}\end{array}\right]$$

matlab代码实现

正规方程法不需要进行特征缩放

梯度下降算法和正规方程对比

m个训练集，n个特征变量

Gradient Descent	Normal Equation
Need to choose $\alpha$	No need to choose $\alpha$
Need many iterations	Don't need to iterations
Works well even when n is large	Need to compute $(X^{T}X{)}^{-1}$(实现逆矩阵计算的代价为$O(n^3)$
	Slow if $n$ is very large

So.
如果$n$很大，选择梯度下降法，时间更快
如果$n$比较小，选择正规方程法求解参数($n⩾1000$)

随着学习算法越来越复杂(例：logistic回归算法)，正规方程算法并不使用于那些更复杂的学习算法，使用梯度下降法更合适