吴恩达学习笔记3(multiple gradient descent)

2023-03-01 17:12:27 星期三

---

使用梯度下降法处理多元线性回归

多元输入变量(multiple features)

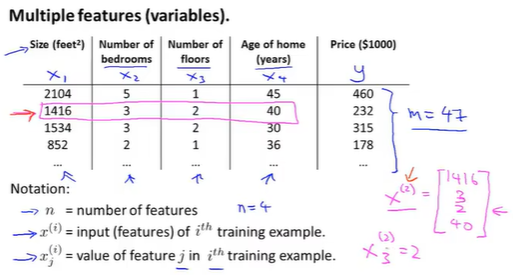
假设函数

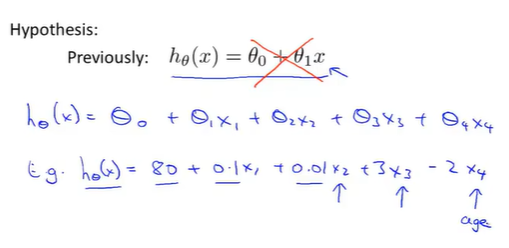
多元线性回归(multivariate linear regression)

将线性组合转换成矩阵乘法计算

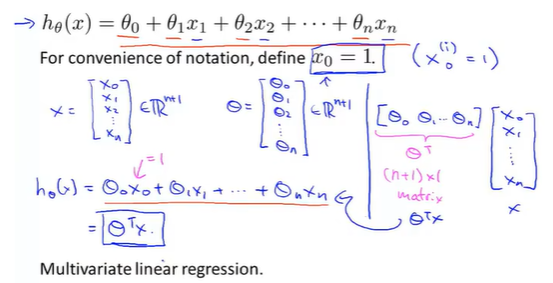
问题描述

有n+1个特征量的gradient descent

特征缩放(feature scaling)

保证多个特征在相似范围内，这样梯度下降法能够更快的收敛

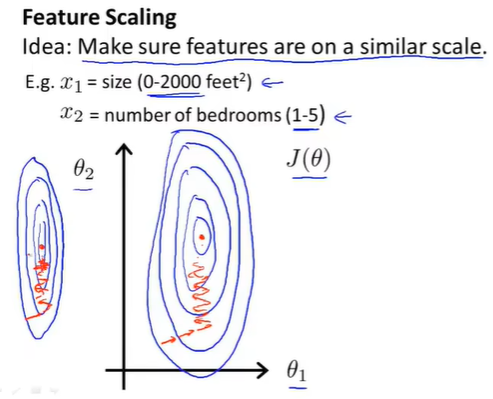
此时代价函数J的等值线图是椭圆形，梯度下降要来回波动，最终才收敛到最小值。

采用特征缩放

• 除以最大值
  $0\le x_1\le 1,0\le x_2\le 1$

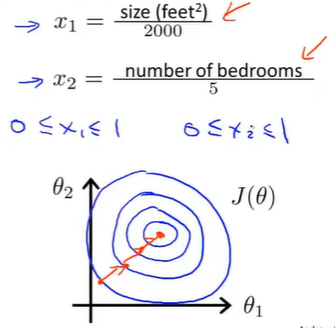
此时代价函数J的等值线偏移会变得没那么严重，此时梯度下降法是一条直线，收敛速度更快

注：
采用特征缩放时，特征取值约束到-1到+1范围内，不必严格规定，大概范围就行。

• 均值归一化
  $x_i-{\mu }_i$使特征值具有为0的平均值，然后除以最大值
  
• $x_1$可替代为

$$\frac{x_1-{\mu }_1}{s_1}$$

其中${\mu }_1$是训练集中特征$x_1$的平均值, $s_1$是该特征值的范围，即最大值-最小值（或直接用标准差代替）

梯度下降算法技巧

• 学习率（learning rate）
  

  调试以及确保梯度下降算法正确工作的小技巧
  学习率如何选

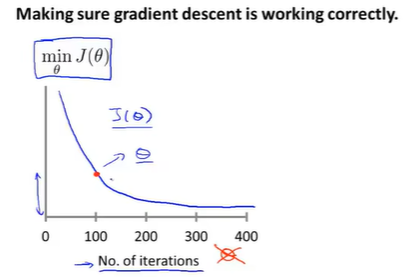
横坐标: 梯度下降算法的迭代100次
纵坐标：梯度下降算法相应100次得到的$\theta$算出的$J(\theta )$的值
表示梯度下降的每步迭代后，代价函数的值，如果梯度下降算法正常工作，每一步迭代后的$J(\theta )$都应该下降。
代价函数不继续下降==>梯度下降算法差不多已经收敛

自动收敛测试

如果$$J(\theta )<ϵ$$
此时判断函数$J(\theta )$收敛。$ϵ$可以是${10}^{-3}$，但要找到合适的阈值$ϵ$很难，因此通常通过图形来判断收敛。

不收敛情况

学习率较大

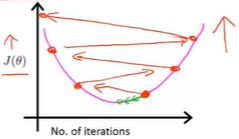
如果$J(\theta )$在上升，最常见的原因是在最小化函数时，如果学习率太大，梯度下降算法可能不断的跳过最小值，结果越来越差，就得到越来越大的$J(\theta )$值。

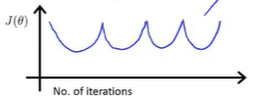
此时同样是$\alpha$太大。
学习率$\alpha$足够小，每次迭代之后代价函数$J(\theta )$都会下降。
学习率$\alpha$太小会导致梯度下降算法收敛的很慢。

总结

对于大数据样本，加速收敛就是刚开始选择大学习率，随着迭代选择小学习率。