吴恩达学习笔记2(gradient descent-)
梯度下降法(Gradient descent)
2023-02-08 14:07:53 星期三
最小线性回归的代价函数和一些其他函数
问题梗概:

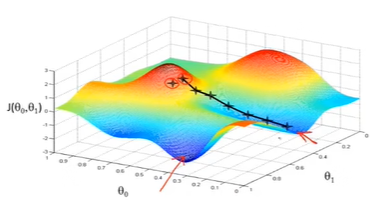
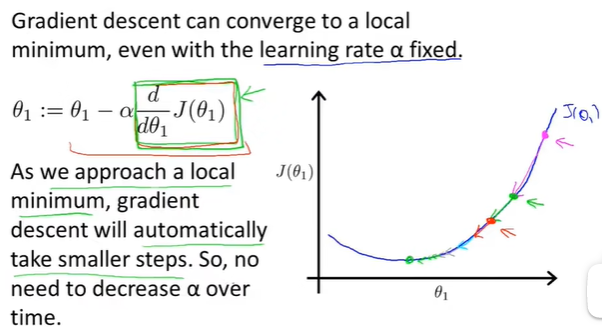
运用Gradient descent局部收敛至最低点
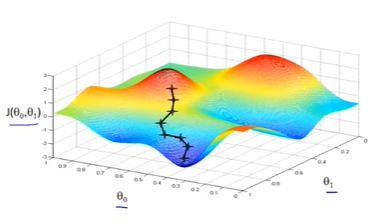
起始点不同,会得到完全不同的局部最优解
数学原理
Gradient descent algorithm
\(:=\) 表示赋值 (assignment)
\(a:=b\)表示把b赋值给a;
\(a=b\) 表示a的值等于b的值
\(\alpha\):被称作学习率 (leanring rate), 用来控制梯度下降时,迈出步子的大小(上图为例);即控制参数\(\theta_j\)的更新幅度;\(\alpha\)值越大,梯度下降越迅速,反之越缓慢

\(\theta_0,\theta_1\)是同时更新的 (simultaneously update)
先计算出右端部分存入temp0和temp1之中,然后同时更新\(\theta_0,\theta_1\)
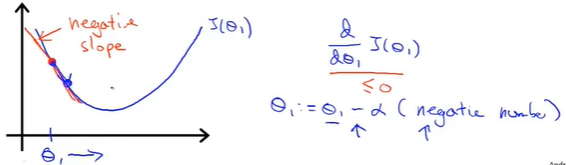
偏导\(\frac{\partial}{\partial \theta_1}\)的意义:

从\(\theta_1\)开始梯度下降
在\(\theta_1\)处的斜率为正,即\(\frac{\partial}{\partial \theta_1}\geq0\),此时\(\theta_1\)的值不断更新,向左侧移动,不断接近最小值
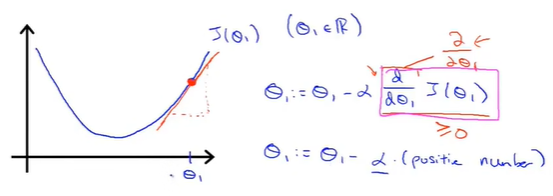
更新初始化参数\(\theta_1\)开始梯度下降
在\(\theta_1\)处的斜率为负,即\(\frac{\partial}{\partial \theta_1}\leq0\),此时\(\theta_1\)的值不断更新,向右侧移动,不断接近最小值
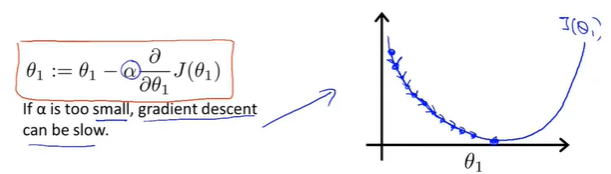
\(\alpha\)的意义:
\(\alpha\) is too small
梯度下降步数多,下降速度慢
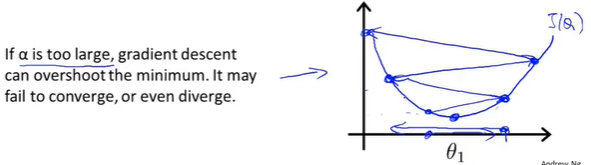
\(\alpha\) is too large
梯度下降可能会越过最低点,甚至可能无法收敛或发散
Thinking:如果\(\theta_1\)已经处在一个局部最优点,下一步梯度下降会是怎样?
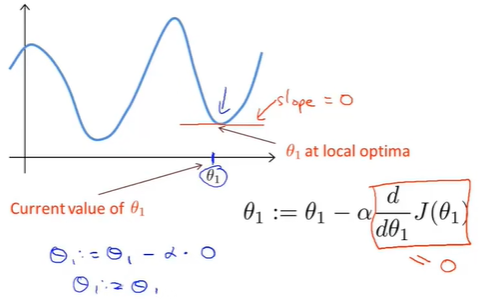
此时切线斜率为0,\(\frac{\partial}{\partial \theta_1}=0; \theta_1:= \theta_1-\alpha\cdot0\), \(\theta_1\)不发生改变,梯度下降法更新没啥用,解始终保持在局部最优解
这解释了即使learning rate\(\alpha\)保持不变,梯度下降法也可以收敛到局部最低点的原因
总结
根据定义,在局部最低值,导数为0,所以越接近最低点导数值会越来越小,梯度下降将自动采取较小的幅度,直到收敛到最优解,这就是梯度下降的运行方式
线性回归的梯度下降
用梯度下降算法求解代价函数
将梯度下降应用到最小化平方差代价函数,代码关键是写好导数部分

代价函数J对\(\theta_j\)求偏导:

其中对\(\theta_0\)求偏导得:
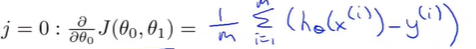
对\(\theta_1\)求偏导得:
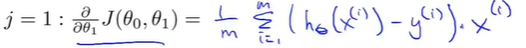
将偏导结果带入Gradient descarnt algorithm:
\(\theta_0:=\theta_0-\alpha\frac{\partial}{\partial\theta_0}J(\theta_0,\theta_1)\)
\(\theta_1:=\theta_1-\alpha\frac{\partial}{\partial\theta_1}J(\theta_0,\theta_1)\)

这就是回归的梯度下降法,不断重复上述过程直到收敛,更新\(\theta_0,\theta_1\)
梯度下降如何实现
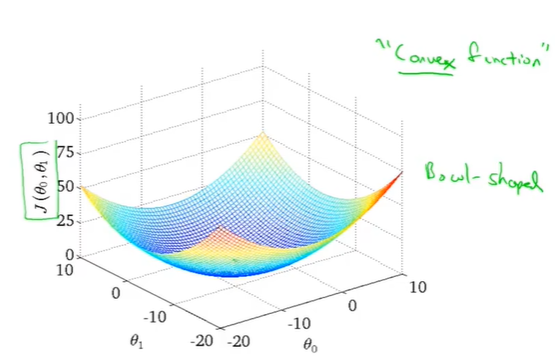
梯度下降的代价函数总是一个凸函数 (convex function)(类似一个弓形函数bowl-shaped,没有局部最优解,只有全局最优解), 使用线性回归会收敛到全局最优
Gradient descent实现过程
first point:初始化参数
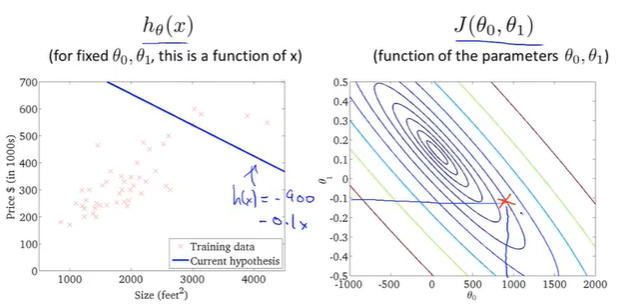
这里\(h(x)=900-0.1x\), 图中多了个负号
second point

梯度下降一步,右边代价函数点移动到新位置,左边假设函数线随之变化;
third point
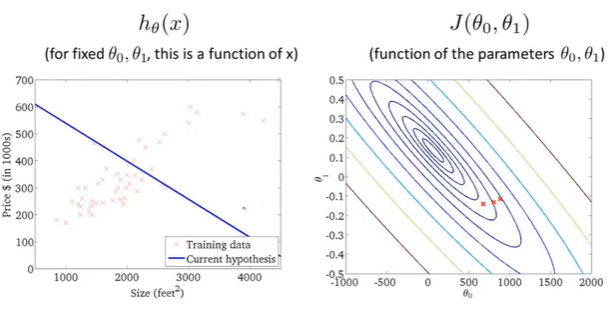
fourth point
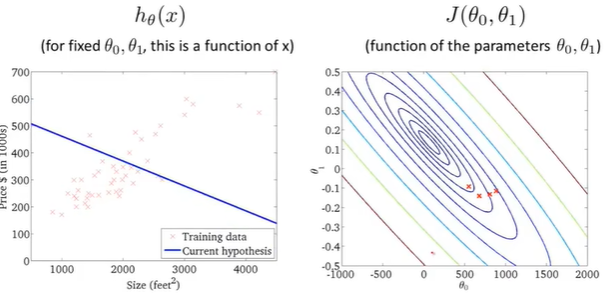
fifth point
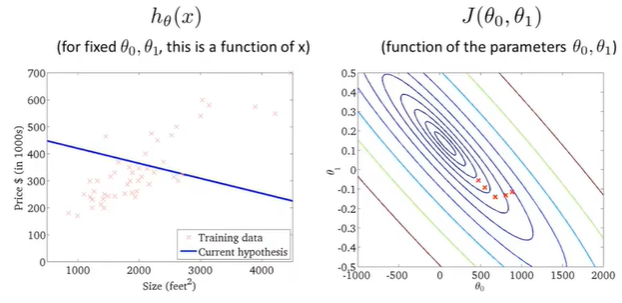
sixth point

seventh point
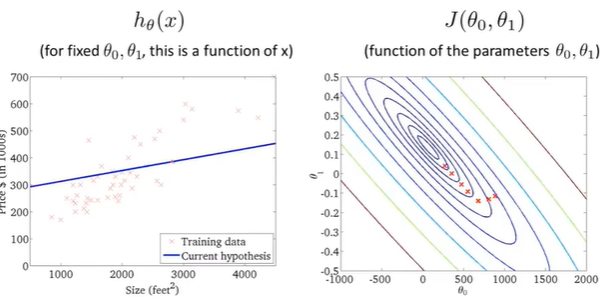
eighth point
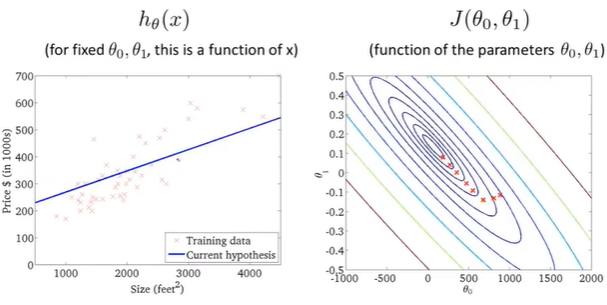
梯度下降,代价随着下降,假设函数越来越符合训练集;
ninth point
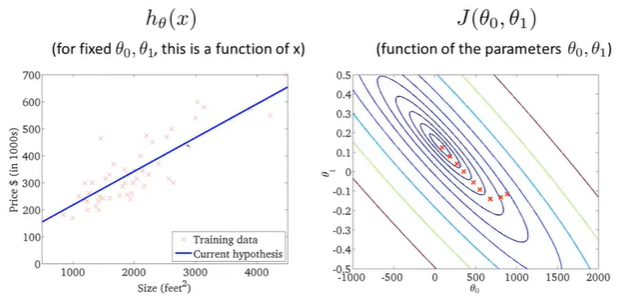
代价函数达到全局最小值,对应假设曲线很好的拟合了数据。
此时就运用梯度下降很好的拟合了训练集(房价),此时就可以用它来预测,相应面积房子的估值

总结
梯度下降算法同时被称为"Batch梯度下降":意味着每一步梯度算法都遍历了整个训练集样本,在计算导数时,先计算了每一个单独的梯度下降,然后计算m个训练样本的总和,因此Batch梯度下降全揽整个训练集。