吴恩达机器学习笔记1

2023-02-02 09:55:22 星期四

---

Supervised learning

  监督学习分为：“回归”和“分类”

Linear regression (线性回归)

例如：房价预测

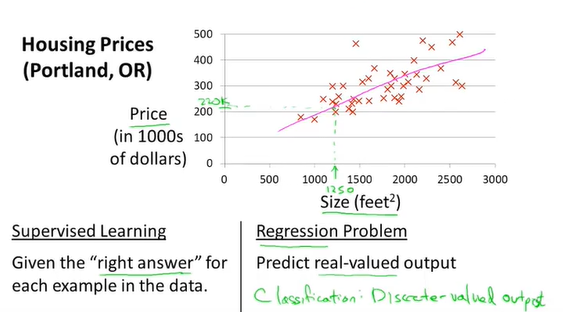
training set (训练集)

"m" 训练样本数量
"x" 表示输入变量或者说特征
"y" 表示输出变量或者说预测变量

监督学习算法如何工作

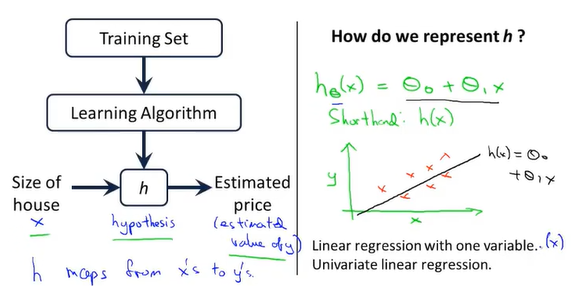
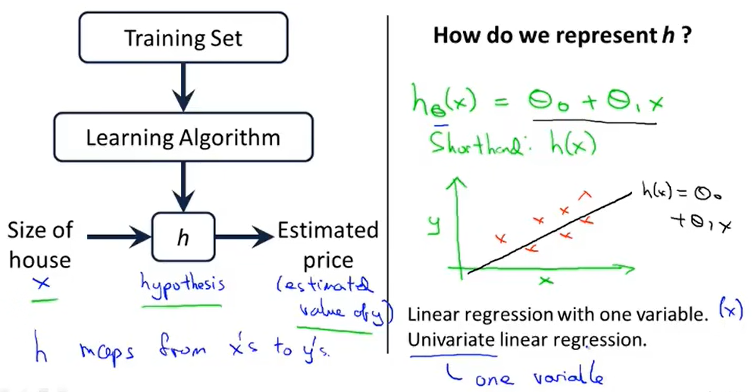
"假设函数 h" 表示一个x到y的映射
"h" 例子种是一个一元线性回归 (linear regression with one variable) 或 单变量线性回归
假设函数：
\(h = \theta _0+\theta_1x\)

代价函数 (cost function)

解决 regression problems 最常用的手段

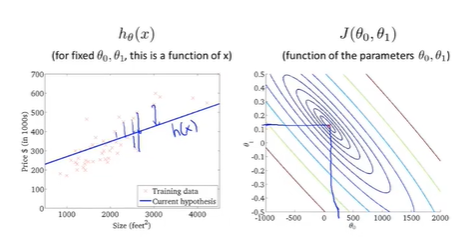
在线性回归种，有一个训练集(如图)，我们要做的就是得出假设函数中两个参数\(\theta_0\)和\(\theta_1\)的值，让假设函数表示的直线尽量的与这些数据点很好的拟合.

让我们给出标准的定义，在线性回归中要解决的是一个最小化问题
\(\mathop{minimize}\limits_{\theta_0\theta_1}\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{i})-y^{i})^2\)
m：表示训练样本个数
\(h_\theta(x^i)\): hypothesis对应的h值
\(y^i\): training set对应点的y值

cost function (square error function)
\(J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{i})-y^{i})^2\)

最小化问题变为：\(\mathop{minimize}\limits_{\theta_0\theta_1} J(\theta_0,\theta_1)\)

总结：

cost function

简化代价函数：\(\theta_0 = 0\) 以便更好理解代价函数含义

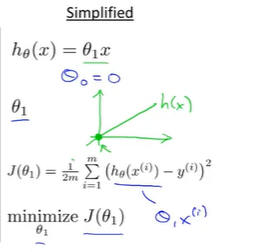
Example： 画出相应代价函数图形
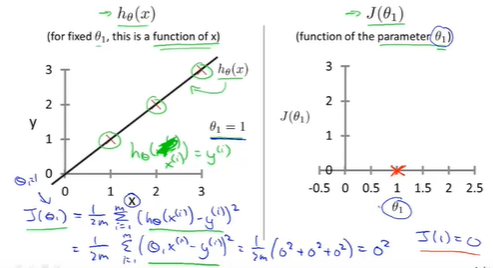
training set:(1,1),(2,2),(3,3)
hypothesis [1]: \(\theta_1 =1;h_\theta(x)=x\)

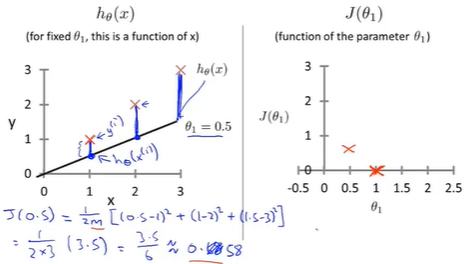
hypothesis [2]: \(\theta_1 =0.5;h_\theta(x)=0.5x\)

hypothesis [3]: \(\theta_1 =0;h_\theta(x)=0\)

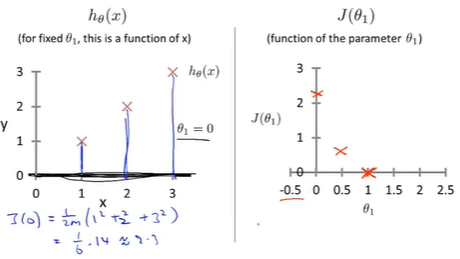
总结

最小化cost function得到最符合training set的直线，从而更好的拟合我们的training set

每个\(\theta_1\)都对应一个hypothesis(左侧)，同时得到一个对应的\(J(\theta_1)\)(右侧)。
学习算法的优化目标是通过选择的\(\theta_1\)的值，得到最小的\(J(\theta_1)\)，这是线性回归的目标函数。
\(\theta_1=1\)时，\(J(\theta_1)\)最小，得到了最符合数据的直线，此时完美的拟合了本例中的训练集。

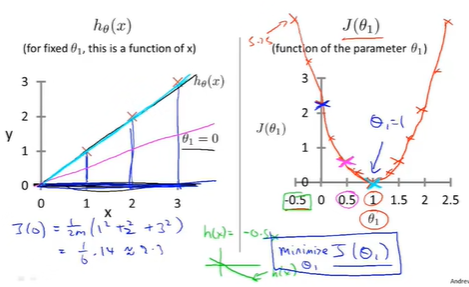
cost function (J)的意义: 对应相应假设函数，以及接近最小值的J对应着更好的假设函数