基环树小结
持续更新ing
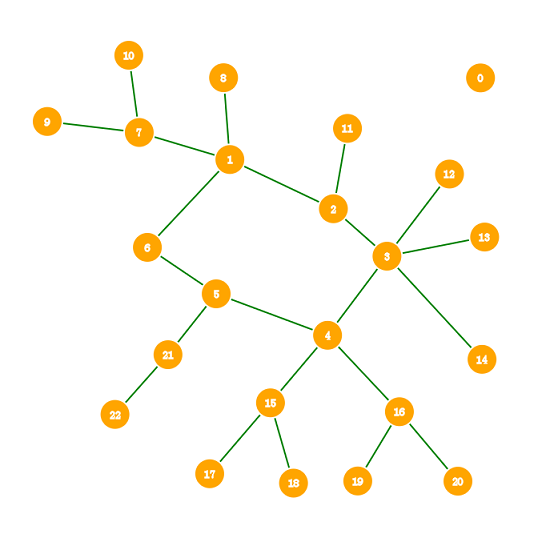
图中央的环显而易见,一般的初始化流程有两个
(1)找环
void Get_ring(LL u,LL fa){
visit[u]=++cnt;
for(LL i=head[u];i;i=dis[i].next){
LL v=dis[i].to;
if(v==fa)
continue;
if(visit[v]){
if(visit[v]<visit[u])
continue;
a[++num]=v;
f[v]=true;
for(;v!=u;v=pre[v]){
a[++num]=pre[v];
f[pre[v]]=true;
}
}else{
pre[v]=u;
Get_ring(v,u);
}
}
}
(2)找边
void Get_edge(LL u,LL now){
if(now==num+1)
return;
for(LL i=head[u];i;i=dis[i].next){
LL v=dis[i].to;
if(v!=a[now+1])
continue;
eval[now]=dis[i].d;
Get_edge(v,now+1);
}
}
题目大意:删掉一条边,在保持联通性的基础上求最小直径
既然要保持连通性,就只能考虑在环上删边
先将环中的每个节点子树最大直径求出(不跨过环)
LL Get_d(LL u,LL fa){
LL stmp=0;
for(LL i=head[u];i;i=dis[i].next){
LL v=dis[i].to;
if(v==fa||f[v])
continue;
stmp=MAX(stmp,Get_d(v,u));
LL now=first[v]+dis[i].d;
if(now>first[u]){
second[u]=first[u];
first[u]=now;
}else if(now>second[u])
second[u]=now;
}
stmp=MAX(stmp,first[u]+second[u]);
return stmp;
}
for(LL i=1;i<=num;++i)
mx[i]=Get_d(a[i],0);
以上均为初始化,下面才是难点
易证基环树的直径为 max{ 环上点子树直径与,跨环部分+左右端点直径和 }
利用环的性质又可分为越过1-n与不越过1-n分别计算
LL stmp=0;
for(LL i=1;i<num;++i){
s0[i]=MAX(s0[i-1],stmp+first[a[i]]);
stmp+=eval[i];
}
stmp=0;
for(LL i=num;i>1;--i){
s1[i]=MAX(s1[i+1],stmp+first[a[i]]);
stmp+=eval[i-1];
}
stmp=0;
for(LL i=1;i<=num;++i){
t0[i]=MAX(t0[i-1],MAX(mx[i],stmp+first[a[i]]));
stmp=MAX(stmp,first[a[i]]);
stmp+=eval[i];
}
stmp=0;
for(LL i=num;i>=1;--i){
t1[i]=MAX(t1[i+1],MAX(mx[i],stmp+first[a[i]]));
stmp=MAX(stmp,first[a[i]]);
stmp+=eval[i-1];
}
My complete code:
#include<cstdio>
using namespace std;
typedef long long LL;
const LL maxn=400000;
struct node{
LL to,next,d;
}dis[maxn*2];
LL n,num,cnt,ans;
LL head[maxn],a[maxn],eval[maxn],visit[maxn],pre[maxn],s0[maxn],s1[maxn],t0[maxn],t1[maxn],mx[maxn],first[maxn],second[maxn];
bool f[maxn];
inline void add(LL u,LL v,LL d){
dis[++num]=(node){v,head[u],d}; head[u]=num;
}
inline LL MAX(LL g1,LL g2){
return g1>=g2?g1:g2;
}
inline LL MIN(LL g1,LL g2){
return g1<=g2?g1:g2;
}
void Get_ring(LL u,LL fa){
visit[u]=++cnt;
for(LL i=head[u];i;i=dis[i].next){
LL v=dis[i].to;
if(v==fa)
continue;
if(visit[v]){
if(visit[v]<visit[u])
continue;
a[++num]=v;
f[v]=true;
for(;v!=u;v=pre[v]){
a[++num]=pre[v];
f[pre[v]]=true;
}
}else{
pre[v]=u;
Get_ring(v,u);
}
}
}
void Get_edge(LL u,LL now){
if(now==num+1)
return;
for(LL i=head[u];i;i=dis[i].next){
LL v=dis[i].to;
if(v!=a[now+1])
continue;
eval[now]=dis[i].d;
Get_edge(v,now+1);
}
}
LL Get_d(LL u,LL fa){
LL stmp=0;
for(LL i=head[u];i;i=dis[i].next){
LL v=dis[i].to;
if(v==fa||f[v])
continue;
stmp=MAX(stmp,Get_d(v,u));
LL now=first[v]+dis[i].d;
if(now>first[u]){
second[u]=first[u];
first[u]=now;
}else if(now>second[u])
second[u]=now;
}
stmp=MAX(stmp,first[u]+second[u]);
return stmp;
}
inline void init(){
scanf("%lld",&n);
for(LL i=1;i<=n;++i){
LL u,v,d;
scanf("%lld%lld%lld",&u,&v,&d);
add(u,v,d);
add(v,u,d);
}
}
inline void solve(){
num=0;
Get_ring(1,0);
a[num+1]=a[1];
Get_edge(a[1],1);
for(LL i=1;i<=num;++i)
mx[i]=Get_d(a[i],0);
LL stmp=0;
for(LL i=1;i<num;++i){
s0[i]=MAX(s0[i-1],stmp+first[a[i]]);
stmp+=eval[i];
}
stmp=0;
for(LL i=num;i>1;--i){
s1[i]=MAX(s1[i+1],stmp+first[a[i]]);
stmp+=eval[i-1];
}
stmp=0;
for(LL i=1;i<=num;++i){
t0[i]=MAX(t0[i-1],MAX(mx[i],stmp+first[a[i]]));
stmp=MAX(stmp,first[a[i]]);
stmp+=eval[i];
}
stmp=0;
for(LL i=num;i>=1;--i){
t1[i]=MAX(t1[i+1],MAX(mx[i],stmp+first[a[i]]));
stmp=MAX(stmp,first[a[i]]);
stmp+=eval[i-1];
}
ans=t0[num];
for(LL i=1;i<num;++i)
ans=MIN(ans,MAX(MAX(t0[i],t1[i+1]),s0[i]+s1[i+1]+eval[num]));
}
int main(){
init();
solve();
printf("%lld",ans);
return 0;
}


