关于几何的一点高中知识

弧度

先来认识一下弧度，在半径为\(r\)的圆上一个扇形，\(\angle\alpha\)，其弧长为\(\ell\)，则\(\angle \alpha=\frac{\ell}{r}\)

而一个圆周角的弧度为\(\frac{\ell}{r}=\frac{2\pi r}{r}=2\pi\)

弧度的单位为\(rad\)，但通常后面不需要带单位

\(sin~1=sin~1rad,sin 1≠sin 1^o\)

向量

移动向量是不会改变大小的

• \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{BC}\)

• \(\overrightarrow{AB}-\overrightarrow{AC}=-\overrightarrow{AC}+\overrightarrow{AB}=\overrightarrow{CB}\)
  向量取负相当于大小不变，方向相反，就形成了\(C-A-B\)的路线，由于向量加法是带有首尾相连性质的，所以结果显然

• \(\vec{a}\cdot \vec{b}=(x_1,y_1)\cdot (x_2,y_2)\)：我们可以看作模长乘投影

\(|a|\cdot |b|\cdot cos~\alpha\)：

\(x_1x_2+y_1y_2\)：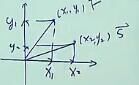

来证明一下这个：

\[\begin{aligned} (x_1,y_1)\cdot (x_2,y_2)&=(x_1\vec{e_1}+y_1\vec{e_2})(x_2\vec{e_1}+y_2\vec{e_2})\\ &=x_1x_2\vec{e_1}^2+(x_1y_2+y_1x_2)\vec{e_1}\vec{e_2}+y_1y_2\vec{e_2}^2\\ &=x_1x_2+y_1y_2\end{aligned}\]

三角函数

\(r\)是线段的长度，为正数，而\(x\)为坐标，当\(\alpha>90^o\)，\(x\)为负数，\(cos(\alpha)<0\)

\(cos(\pi)=-1\)，利用反函数得\(\pi=acos(-1)\),\(cos(0)=1\)

诱导公式

诱导公式的两部分：

旋转特殊角同一函数值的变化：正负取决于旋转后的两边比中的两边相对于之前的正负变化，同正异负

• \(cos/sin/tan(\alpha)=(\alpha+2k\pi)\)

• \(cos/sin(\alpha)=-(\alpha+\pi),tan(\alpha)=(\alpha+\pi)\)

• \(-\alpha\)为\(\alpha\)的终边关于\(x\)轴对称，那么\(y_2=-y_1\)
  \(sin/tan(\alpha)=-(-\alpha),cos(\alpha)=(-\alpha)\)

• \(\pi -\alpha\)为\(\alpha\)的终边关于\(y\)轴对称，类似于上面，不再赘述

一个三角函数通过\(x\)值的变化转换到另一个函数

• \(sin(\frac{\pi}{2}-\alpha)=cos(\alpha),cos(\frac{\pi}{2}-\alpha)=sin(\alpha)\)：\(\frac{\pi}{2}-\alpha+\alpha=\frac{\pi}{2}\)，所以终边关于\(y=x\)对称，横纵坐标刚好交换了

• \(sin(\frac{\pi}{2}+\alpha)=cos(\alpha),cos(\frac{\pi}{2}+\alpha)=-sin(\alpha)\)：终边关于\(x\)轴对称，\((x,y)\longrightarrow(-y,x)\)

余弦公式

\(cos(\alpha+\beta)=cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)\)，\(cos(\alpha-\beta)=cos(\alpha)cos(\beta)+sin(\alpha)sin(\beta)\)